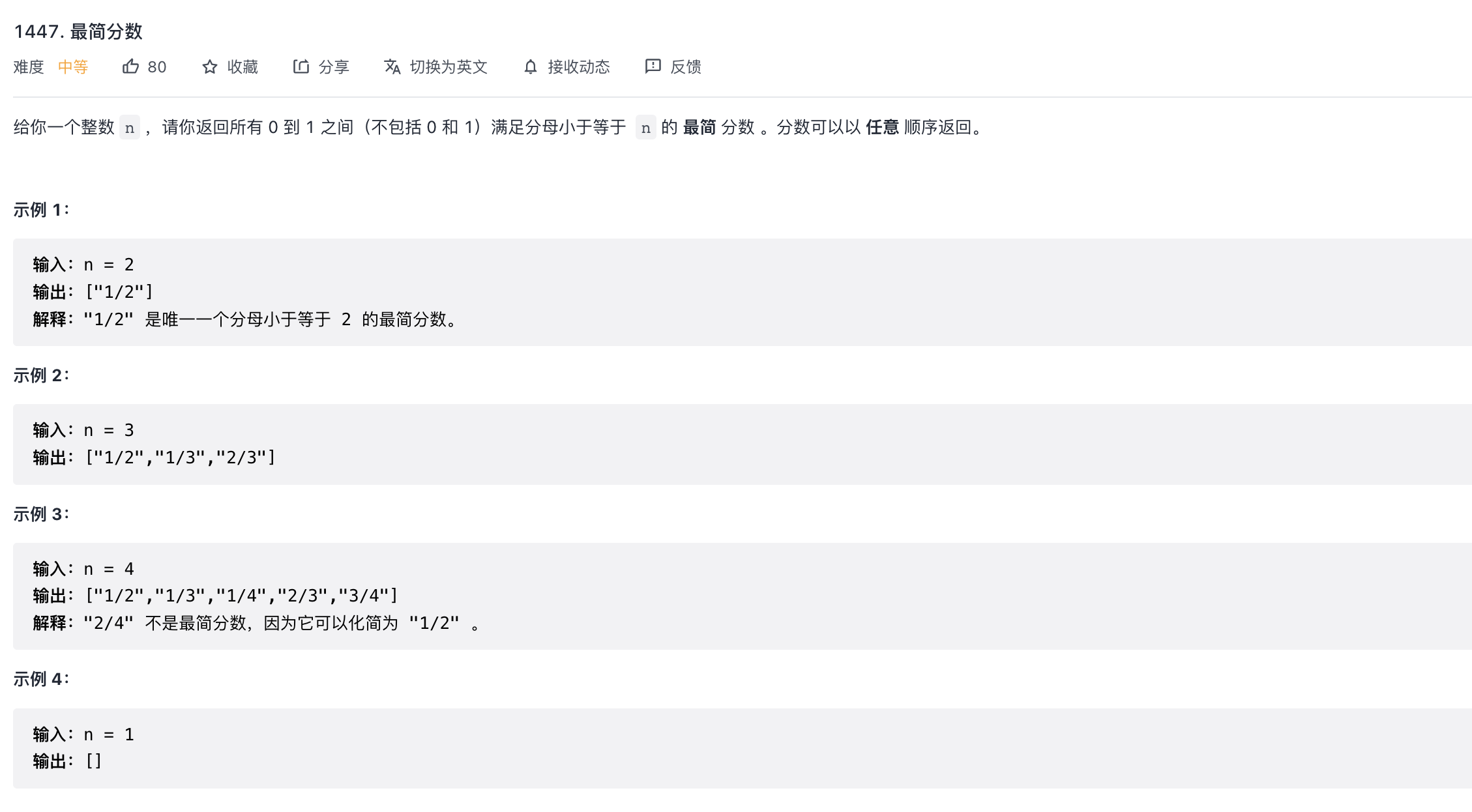
题目

类型：数学

解题思路

数据范围为 100 且数值大小在 (0, 1) 之间，因此枚举「分子 + 分母」的 做法是可接受的。
于是问题转化为：如何快速判断两个数组成的分数是否为最简（即判断两个数的最大公约数是否为 1）。
快速求得 a 和 b 的最大公约数的主要方式有两种 :
「更相减损法」和「欧几里得算法」，其中「欧几里得算法」的递归实现最为好写，复杂度为 ，在绝大多数的情况下适用，只有在需要实现高精度时，才会考虑使用「更相减损法」。
而 stein 算法则是没有必要掌握的。

代码

class Solution {
    int gcd(int a, int b) { // 欧几里得算法
        return b == 0 ? a : gcd(b, a % b);
    }
    public List<String> simplifiedFractions(int n) {
        List<String> ans = new ArrayList<>();
        for (int i = 1; i < n; i++) {
            for (int j = i + 1; j <= n; j++) {
                if (gcd(i, j) == 1) ans.add(i + "/" + j);
            }
        }
        return ans;
    }
}