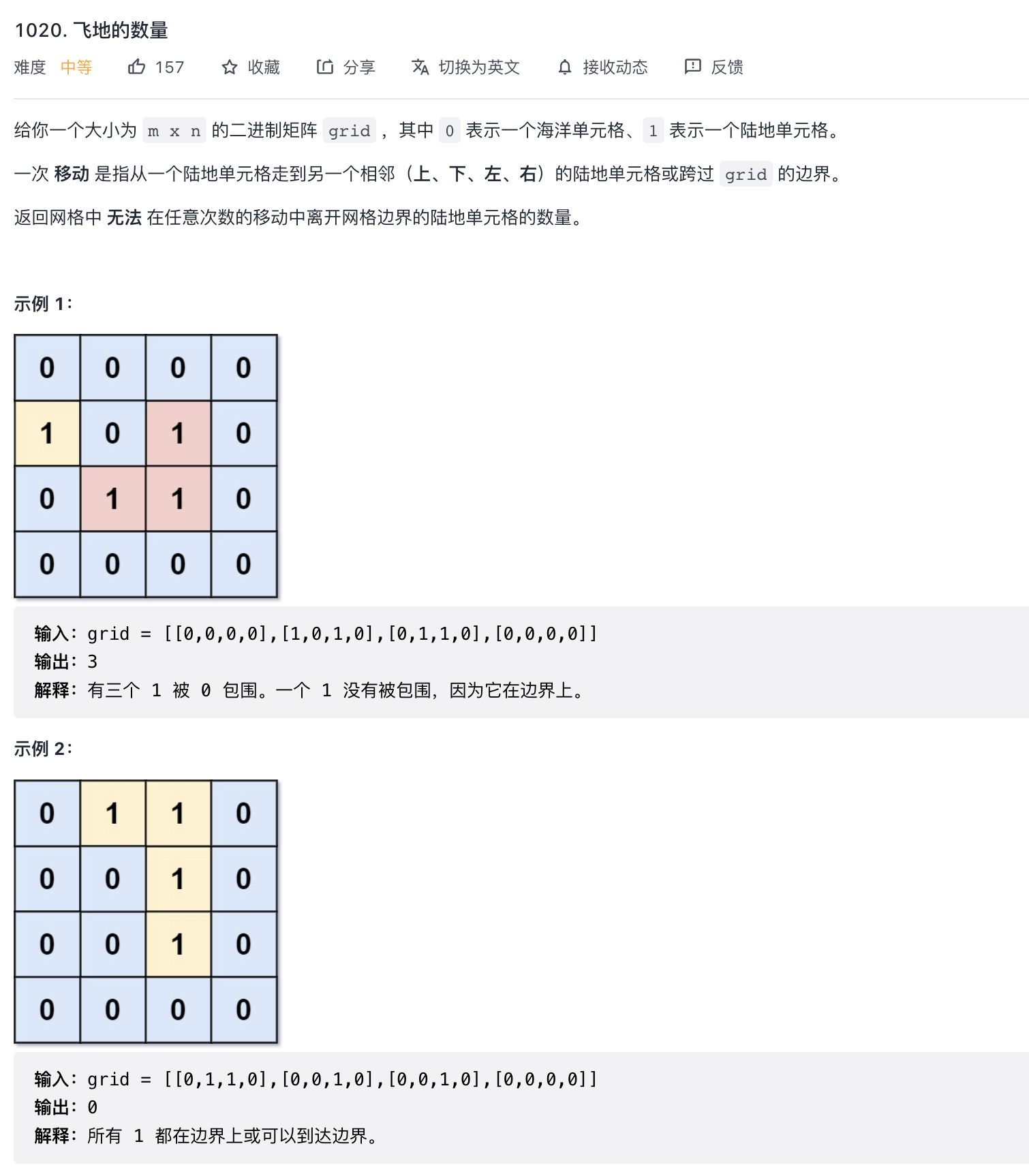
题目

类型：DFS

解题思路

根据题目定义，我们知道需要统计所有不和「边缘陆地」相连通的「普通陆地」数量。

我们可以用「并查集」来维护连通块，使用 DFS 对所有「边缘陆地连通块」进行标记（设定编号为 0 的超级源点，对于所有的「边缘陆地连通块」，将其与超级源点联通）。

具体的，我们按照如下流程进行处理：

• 初始化并查集：起始让每个单元格独立作为一个连通块；
• 使用 DFS 标记所有「边缘陆地连通块」：从位于边缘的「边缘陆地」进行出发，将其所在连通块与超级源点 0 进行联通标记（同时为了确保复杂度，我们在进行 DFS 前需要先检查当前陆地与超级源点的联通关系，如果已联通，说明当前陆地棣属于之前的某个连通块，已被整体标记过，进行跳过即可）；
• 统计答案：遍历整个棋盘，统计所有不与超级源点 0 联通的陆地数量。

一些细节：由于我们人为规定了超级源点编号为 0，同时棋盘下标从 0 开始，因此对某个点 (x, y) 的编号，我们需要增加一个偏移量，例如 idx = x * n + y + 1。

代码

class Solution {
    public int numEnclaves(int[][] g) {
        int m = g.length, n = g[0].length;
        boolean[][] vis = new boolean[m][n];
        Deque<int[]> d = new ArrayDeque<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0 || i == m - 1 || j == n - 1) {
                    if (g[i][j] == 0) continue;
                    vis[i][j] = true;
                    d.addLast(new int[]{i, j});
                }
            }
        }
        int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
        while (!d.isEmpty()) {
            int[] poll = d.pollFirst();
            int x = poll[0], y = poll[1];
            for (int[] di : dirs) {
                int nx = x + di[0], ny = y + di[1];
                if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                if (g[nx][ny] != 1) continue;
                if (vis[nx][ny]) continue;
                vis[nx][ny] = true;
                d.addLast(new int[]{nx, ny});
            }
        }
        int ans = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (g[i][j] == 1 && !vis[i][j]) ans++;
            }
        }
        return ans;
    }
}