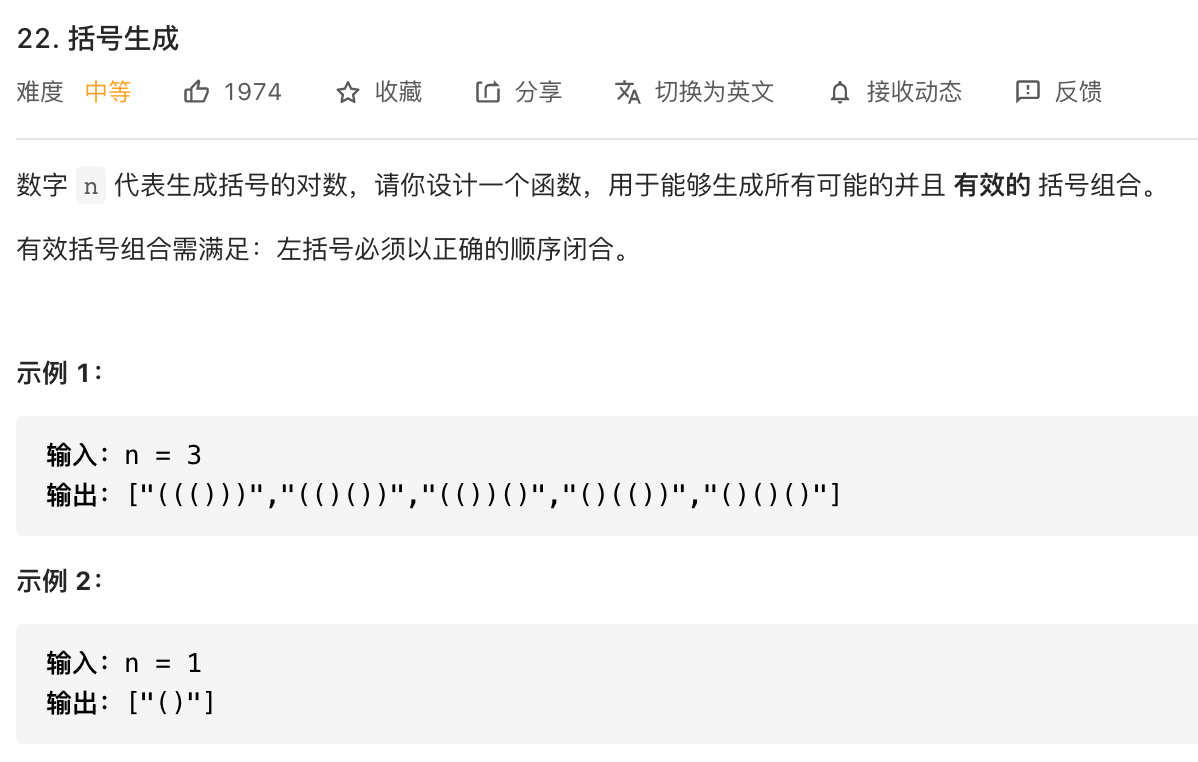
题目

类型：动态规划

难度：中等

解题思路

1、任何一个括号序列都一定是由 ( 开头，并且第一个 ( 一定有一个唯一与之对应的 )。这样一来，每一个括号序列可以用 (a)b 来表示，其中 a 与 b 分别是一个合法的括号序列（可以为空）。

2、要生成所有长度为 2 * n 的括号序列，定义一个函数 generate(n) 来返回所有可能的括号序列。那么在函数 generate(n) 的过程中：

• 枚举与第一个 ( 对应的 ) 的位置 2 * i + 1；
• 递归调用 generate(i) 即可计算 a 的所有可能性；
• 递归调用 generate(n - i - 1) 即可计算 b 的所有可能性；
• 遍历 a 与 b 的所有可能性并拼接，即可得到所有长度为 2 * n 的括号序列。

在每次 generate(i) 函数返回之前，把返回值存储起来，下次再调用 generate(i) 时可以直接返回，不需要再递归计算。

代码

class Solution {
    ArrayList[] cache = new ArrayList[100];
    public List<String> generate(int n) {
        if (cache[n] != null) {
            return cache[n];
        }
        ArrayList<String> ans = new ArrayList<String>();
        if (n == 0) {
            ans.add("");
        } else {
            for (int c = 0; c < n; ++c) {
                for (String left: generate(c)) {
                    for (String right: generate(n - 1 - c)) {
                        ans.add("(" + left + ")" + right);
                    }
                }
            }
        }
        cache[n] = ans;
        return ans;
    }
    public List<String> generateParenthesis(int n) {
        return generate(n);
    }
}