题目

类型：动态规划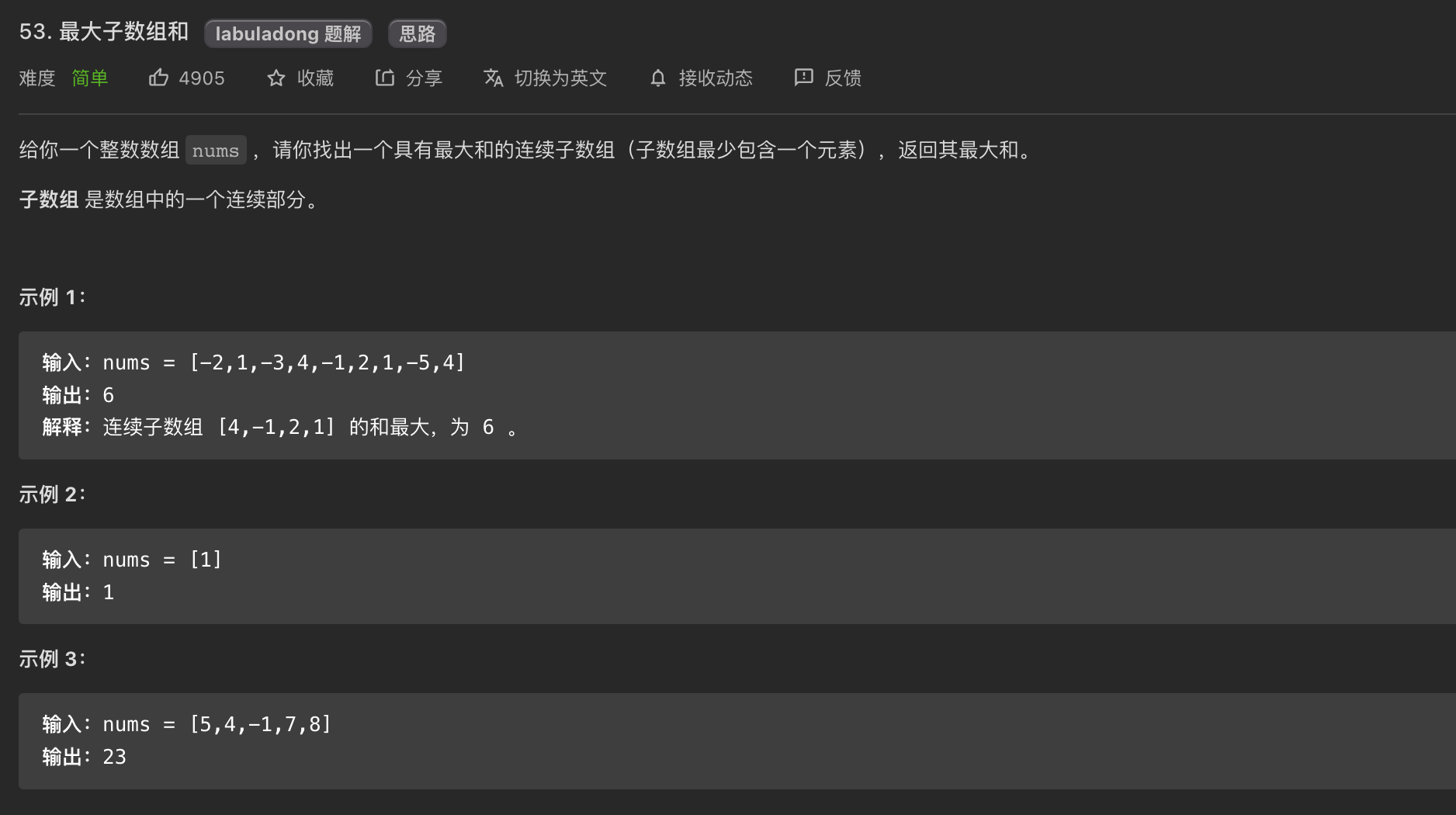

解题思路

因为子数组一定是连续的，并不能保证 nums[0..i] 中的最大子数组与 nums[i+1] 是相邻的，也就没办法从 dp[i] 推导出 dp[i+1]。
依然使用数学归纳法来找状态转移关系：假设我们已经算出了 dp[i-1]，如何推导出 dp[i] 呢？
可以做到，dp[i] 有两种「选择」，要么与前面的相邻子数组连接，形成一个和更大的子数组；要么不与前面的子数组连接，自成一派，自己作为一个子数组。
如何选择？既然要求「最大子数组和」，当然选择结果更大的那个啦：

// 要么自成一派，要么和前面的子数组合并
dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);

综上，我们已经写出了状态转移方程，就可以直接写出解法了：

int maxSubArray(int[] nums) {
    int n = nums.length;
    if (n == 0) return 0;
    // 定义：dp[i] 记录以 nums[i] 为结尾的「最大子数组和」
    int[] dp = new int[n];
    // base case
    // 第一个元素前面没有子数组
    dp[0] = nums[0];
    // 状态转移方程
    for (int i = 1; i < n; i++) {
        dp[i] = Math.max(nums[i], nums[i] + dp[i - 1]);
    }
    // 得到 nums 的最大子数组
    int res = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        res = Math.max(res, dp[i]);
    }
    return res;
}

以上解法时间复杂度是 O(N)，空间复杂度也是 O(N)，较暴力解法已经很优秀了，不过注意到 dp[i] 仅仅和 dp[i-1] 的状态有关，那么我们可以施展前文 动态规划的降维打击：空间压缩技巧 讲的技巧进行进一步优化，将空间复杂度降低：

int maxSubArray(int[] nums) {
    int n = nums.length;
    if (n == 0) return 0;
    // base case
    int dp_0 = nums[0];
    int dp_1 = 0, res = dp_0;
    for (int i = 1; i < n; i++) {
        // dp[i] = max(nums[i], nums[i] + dp[i-1])
        dp_1 = Math.max(nums[i], nums[i] + dp_0);
        dp_0 = dp_1;
        // 顺便计算最大的结果
        res = Math.max(res, dp_1);
    }
    return res;
}

代码

class Solution {
    public int maxSubArray(int[] nums) {
        int pre = 0, maxAns = nums[0];
        for (int x : nums) {
            pre = Math.max(pre + x, x);
            maxAns = Math.max(maxAns, pre);
        }
        return maxAns;
    }
}