题目

类型：BFS

解题思路

「单源最短路」问题：本质是在一个边权为 的图上，求从特定「源点」出发到达特定「汇点」的最短路径。
与「单源最短路」不同，「多源最短路」问题是求从「多个源点」到达「一个/多个汇点」的最短路径。通过建立「虚拟源点」的方式，我们可以「多源 BFS」转换回「单源 BFS」问题。

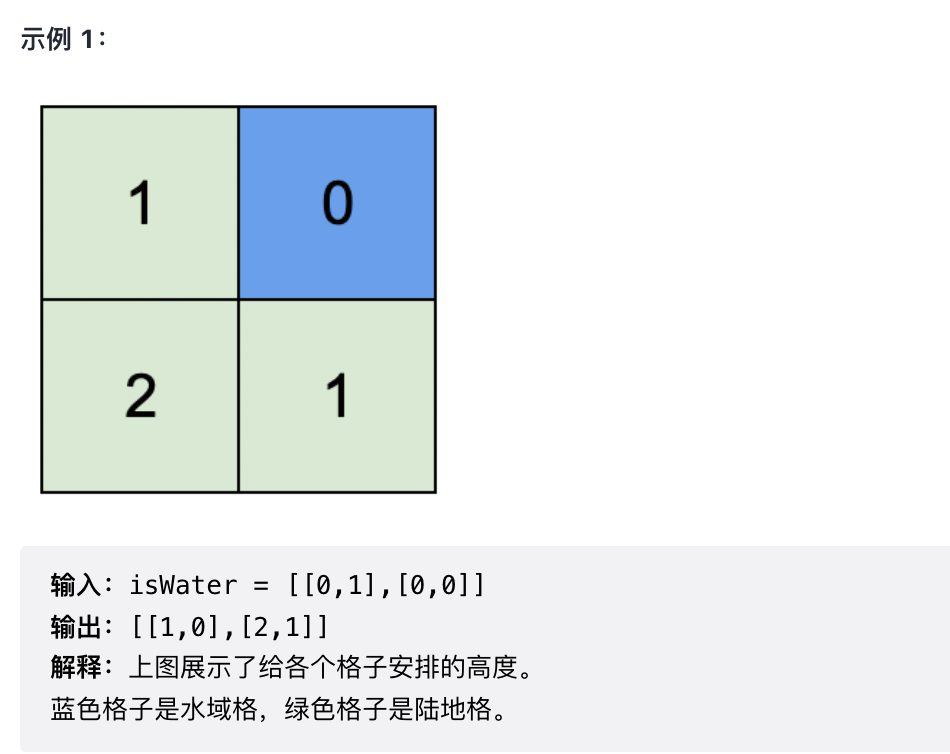
题目规定了水域区域的高度为 0，然后相邻格子之间的高度差至多为 1，可以将所有水域（高度为 0）区域进行入队，然后跑一遍 BFS 即可。
将所有水域（高度为 0）区域进行入队的操作可看作是将与「虚拟源点」链接的节点进行入队（也等价于起始只将虚拟源点入队）：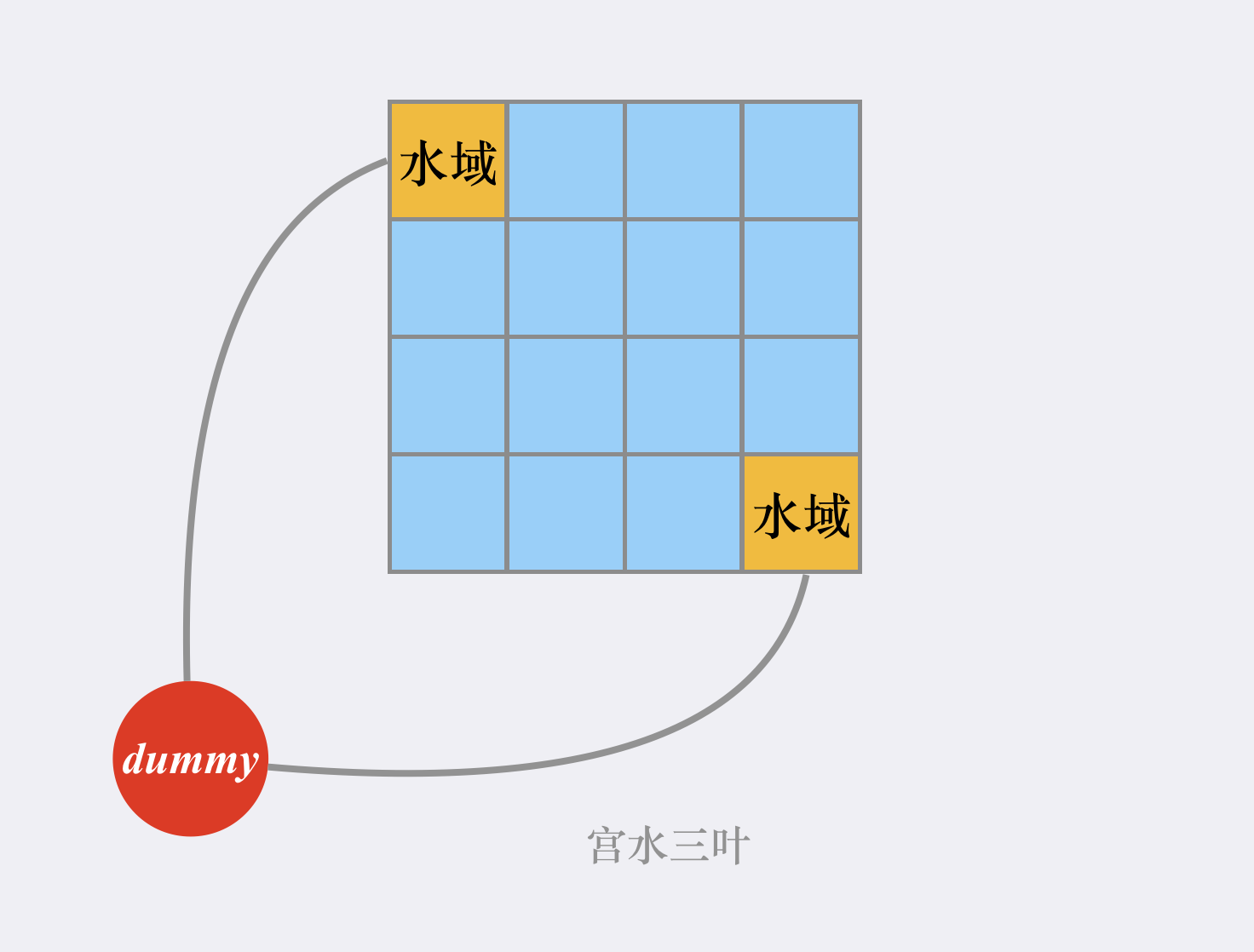

对于一个「陆地」区域（高度可变）而言，其所能填入的高度，取决于其距离其他「水域」区域的距离，而我们最终要让整个答案矩阵合法，因此每个「陆地」区域应该取其所能填入的高度的「下界」，即只由「距离它最近的水域」区域所更新，这符合 BFS 的性质

代码

class Solution {
    public int[][] highestPeak(int[][] g) {
        int m = g.length, n = g[0].length;
        int[][] ans = new int[m][n];
        Deque<int[]> d = new ArrayDeque<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (g[i][j] == 1) d.addLast(new int[]{i, j});
                ans[i][j] = g[i][j] == 1 ? 0 : -1;
            }
        }
        int[][] dirs = new int[][]{{1,0}, {-1,0}, {0,1}, {0,-1}};
        int h = 1;
        while (!d.isEmpty()) {
            int size = d.size();
            while (size-- > 0) {
                int[] info = d.pollFirst();
                int x = info[0], y = info[1];
                for (int[] di : dirs) {
                    int nx = x + di[0], ny = y + di[1];
                    if (nx < 0 || nx >= m || ny < 0 || ny >= n) continue;
                    if (ans[nx][ny] != -1) continue;
                    ans[nx][ny] = h;
                    d.addLast(new int[]{nx, ny});
                }
            }
            h++;
        }
        return ans;
    }
}