题目

类型：哈希表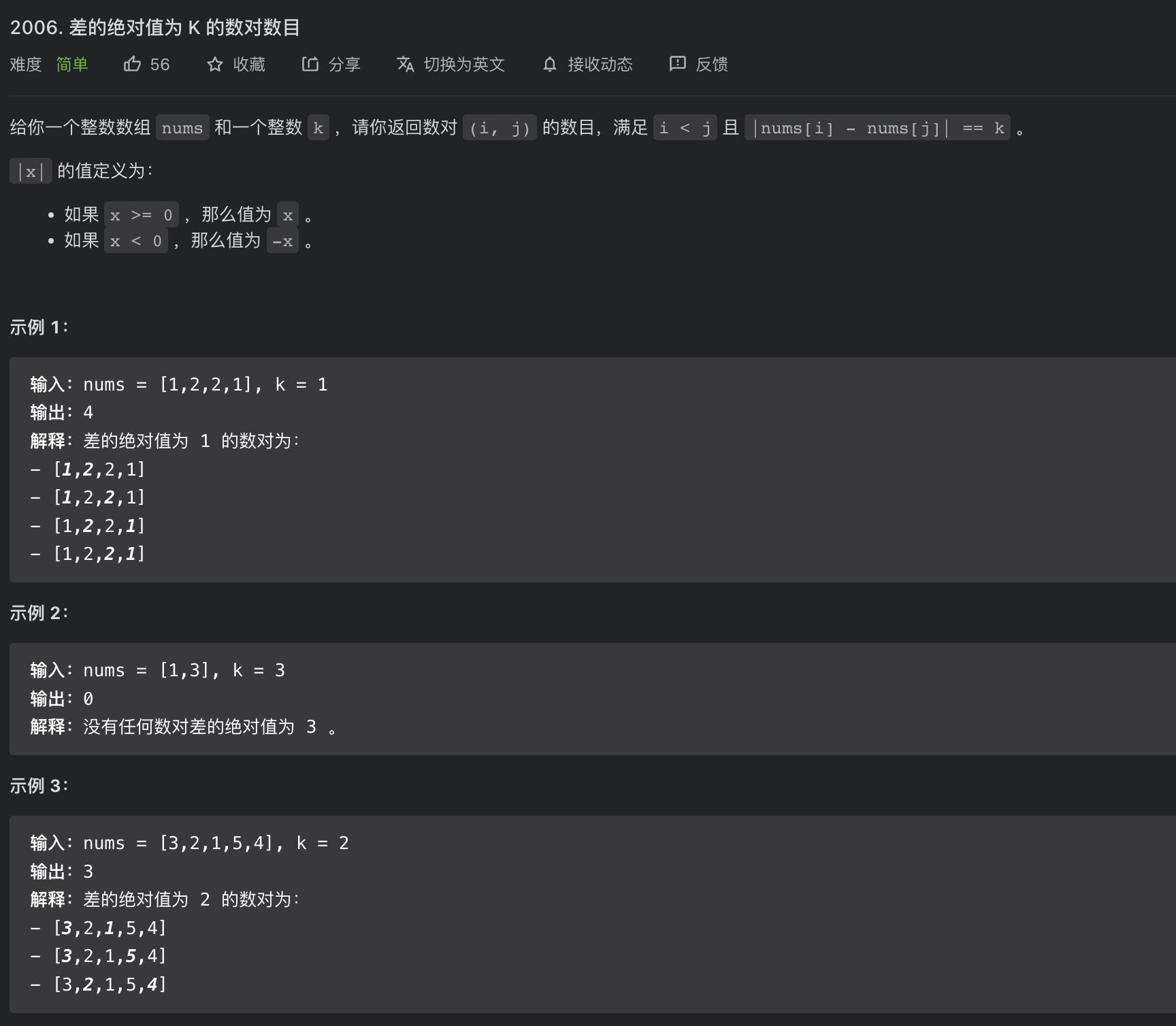

解题思路

对于每个t = nums[j] 而言，是要找与其相对差值为 k 且下标比其小的数（即 t - k 和 t + k），可以采取边遍历边记录某个数出现次数，从而将复杂度优化到 O(n)。

再利用数据范围 1 <= nums[i] <= k，可以直接使用数组充当哈希表。

代码解析（自己）：
1、cnts数组用于保存每个数字在数组中出现次数（代表不同位置的同一数字）
2、t - k >= 1 表示当前遍历到的数字t和差值k 相比t比k大且差值至少是1，比如差值是1，当前遍历数字为2
3、t + k <= 100 表示当前遍历到的数字t和差值k 二者相加小于等于100，意味着当前遍历的数字存在一种可能，那就是它有另一对比他大的数字，在数组最大范围100内
比如

• 数字t为2，差值k为1，那么 2-1 = 1 ，当前遍历的数字2就存在1可以与它结为一对 （1，2）
• 数字t为2，差值k为1，那么 2+1 = 3 <= 100，当前 历的数字2就存在3可以与它结为一对 （2，3）

4、题目要求返回数对 (i, j) 的数目，满足 i < j
这一点代码中ans += cnts[t - k]、ans += cnts[t + k] 就可以做到，因为每次遍历到当前元素的时候，都是取前面遍历过的统计数量，一定能满足i<j

代码

class Solution {
    public int countKDifference(int[] nums, int k) {
        int[] cnts = new int[110];
        int n = nums.length, ans = 0;
        for (int i = 0; i < n; i++) {
            int t = nums[i];
            if (t - k >= 1) ans += cnts[t - k];
            if (t + k <= 100) ans += cnts[t + k];
            cnts[t]++;
        }
        return ans;
    }
}