题目

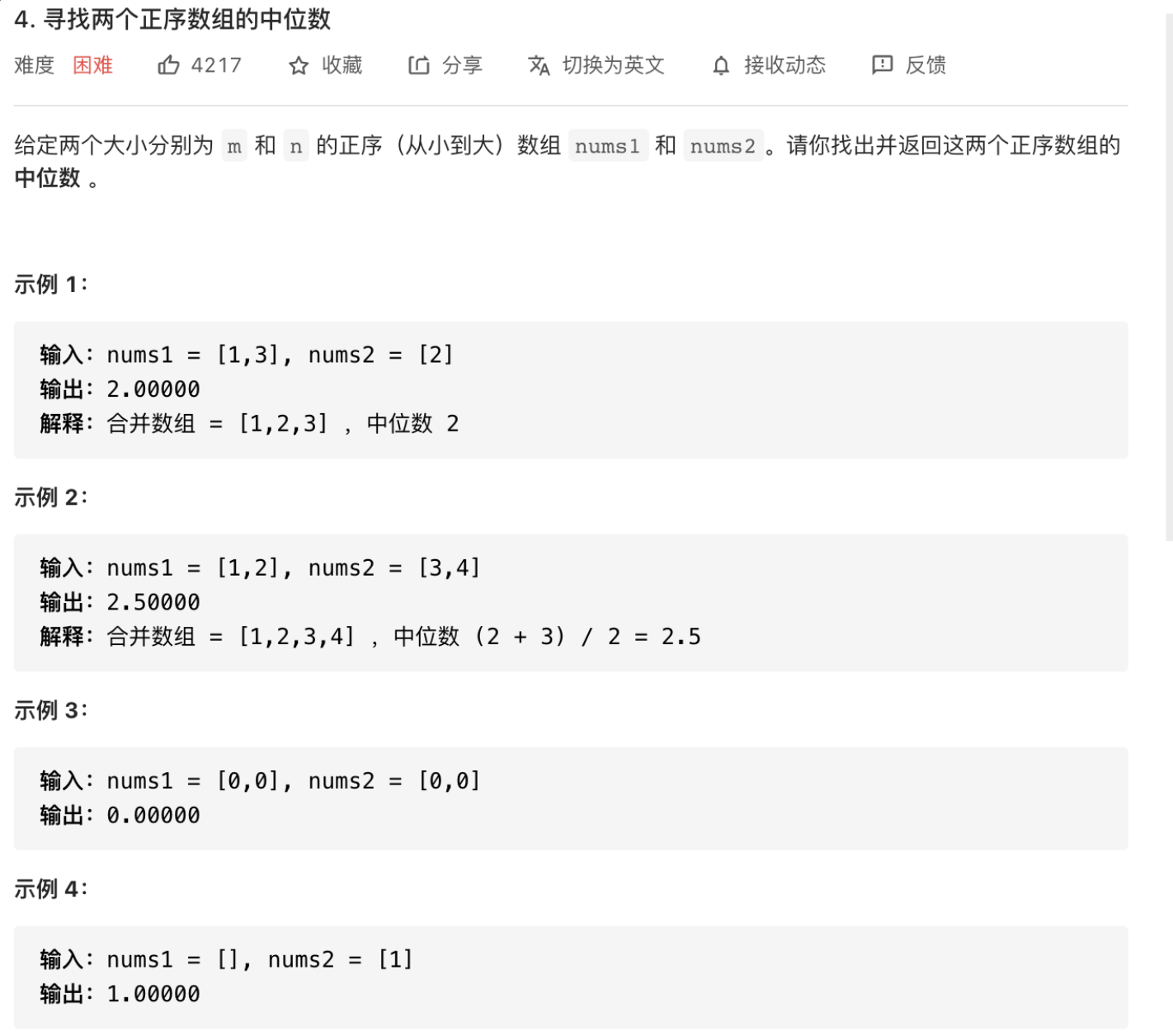
寻找两个有序数组的中位数 - 图1

解题思路

代码来自官方题解。

  • 这一题最容易想到的办法是把两个数组合并，然后取出中位数。但是合并有序数组的操作是 O(m+n) 的，不符合题意。看到题目给的 log的时间复杂度，很容易联想到二分搜索。
  • 关键的问题是如何切分数组 1 和数组 2 。其实就是如何切分数组 1 。先随便二分产生一个 midA，切分的线何时算满足了中位数的条件呢？即，线左边的数都小于右边的数，即，nums1[midA-1] ≤ nums2[midB] && nums2[midB-1] ≤ nums1[midA] 。如果这些条件都不满足，切分线就需要调整。如果 nums1[midA] < nums2[midB-1]，说明 midA 这条线划分出来左边的数小了，切分线应该右移；如果 nums1[midA-1] > nums2[midB]，说明 midA 这条线划分出来左边的数大了，切分线应该左移。经过多次调整以后，切分线总能找到满足条件的解。
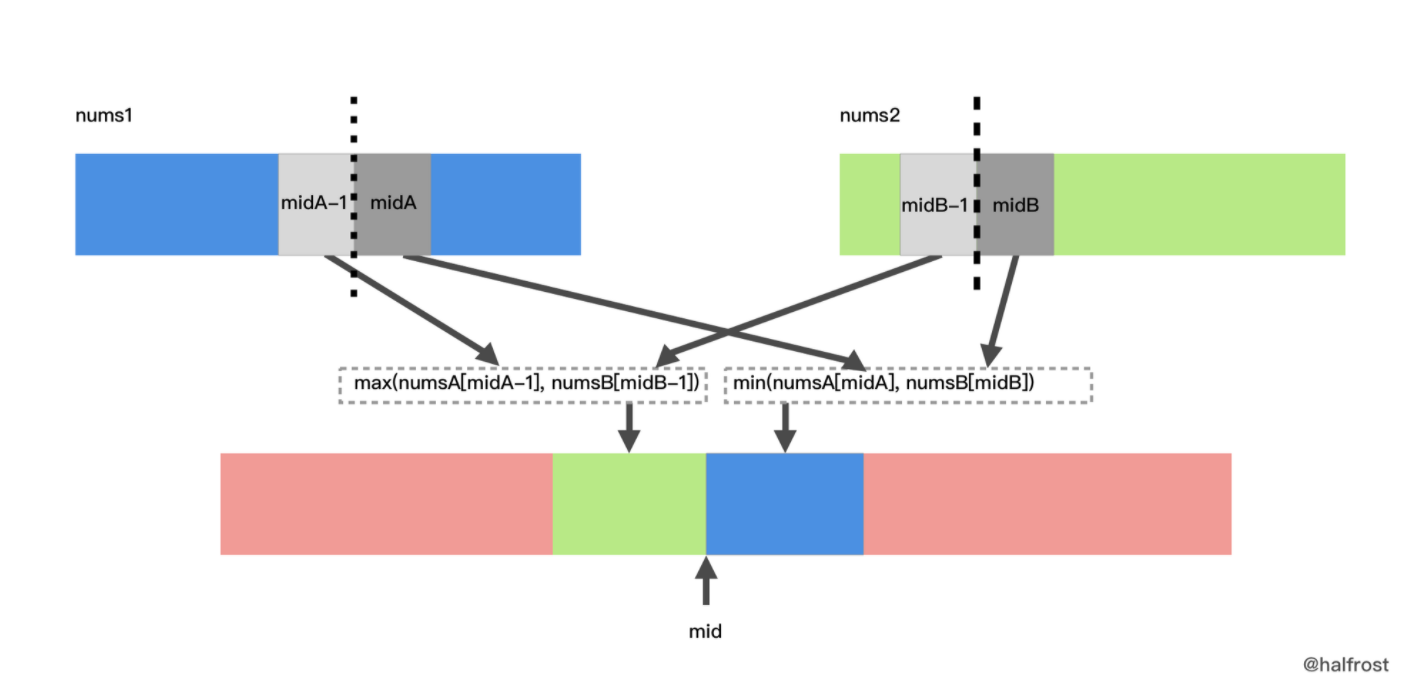
  • 假设现在找到了切分的两条线了，数组 1 在切分线两边的下标分别是 midA - 1 和 midA。数组 2 在切分线两边的下标分别是 midB - 1 和 midB。最终合并成最终数组，如果数组长度是奇数，那么中位数就是 max(nums1[midA-1], nums2[midB-1])。如果数组长度是偶数，那么中间位置的两个数依次是：max(nums1[midA-1], nums2[midB-1]) 和 min(nums1[midA], nums2[midB])，那么中位数就是 (max(nums1[midA-1], nums2[midB-1]) + min(nums1[midA], nums2[midB])) / 2。图示见下图：

寻找两个有序数组的中位数 - 图2

代码

  1. public double findMedianSortedArrays(int[] nums1, int[] nums2) {
  2.       int length1 = nums1.length, length2 = nums2.length;
  3.       int totalLength = length1 + length2;
  4.       if (totalLength % 2 == 1) {
  5.           int midIndex = totalLength / 2;
  6.           double median = getKthElement(nums1, nums2, midIndex + 1);
  7.           return median;
  8.       } else {
  9.           int midIndex1 = totalLength / 2 - 1, midIndex2 = totalLength / 2;
  10.           double median = (getKthElement(nums1, nums2, midIndex1 + 1) + getKthElement(nums1, nums2, midIndex2 + 1)) / 2.0;
  11.           return median;
  12.       }
  13.   }
  15.   public int getKthElement(int[] nums1, int[] nums2, int k) {
  16.       /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
  17.        * 这里的 "/" 表示整除
  18.        * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
  19.        * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
  20.        * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
  21.        * 这样 pivot 本身最大也只能是第 k-1 小的元素
  22.        * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
  23.        * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
  24.        * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
  25.        */
  27.       int length1 = nums1.length, length2 = nums2.length;
  28.       int index1 = 0, index2 = 0;
  29.       int kthElement = 0;
  31.       while (true) {
  32.           // 边界情况
  33.           if (index1 == length1) {
  34.               return nums2[index2 + k - 1];
  35.           }
  36.           if (index2 == length2) {
  37.               return nums1[index1 + k - 1];
  38.           }
  39.           if (k == 1) {
  40.               return Math.min(nums1[index1], nums2[index2]);
  41.           }
  43.           // 正常情况
  44.           int half = k / 2;
  45.           int newIndex1 = Math.min(index1 + half, length1) - 1;
  46.           int newIndex2 = Math.min(index2 + half, length2) - 1;
  47.           int pivot1 = nums1[newIndex1], pivot2 = nums2[newIndex2];
  48.           if (pivot1 <= pivot2) {
  49.               k -= (newIndex1 - index1 + 1);
  50.               index1 = newIndex1 + 1;
  51.           } else {
  52.               k -= (newIndex2 - index2 + 1);
  53.               index2 = newIndex2 + 1;
  54.           }
  55.       }
  56.   }