题目

类型：图

解题思路

题意

• 总共有编号0~7的8个人。
• 每个人都有两种东西，钱和安静值。
• richer数组中的元素[a,b]是用来表示，a比b有钱
• 8个人的安静值数组是quiet，安静值越低代表这个人越安静
• 最后算法返回的结果找出0~7的每个人，比自己富有并且安静值最小的人。比如说编号0这个人，比他富裕且最安静的就是编号5这个人。

算法的思路

这题和图有关，需要用到拓扑排序。

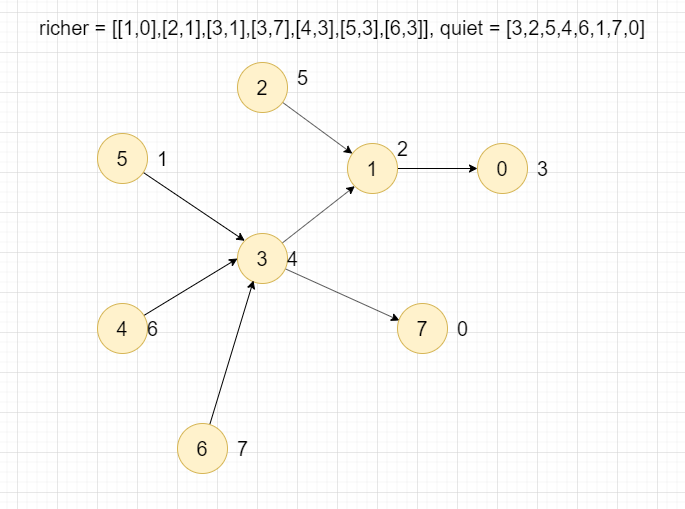
圆圈里面的数字是人物编号，旁边的数字是他的安静值
对于 2、5、4、6节点来说，他们在 answer 中的结果就是他们自己，因为没有人比他们更有钱了，只能选他们自己
而对于 3 来说，比他更有钱的有5、4、6、3（需要包含他自己），在这几个节点中找安静值最小的，也就是 5 号，所以，answer[3] = 5。
对于 1 来说，比他更有钱的有 2、3、1、5、4、6，但是，5、4、6对于结果的贡献值已经传递给 3 了，所以，对于 answer[3]我们在计算 1 的时候是可以直接利用的，也就是说计算 1 的时候并不需要看 5、4、6的值了。
同理，可以得到其他所有节点的 answer 值。

代码

class Solution {
    public int[] loudAndRich(int[][] richer, int[] quiet) {
        // 拓扑排序：取入度为0的先入队，减少它下游节点的入度，如果为0了也入队，直到队列中没有元素为止
        int n = quiet.length;
        // 先整理入度表和邻接表
        int[] inDegree = new int[n];
        boolean[][] g = new boolean[n][n];
        for (int[] r : richer) {
            inDegree[r[1]]++;
            g[r[0]][r[1]] = true;
        }
        // 初始化ans各位为自己
        // 题目说的是：在所有拥有的钱肯定不少于 person x 的人中，person y 是最安静的人
        // 注意这里的不少于，说明可以是自己
        int[] ans = new int[n];
        for (int i = 0; i < n; i++) {
            ans[i] = i;
        }
        // 拓扑排序开始
        int[] queue = new int[n];
        int in = 0, out = 0;
        for (int i = 0; i < n; i++) {
            if (inDegree[i] == 0) {
                queue[in++] = i;
            }
        }
        while (out < in) {
            int p = queue[out++];
            // q是p的下游，也就是p比q有钱
            for (int q = 0; q < g[p].length; q++) {
                if (g[p][q]) {
                    // 如果p的安静值比q小，更新p的安静值对应的那个人
                    // 注意这里p的安静值，并不是原始的quiet数组中的quiet[p]
                    // 而是已经更新后的安静值，所以，应该取quiet[ans[p]]
                    // 这里没有改变原来数组的内容，而是通过ans[p]间接引用的，细细品一下
                    if (quiet[ans[p]] < quiet[ans[q]]) {
                        ans[q] = ans[p];
                    }
                    if (--inDegree[q] == 0) {
                        queue[in++] = q;
                    }
                }
            }
        }
        return ans;
    }
}