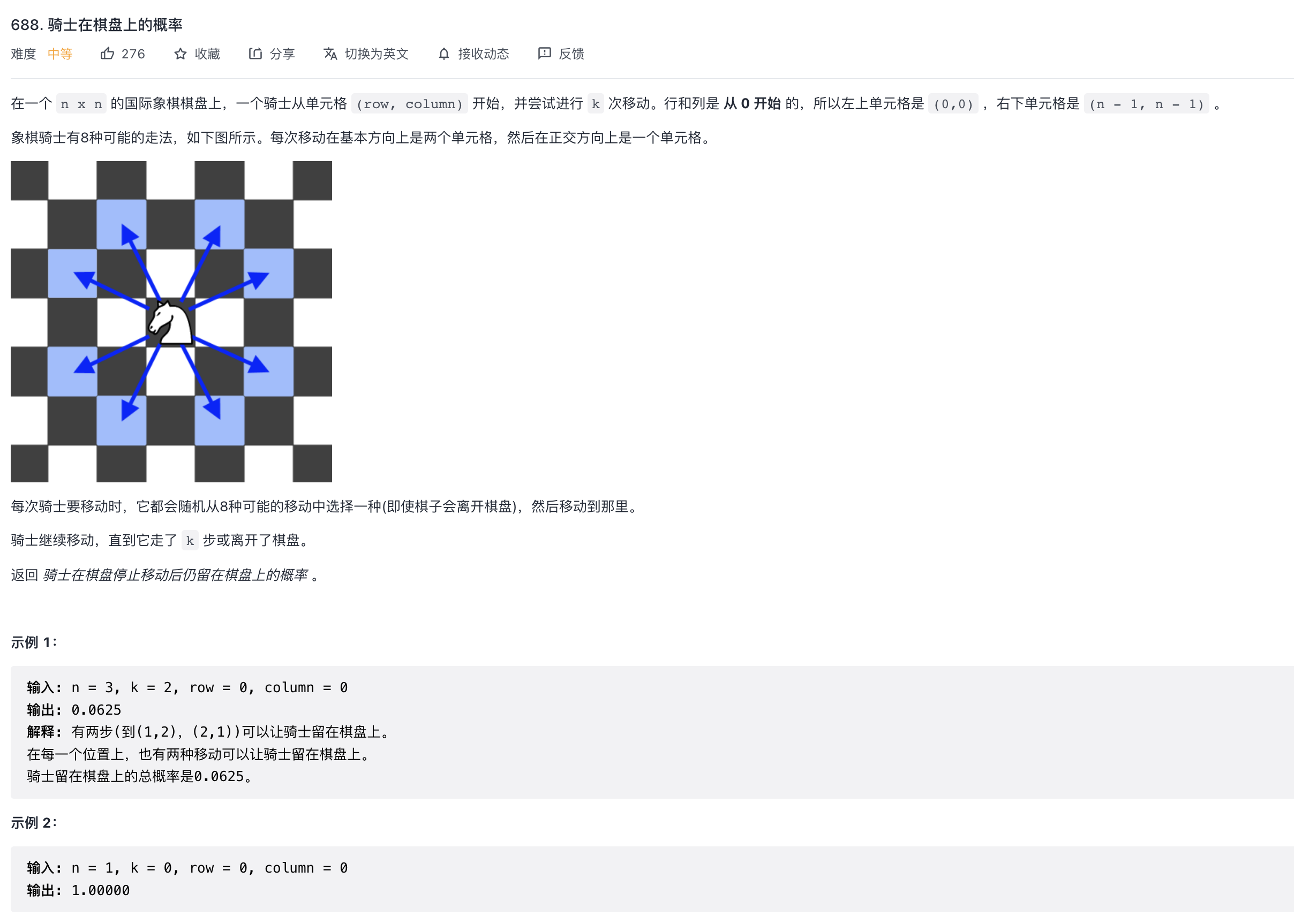
题目

类型：动态规划

image.png

解题思路

线性 DP

定义 f[i][j][p] 为从位置 (i, j) 出发，使用步数不超过 p 步，最后仍在棋盘内的概率。不失一般性考虑 f[i][j][p] 该如何转移，根据题意，移动规则为「八连通」，对下一步的落点 (nx, ny) 进行分情况讨论即可

  • 由于计算的是仍在棋盘内的概率，因此对于 (nx, ny) 在棋盘外的情况，无须考虑；
  • 若下一步的落点 (nx, ny) 在棋盘内，其剩余可用步数为 p - 1 ，则最后仍在棋盘的概率为 f[nx][ny][p - 1] ，则落点 (nx, ny) 对 f[i][j][p] 的贡献为骑士在棋盘上的概率 - 图2 ，其中骑士在棋盘上的概率 - 图3为事件「从 (i, j) 走到 (nx, ny) 」的概率（八连通移动等概率发生），该事件与「到达 (nx, ny) 后进行后续移动并留在棋盘」为相互独立事件。最终的 f[i][j][p] 为「八连通」落点的概率之和，即有骑士在棋盘上的概率 - 图4


代码

  1. class Solution {
  2.     static int[][] dirs = {{-2, -1}, {-2, 1}, {2, -1}, {2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}};
  4.     public double knightProbability(int n, int k, int row, int column) {
  5.         double[][][] dp = new double[k + 1][n][n];
  6.         for (int step = 0; step <= k; step++) {
  7.             for (int i = 0; i < n; i++) {
  8.                 for (int j = 0; j < n; j++) {
  9.                     if (step == 0) {
  10.                         dp[step][i][j] = 1;
  11.                     } else {
  12.                         for (int[] dir : dirs) {
  13.                             int ni = i + dir[0], nj = j + dir[1];
  14.                             if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
  15.                                 dp[step][i][j] += dp[step - 1][ni][nj] / 8;
  16.                             }
  17.                         }
  18.                     }
  19.                 }
  20.             }
  21.         }
  22.         return dp[k][row][column];
  23.     }
  24. }