题目

类型：动态规划

难度：中等

解题思路

1、用f(i, j)来表示从坐标(0,0) 到坐标(i, j)的路径总数，u(i,j)表示坐标(i,j)是否可行，如果坐标(i,j) 有障碍物， u(i,j)=0，否则 u(i, j) = 1。

2、因为 机器人每次只能向下或者向右移动一步，所以从坐标(0,0) 到坐标(i,j) 的路径总数的值只取决于从坐标 (0,0)到坐标(i−1,j)的路径总数和从坐标 (0,0)到坐标(i,j−1)的路径总数，即 f(i,j)只能通过f(i - 1, j)和f(i,j−1)转移得到。当坐标(i,j)本身有障碍的时候，任何路径都到到不了 f(i,j)，此时f(i, j) = 0

3、如果坐标 (i−1,j)没有障碍，那么就意味着从坐标(i−1,j)可以走到(i, j) ，即 (i−1,j)位置对f(i,j)的贡献为f(i−1,j)，同理，当坐标(i,j−1)没有障碍的时候，(i,j−1)位置对 f(i,j) 的贡献为f(i,j−1)。

综上所述，我们可以得到这样的动态规划转移方程：

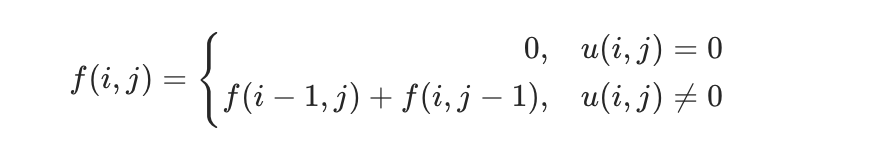
代码

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int n = obstacleGrid.length, m = obstacleGrid[0].length;
        int[] f = new int[m];
        f[0] = obstacleGrid[0][0] == 0 ? 1 : 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (obstacleGrid[i][j] == 1) {
                    f[j] = 0;
                    continue;
                }
                if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {
                    f[j] += f[j - 1];
                }
            }
        }
        return f[m - 1];
    }
}