题目

类型：动态规划

解题思路

这道题目其实是最长递增子序列的一个变种，因为每次合法的嵌套是大的套小的，相当于在二维平面中找一个最长递增的子序列，其长度就是最多能嵌套的信封个数。
前面说的标准 LIS 算法只能在一维数组中寻找最长子序列，而我们的信封是由 (w, h) 这样的二维数对形式表示的，如何把 LIS 算法运用过来呢？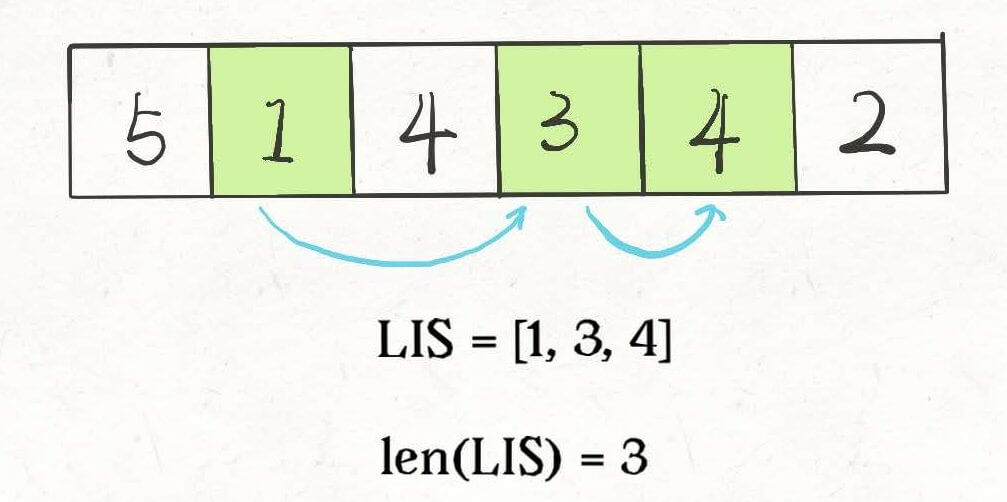

读者也许会想，通过 w × h 计算面积，然后对面积进行标准的 LIS 算法。但是稍加思考就会发现这样不行，比如 1 × 10 大于 3 × 3，但是显然这样的两个信封是无法互相嵌套的。
这道题的解法比较巧妙：
先对宽度 w 进行升序排序，如果遇到 w 相同的情况，则按照高度 h 降序排序；之后把所有的 h 作为一个数组，在这个数组上计算 LIS 的长度就是答案。
画个图理解一下，先对这些数对进行排序：

然后在 h 上寻找最长递增子序列，这个子序列就是最优的嵌套方案：

为什么呢？稍微思考一下就明白了：
首先，对宽度 w 从小到大排序，确保了 w 这个维度可以互相嵌套，所以我们只需要专注高度 h 这个维度能够互相嵌套即可。
其次，两个 w 相同的信封不能相互包含，所以对于宽度 w 相同的信封，对高度 h 进行降序排序，保证 LIS 中不存在多个 w 相同的信封（因为题目说了长宽相同也无法嵌套）。

代码

public class RussianDollEnvelopes {
    /**
     * envelopes = [[w, h], [w, h]...]
     */
    public int maxEnvelopes(int[][] envelopes) {
        int n = envelopes.length;
        // 按宽度升序排列，如果宽度一样，则按高度降序排列
        Arrays.sort(envelopes, new Comparator<int[]>() {
            @Override
            public int compare(int[] a, int[] b) {
                return a[0] == b[0] ?
                        b[1] - a[1] : a[0] - b[0];
            }
        });
        // 对高度数组寻找 LIS
        int[] height = new int[n];
        for (int i = 0; i < n; i++) {
            height[i] = envelopes[i][1];
        }
        return lengthOfLIS(height);
    }
    int lengthOfLIS(int[] nums) {
        int len = nums.length;
        if (len <= 1) {
            return len;
        }
        // tail 数组的定义：长度为 i + 1 的上升子序列的末尾最小是几
        int[] tail = new int[len];
        // 遍历第 1 个数，直接放在有序数组 tail 的开头
        tail[0] = nums[0];
        // end 表示有序数组 tail 的最后一个已经赋值元素的索引
        int end = 0;
        for (int i = 1; i < len; i++) {
            int left = 0;
            // 这里，因为当前遍历的数，有可能比有序数组 tail 数组实际有效的末尾的那个元素还大
            // 【逻辑 1】因此 end + 1 应该落在候选区间里
            int right = end + 1;
            while (left < right) {
                // 选左中位数不是偶然，而是有原因的，原因请见 LeetCode 第 35 题题解
                // int mid = left + (right - left) / 2;
                int mid = (left + right) >>> 1;
                if (tail[mid] < nums[i]) {
                    // 中位数肯定不是要找的数，把它写在分支的前面
                    left = mid + 1;
                } else {
                    right = mid;
                }
            }
            // 因为 【逻辑 1】，因此一定能找到第 1 个大于等于 nums[i] 的元素
            // 因此，无需再单独判断，直接更新即可
            tail[left] = nums[i];
            // 但是 end 的值，需要更新，当前仅当更新位置在当前 end 的下一位
            if (left == end + 1) {
                end++;
            }
        }
        // 此时 end 是有序数组 tail 最后一个元素的索引
        // 题目要求返回的是长度，因此 +1 后返回
        end++;
        return end;
    }
}