题目

类型：数学

解题思路

为了将支付的金额最小化，除了需要将每次支付的金额控制在较低值以外，还需要在猜数字的过程中缩小所选数字的范围。
当猜了数字 x 并且猜错时，会知道 x 比所选数字大还是小。
如果 x 比所选数字大，则任何比 x 大的数字一定都比所选数字大，因此应该在比 x 小的数字中继续猜数字。
如果 x 比所选数字小，同理可知应该在比 x 大的数字中继续猜数字。

用 f(i,j) 表示在范围 [i, j] 内确保胜利的最少金额，目标是计算 f(1, n)。
假设第一次猜的数字是 x 并且猜错，则需要支付金额 x，当 x 大于所选数字时，为了确保胜利还需要支付的金额是 f(1,x−1)，当 x 小于所选数字时，为了确保胜利还需要支付的金额是 f(x + 1, n)。为了在任何情况下都能确保胜利，应考虑最坏情况，计算 f(1, n) 时应取上述两者的最大值：
f(1,n)=x+max(f(1,x−1),f(x+1,n))。
为了将确保胜利的金额最小化，需要遍历从 1 到 n 的所有可能的 x，使得 f(1, n) 的值最小：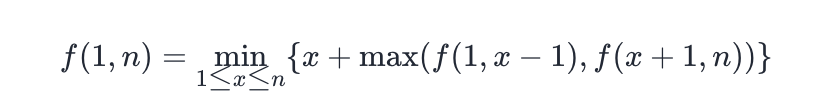

由于 f(1, x - 1) 和 f(x + 1, n) 都是比原始问题 f(1, n) 规模更小的问题，因此可以使用动态规划的方法求解。
动态规划的状态为 f(i, j)，表示在范围 [i, j] 内确保胜利的最少金额。

当 i = j 时范围 [i, j] 只包含 1 个数字，所选数字一定是范围内的唯一的数字，不存在猜错的情况，因此 f(i, j) = 0；当 i > j 时范围 [i, j] 不存在，因此 f(i, j) = 0。
综合上述两种情况可知，动态规划的边界情况是：当 i≥j 时，f(i,j)=0。

当 i<j 时，在范围 [i, j] 内第一次猜的数字可能是该范围内的任何一个数字。在第一次猜的数字是 k 的情况下（i≤k≤j），在范围 [i,j] 内确保胜利的最少金额是 k+max(f(i,k−1),f(k+1,j))。需要遍历全部可能的 k 找到在范围 [i, j] 内确保胜利的最少金额，因此状态转移方程如下：

由于状态转移方程为根据规模小的子问题计算规模大的子问题，因此计算子问题的顺序为先计算规模小的子问题，后计算规模大的子问题，需要注意循环遍历的方向。

代码

class Solution {
    public int getMoneyAmount(int n) {
        int[][] f = new int[n + 1][n + 1];
        for (int i = n - 1; i >= 1; i--) {
            for (int j = i + 1; j <= n; j++) {
                int minCost = Integer.MAX_VALUE;
                for (int k = i; k < j; k++) {
                    int cost = k + Math.max(f[i][k - 1], f[k + 1][j]);
                    minCost = Math.min(minCost, cost);
                }
                f[i][j] = minCost;
            }
        }
        return f[1][n];
    }
}