题目

类型：双指针

解题思路

从三个不发送好友请求的条件来看，以 y 的角度来说，可总结为：

• 年龄比我小的不考虑（同龄的可以）
• 年龄比我大可以考虑，但是不能超过一定范围则不考虑。

对于一个确定的 y 而言，会发送好友请求的 x 范围为连续段：

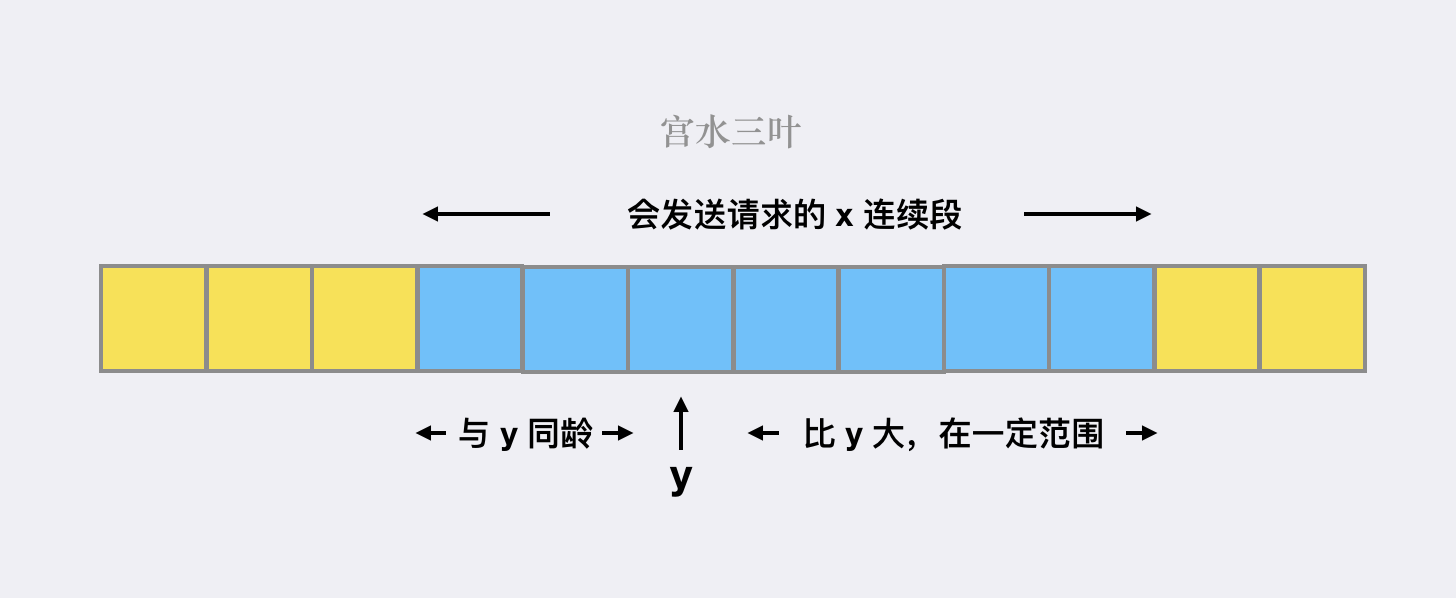
随着 y 的逐渐增大，对应的 x 连续段的左右边界均逐渐增大（数轴上均往右移动）。

因此，可以先对 ages 进行排序，枚举每个 y = ages[k] ，同时使用 i 和 j 维护左右区间，[i, j) 代表在 ages 上会往 y = ages[k] 发送请求的 x 连续段，统计每个 y = ages[k] 的 x 有多少个即是答案，同时需要注意在 [i, j) 范围内是包含 y = ages[k] 自身，统计区间长度时需要进行 -1 操作。

代码

class Solution {
    int N = 130;
    public int numFriendRequests(int[] ages) {
        int[] nums = new int[N];
        for (int i : ages) nums[i]++;
        for (int i = 1; i < N; i++) nums[i] += nums[i - 1];
        int ans = 0;
        for (int y = 1, x = 1; y < N; y++) {
            int a = nums[y] - nums[y - 1]; // 有 a 个 y
            if (a == 0) continue;
            if (x < y) x = y;
            while (x < N && check(x, y)) x++;
            int b = nums[x - 1] - nums[y - 1] - 1; // [y, x) 为合法的 x 范围，对于每个 y 而言，有 b 个 x
            if (b > 0) ans += b * a;
        }
        return ans;
    }
    boolean check(int x, int y) {
        if (y <= 0.5 * x + 7) return false;
        if (y > x) return false;
        if (y > 100 && x < 100) return false; 
        return true;
    }
}