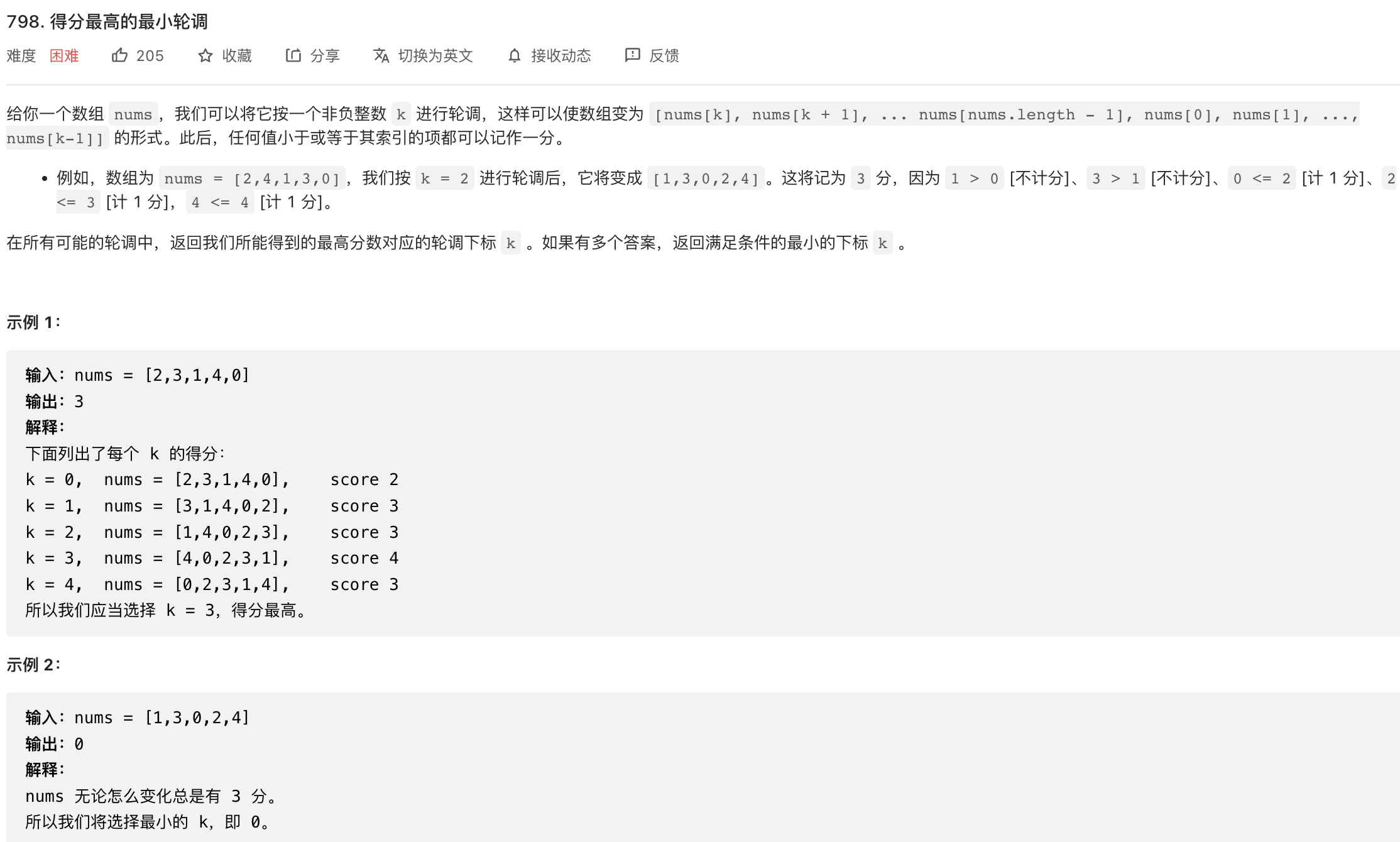
题目

类型：数组

解题思路

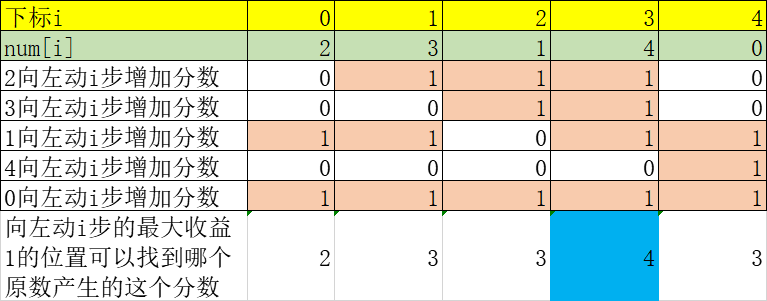
解释一下：如2向左动i步增加分数,
2向左0步，没动，2>0，0分。
2向左1步到了4位置，4>2，1分。
2向左2步到了3位置，3>2，1分。
2向左3步到了2位置，2=2，1分。
2向左4步到了1位置，1<2，0分。
类似的看一眼后面几行。

对于某一个i列求和，是整体向左移动的步数能产生的分数。比如i==0，没动，数字1和0产生分数了。
类似的看一眼后面几列。
因此：
我们想知道哪一个列的累加和最大，而且出现的早。
我们当然可以暴力的n*n搞一个二维的表，最先出现的列累加和最大的就是答案，比如例子里面的i==3时。但是这样会超时。
对于很长的一个连续的一段计数1的区间，我们要不要给每一个位置都赋值1次呢？
不需要。
差分可以让我们只管连续1的首尾，不必给每一个位置都赋值1。只要从开始位置+1,结尾的下一个位置-1,遍历过程，中间自然计数，像极了前缀和吧？只不过他要有个结尾减去这个计数影响。
即差分==从哪开始计数，到哪里计数结束，中间计数位置不用一个个赋值

代码

class Solution {
    public int bestRotation(int[] nums) {
        int n = nums.length;
        int[] help = new int[n];
        int cur = 0;
        help[cur] += 1;
        for (int i = 0; i < n; i++) {
            if ((cur = nums[i]) != 0) {
                int one = n - cur;
                help[(i + 1) % n] += 1;
                help[(i + 1 + one) % n] -= 1;
            }
        }
        int ans = 0;
        int max = 0, sum = 0;
        for (int i = 0; i < n; i++) {
            sum += help[i];
            if (sum > max) {
                max = sum;
                ans = i;
            }
        }
        return ans;
    }
}