题目

类型：动态规划
image.png

解题思路

用动态规划

设 f[i][j] 表示使用数字 1,2,⋯,i 的排列构成长度为 i 的数组，并且恰好包含 j 个逆序对的方案数。在进行状态转移时，可以考虑第 i 个元素选取了 1,2,⋯,i 中的哪个数字。
假设选取了数字 k，那么数组的前 i−1 个元素由 1,⋯,k−1 以及 k+1,⋯,i 的某个排列构成。数组中的逆序对的个数可以看成如下的两部分之和：

  • 数字 k 与前 i−1 个元素产生的逆序对的个数；
  • 前 i−1 个元素「内部」产生的逆序对个数。

对于第一部分而言，可以求出：数字 k 会贡献 i−k 个逆序对，即 k+1,⋯,i 与 k 分别产生一个逆序对。
对于第二部分而言，希望它能够有 j−(i−k) 个逆序对，这样才能一共有 j 个逆序对。由于关心的是前 i−1 个元素「内部」产生的逆序对个数，而逆序对只和元素的「相对大小」有关，因此可以：

  • 1,⋯,k−1 这些元素保持不变；
  • k+1,⋯,i 这些元素均减少 1，变成 k,⋯,i−1。

使得前 i−1 个元素中，任意两个元素的相对大小都不发生变化。此时，我们的目标变成了「对于 1,2,⋯,i−1，希望它能够有 j−(i−k) 个逆序对」，这就是动态规划中的子任务 f[i−1][j−(i−k)]。

因此，就可以通过枚举 k 得到状态转移方程：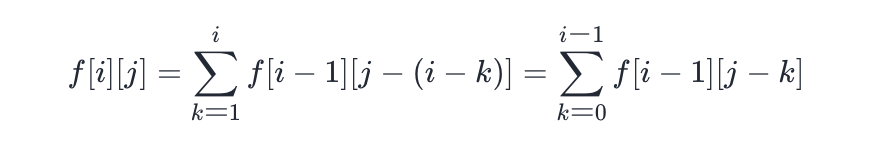
image.png
边界条件为：

  • f[0][0] = 1，即不用任何数字可以构成一个空数组，它包含 0 个逆序对；
  • f[i][j < 0] = 0，由于逆序对的数量一定是非负整数，因此所有 j<0 的状态的值都为 0。不需要显式地存储这些状态，只需要在进行状态转移遇到这样的项时，注意特殊判断即可。

最终的答案即为 f[n][k]。

代码

  1. class Solution {
  2.     public int kInversePairs(int n, int k) {
  3.         final int MOD = 1000000007;
  4.         int[][] f = new int[2][k + 1];
  5.         f[0][0] = 1;
  6.         for (int i = 1; i <= n; ++i) {
  7.             for (int j = 0; j <= k; ++j) {
  8.                 int cur = i & 1, prev = cur ^ 1;
  9.                 f[cur][j] = (j - 1 >= 0 ? f[cur][j - 1] : 0) - (j - i >= 0 ? f[prev][j - i] : 0) + f[prev][j];
  10.                 if (f[cur][j] >= MOD) {
  11.                     f[cur][j] -= MOD;
  12.                 } else if (f[cur][j] < 0) {
  13.                     f[cur][j] += MOD;
  14.                 }
  15.             }
  16.         }
  17.         return f[n & 1][k];
  18.     }
  19. }