题目

类型：回溯

难度：中等

解题思路

使用递归 + 回溯

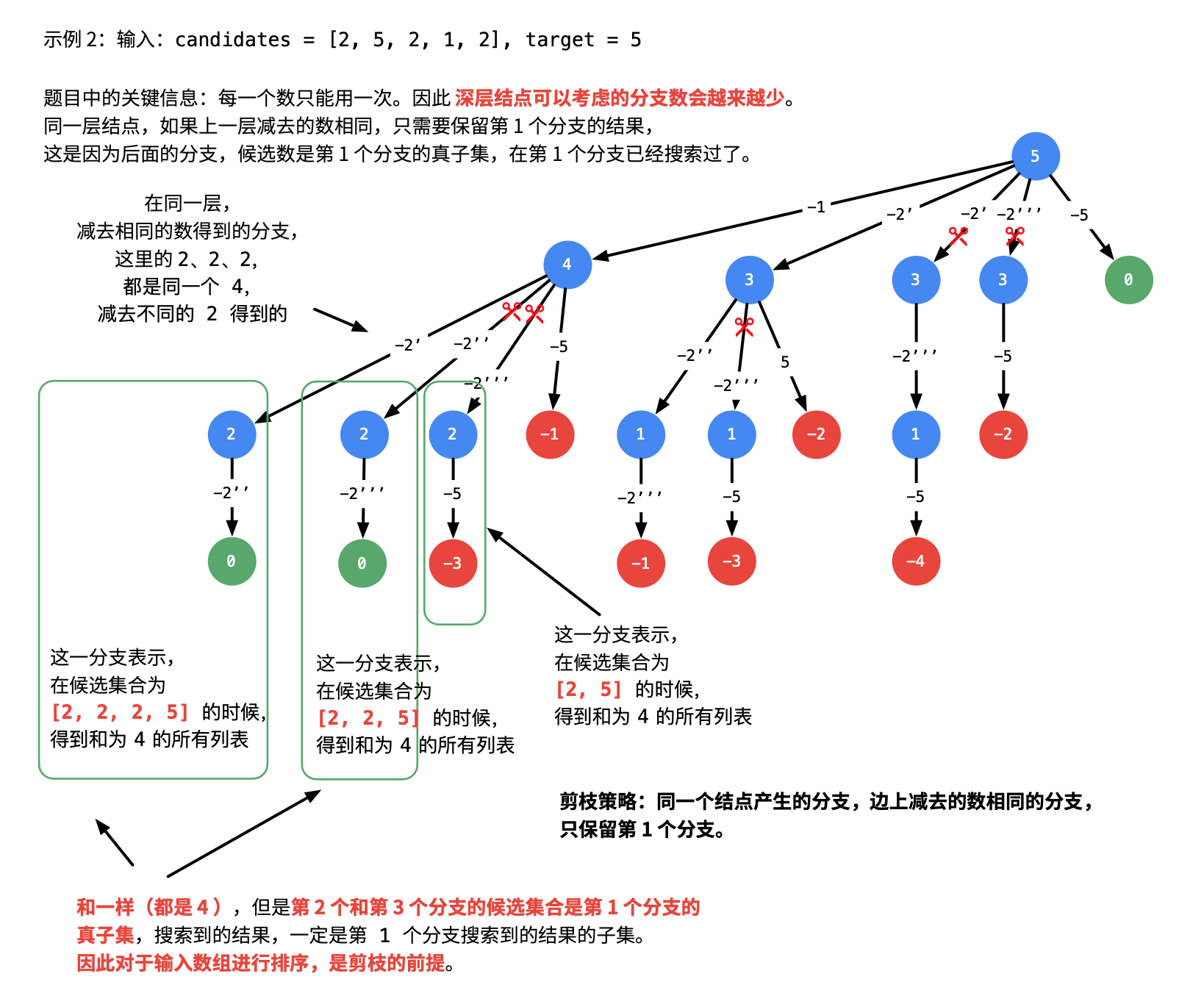
与第 39 题（组合之和）的差别在于这题每个数字在每个组合中只能使用一次，相同点是相同数字列表的不同排列视为一个结果。

由上述分析可以得出，如何去重是重点

两种方法，一种是使用哈希表，这种方法比较复杂。第二种方法就用和39题一样的思路，我们先排序，在搜索的过程中检测分支是不是有重复结果。

代码

package backtracking;
import java.util.*;
public class CombinationSumII {
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        int len = candidates.length;
        List<List<Integer>> res = new ArrayList<>();
        if (len == 0) {
            return res;
        }
        // 关键步骤
        Arrays.sort(candidates);
        Deque<Integer> path = new ArrayDeque<>(len);
        dfs(candidates, len, 0, target, path, res);
        return res;
    }
    /**
     * @param candidates 候选数组
     * @param len        冗余变量
     * @param begin      从候选数组的 begin 位置开始搜索
     * @param target     表示剩余，这个值一开始等于 target，基于题目中说明的"所有数字（包括目标数）都是正整数"这个条件
     * @param path       从根结点到叶子结点的路径
     * @param res
     */
    private void dfs(int[] candidates, int len, int begin, int target, Deque<Integer> path, List<List<Integer>> res) {
        if (target == 0) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = begin; i < len; i++) {
            // 大剪枝：减去 candidates[i] 小于 0，减去后面的 candidates[i + 1]、candidates[i + 2] 肯定也小于 0，因此用 break
            if (target - candidates[i] < 0) {
                break;
            }
            // 小剪枝：同一层相同数值的结点，从第 2 个开始，候选数更少，结果一定发生重复，因此跳过，用 continue
            if (i > begin && candidates[i] == candidates[i - 1]) {
                continue;
            }
            path.addLast(candidates[i]);
            // 调试语句 ①
            // System.out.println("递归之前 => " + path + "，剩余 = " + (target - candidates[i]));
            // 因为元素不可以重复使用，这里递归传递下去的是 i + 1 而不是 i
            dfs(candidates, len, i + 1, target - candidates[i], path, res);
            path.removeLast();
            // 调试语句 ②
            // System.out.println("递归之后 => " + path + "，剩余 = " + (target - candidates[i]));
        }
    }
}