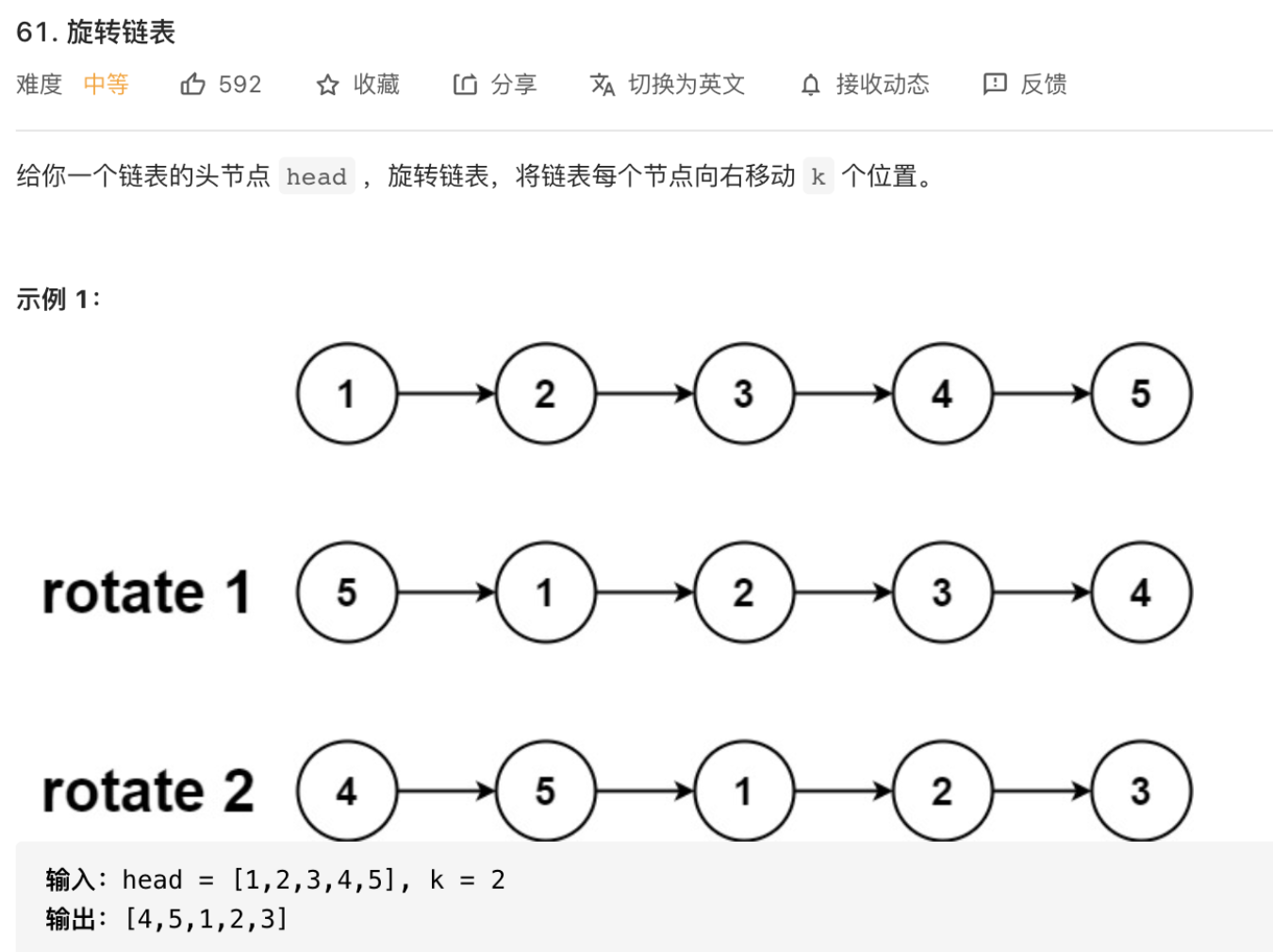
题目

解题思路

记给定链表的长度为 n，当向右移动的次数 k≥n 时，我们仅需要向右移动 k mod n 次即可。因为每 n 次移动都会让链表变为原状。

这样我们可以知道，新链表的最后一个节点为原链表的第 (n−1)−(k mod n) 个节点（从 0 开始计数）。

这样，我们可以先将给定的链表连接成环，然后将指定位置断开。

具体代码中，我们首先计算出链表的长度 n，并找到该链表的末尾节点，将其与头节点相连。这样就得到了闭合为环的链表。然后我们找到新链表的最后一个节点（即原链表的第 (n−1)−(k mod n) 个节点），将当前闭合为环的链表断开，即可得到我们所需要的结果。

特别地，当链表长度不大于 1，或者 k 为 n 的倍数时，新链表将与原链表相同，无需进行任何处理。

代码

class Solution {
    public ListNode rotateRight(ListNode head, int k) {
        if (k == 0 || head == null || head.next == null) {
            return head;
        }
        int n = 1;
        ListNode iter = head;
        while (iter.next != null) {
            iter = iter.next;
            n++;
        }
        int add = n - k % n;
        if (add == n) {
            return head;
        }
        iter.next = head;
        while (add-- > 0) {
            iter = iter.next;
        }
        ListNode ret = iter.next;
        iter.next = null;
        return ret;
    }
}