题目

类型：树

解题思路

题目所说的四分树，其实就是用来表示矩阵数据的一种数据结构。

把一个边长为 2 的幂的正方形均分成 4 块，然后再均分到不能均分为止即为叶子节点。

树的节点分成两种：一种是叶子节点（矩阵内所有的取值一样），一种不是叶子节点（矩阵内的取值不一样，需要继续细分）。

建立四叉树的过程：

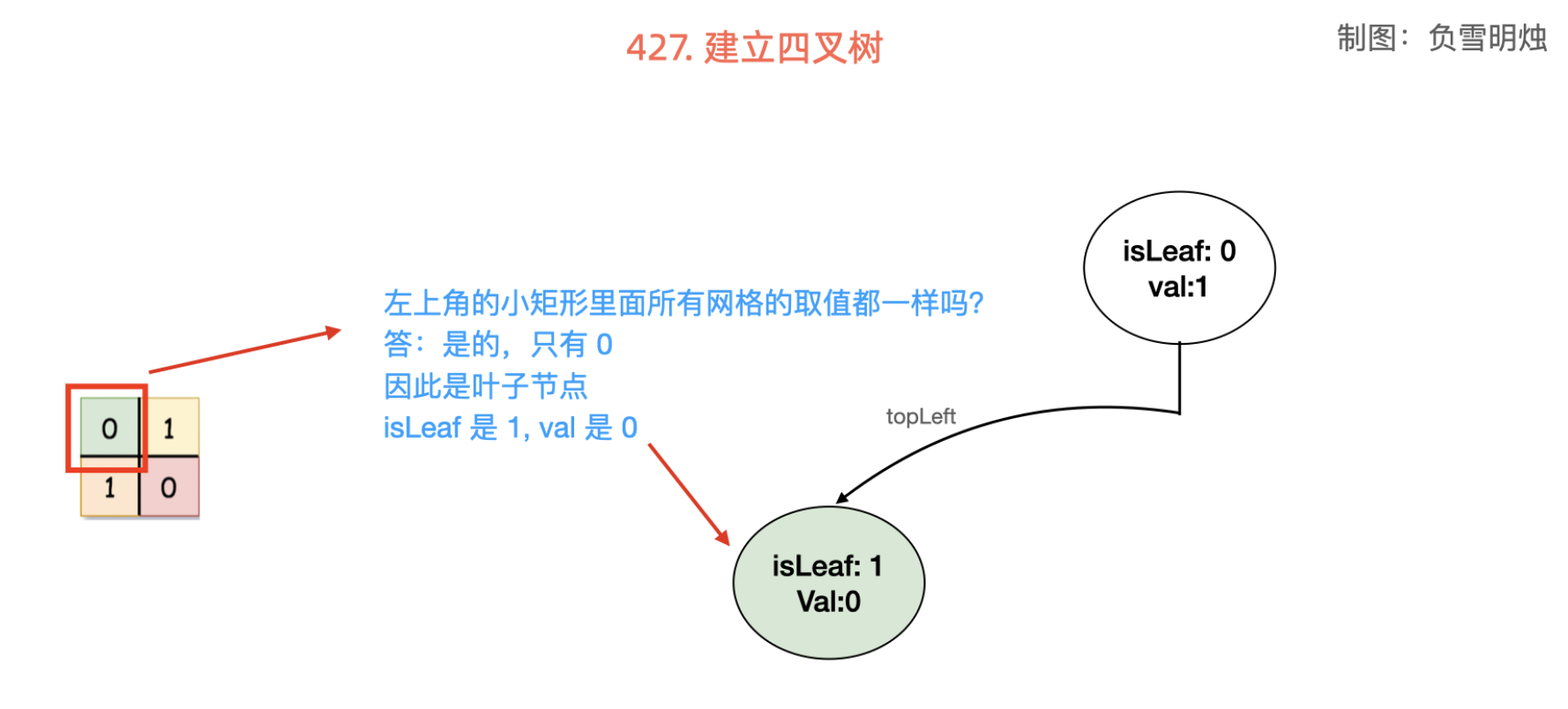
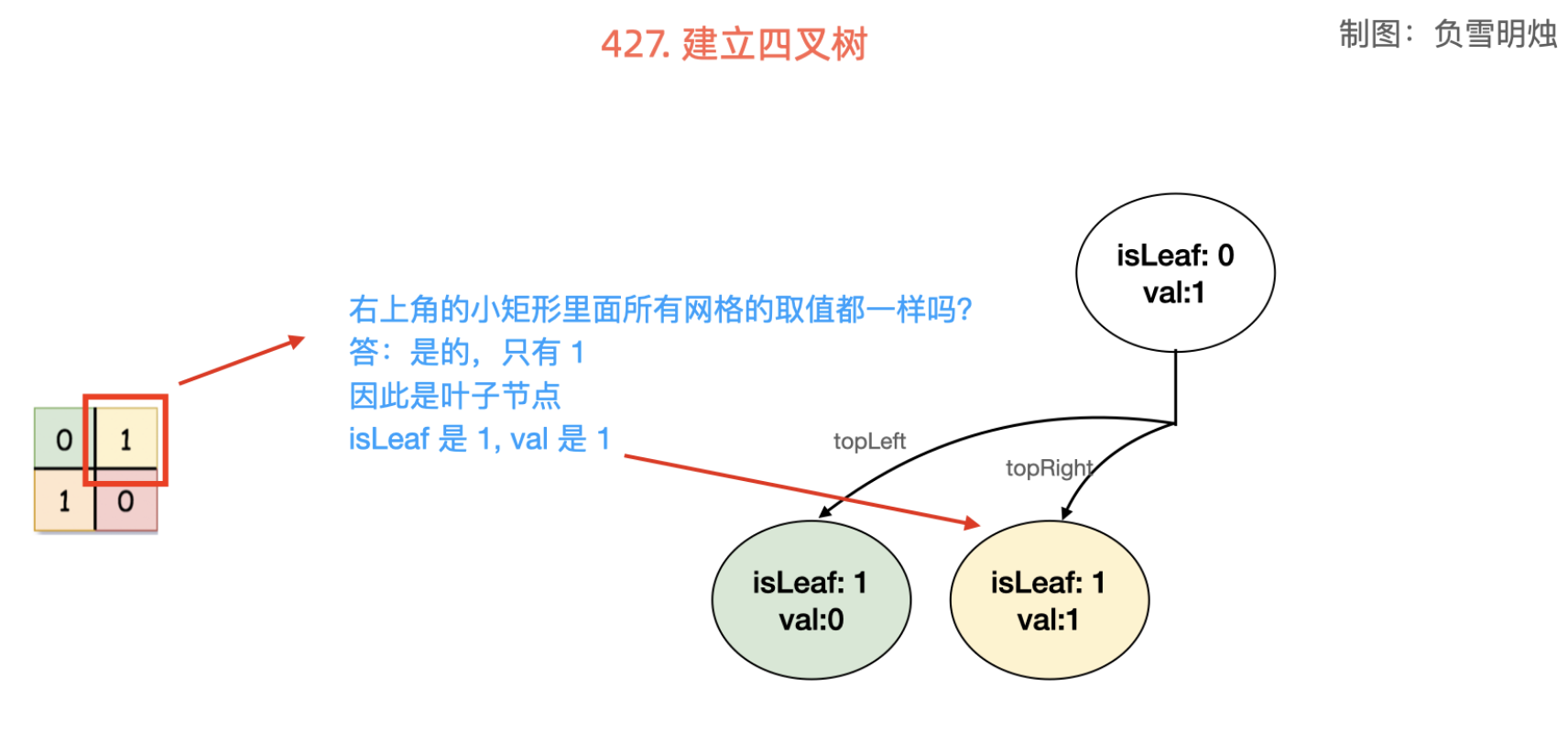
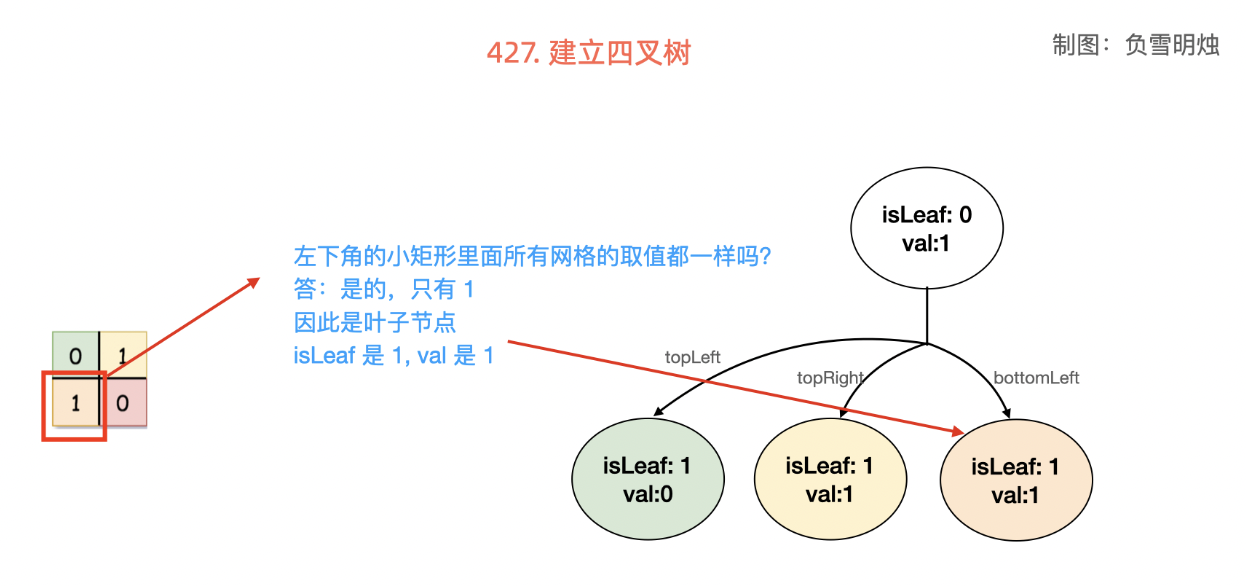
使用前缀和优化「判断全 0 和全 1」的操作：对矩阵 grid 求前缀和数组 sum，对于一个「以左上角为 (a, b)(a,b)，右下角为 (c, d)(c,d) 」的子矩阵而言，其所包含的格子总数为 tot = (c - a + 1) * (d - b + 1) 个，当且仅当矩阵和为 0 或 tot 时，矩阵全 0 或 1。

代码

class Solution {
    static int[][] sum = new int[70][70];   
    int[][] g;
    public Node construct(int[][] grid) {
        g = grid;
        int n = grid.length;
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + g[i - 1][j - 1];
            }
        }
        return dfs(0, 0, n - 1, n - 1);
    }
    Node dfs(int a, int b, int c, int d) {
        int cur = sum[c + 1][d + 1] - sum[a][d + 1] - sum[c + 1][b] + sum[a][b];
        int dx = c - a + 1, dy = d - b + 1, tot = dx * dy;
        if (cur == 0 || cur == tot) return new Node(g[a][b] == 1, true);
        Node root = new Node(g[a][b] == 1, false);
        root.topLeft = dfs(a, b, a + dx / 2 - 1, b + dy / 2 - 1);
        root.topRight = dfs(a, b + dy / 2, a + dx / 2 - 1, d);
        root.bottomLeft = dfs(a + dx / 2, b, c, b + dy / 2 - 1);
        root.bottomRight = dfs(a + dx / 2, b + dy / 2, c, d);
        return root;
    }
}