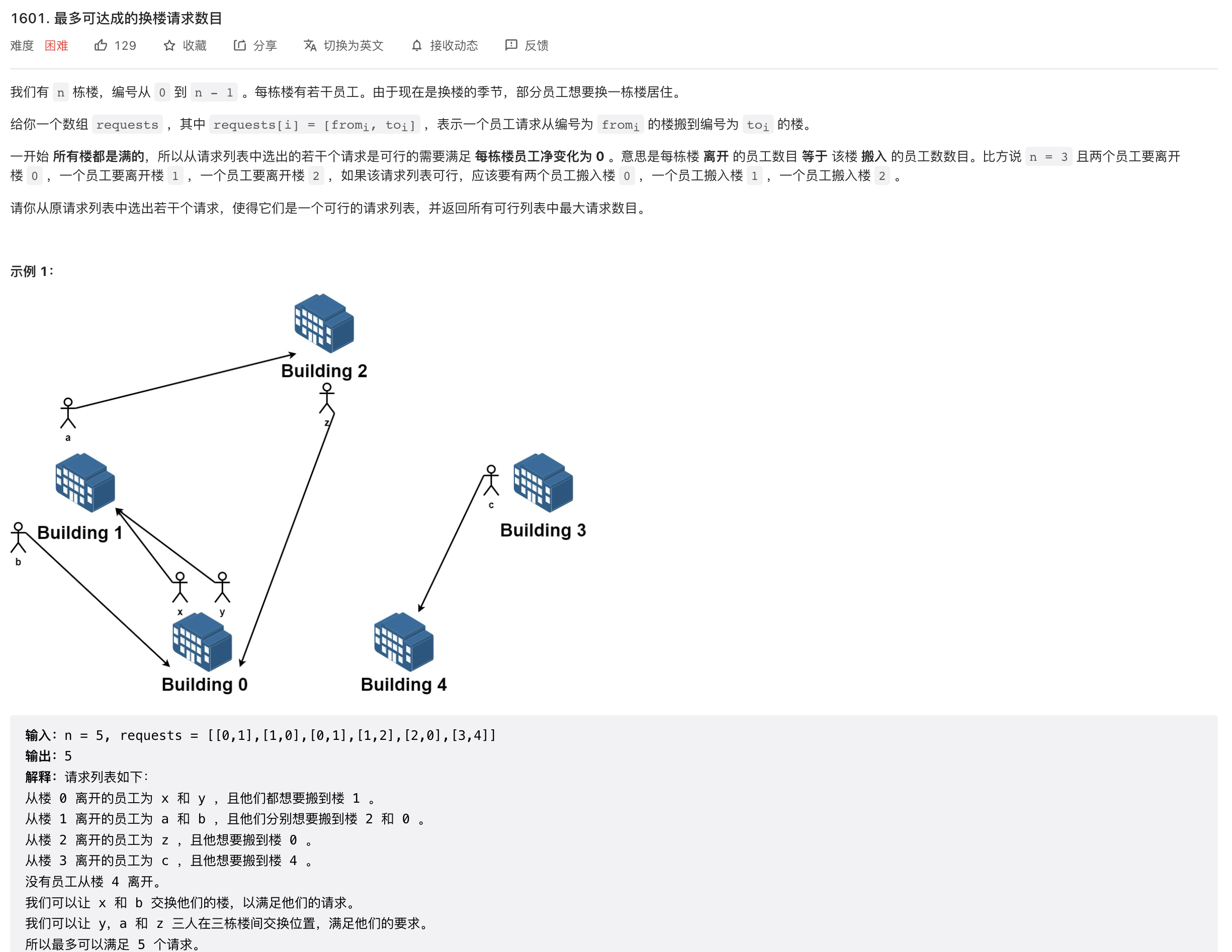
题目

类型：位运算

解题思路

requests 的长度为 m 。n 的范围为 20 ，而 m 的范围为 16。

根据每个 requests[i] 是否选择，共有 种状态（不超过 70000 种状态）。
可以采用「二进制枚举」的思路来求解，使用二进制数 state 来表示对 requests[i] 的选择情况，当 state 的第 k 位为 1 ，代表 requests[k] 被选择。
枚举所有的 state 并进行合法性检查，从中选择出包含请求数的最多（二进制表示中包含 11 个数最多）的合法 state ，其包含的请求数量即是答案。
其中统计 state 中 1 的个数可以使用 lowbit，复杂度为 O(m)，判断合法性则直接模拟即可（统计每座建筑的进出数量，最后判定进出数不相等的建筑数量是为 0），复杂度为 O(m)，整体计算量为不超过 ，可以过。

代码

class Solution {
    int[][] rs;
    public int maximumRequests(int n, int[][] requests) {
        rs = requests;
        int m = rs.length, ans = 0;
        for (int i = 0; i < (1 << m); i++) {
            int cnt = getCnt(i);
            if (cnt <= ans) continue;
            if (check(i)) ans = cnt;
        }
        return ans;
    }
    boolean check(int s) {
        int[] cnt = new int[20];
        int sum = 0;
        for (int i = 0; i < 16; i++) {
            if (((s >> i) & 1) == 1) {
                int a = rs[i][0], b = rs[i][1];
                if (++cnt[a] == 1) sum++;
                if (--cnt[b] == 0) sum--;
            }
        }
        return sum == 0;
    }
    int getCnt(int s) {
        int ans = 0;
        for (int i = s; i > 0; i -= (i & -i)) ans++;
        return ans;
    }
}