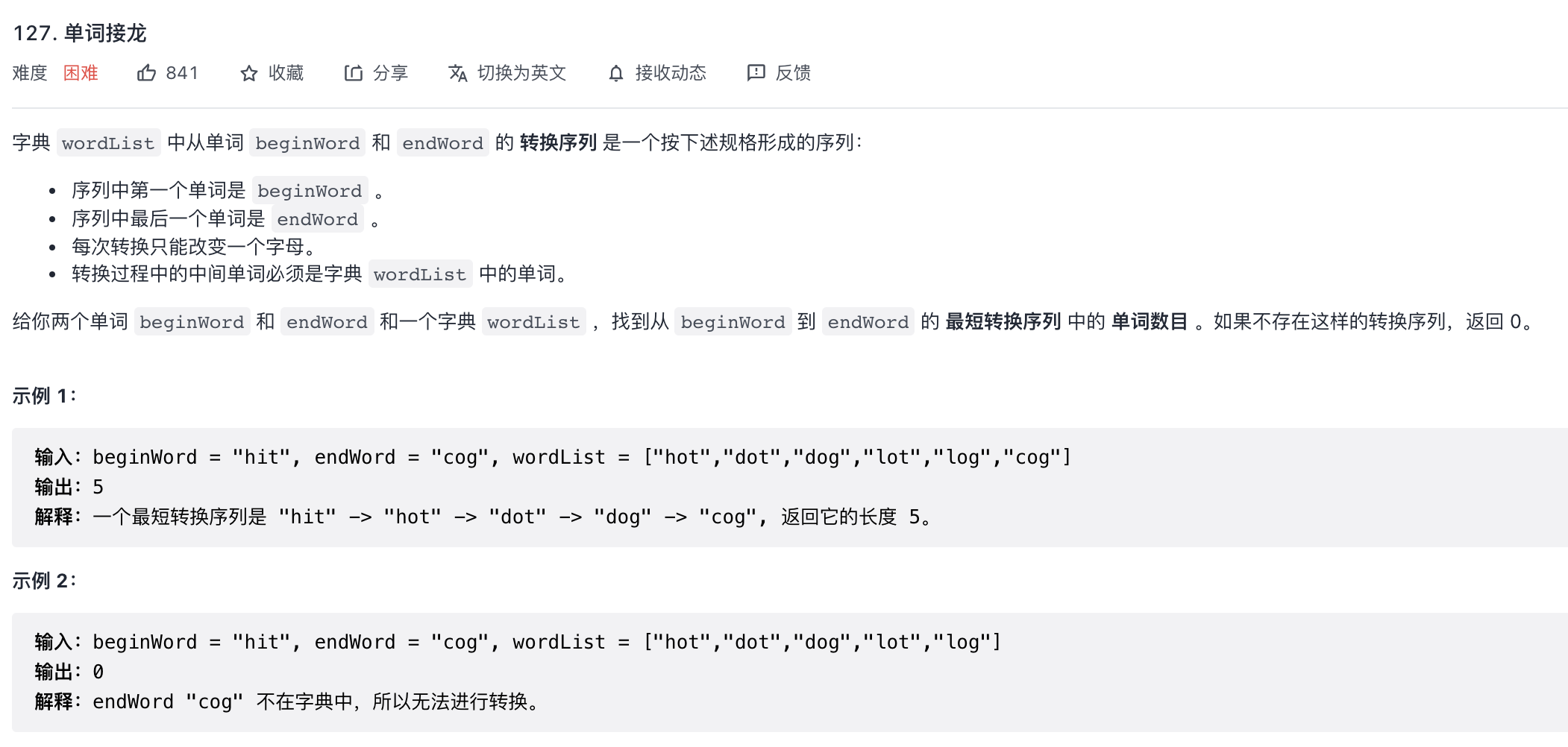
题目

类型：BFS
难度：困难

解题思路

• 无向图中两个顶点之间的最短路径的长度，可以通过广度优先遍历得到；
• 为什么 BFS 得到的路径最短？可以把起点和终点所在的路径拉直来看，两点之间线段最短；
• 已知目标顶点的情况下，可以分别从起点和目标顶点（终点）执行广度优先遍历，直到遍历的部分有交集，这是双向广度优先遍历的思想。

代码

import java.util.ArrayList;
import java.util.Collections;
import java.util.HashSet;
import java.util.List;
import java.util.Set;
public class Solution {
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        // 第 1 步：先将 wordList 放到哈希表里，便于判断某个单词是否在 wordList 里
        Set<String> wordSet = new HashSet<>(wordList);
        if (wordSet.size() == 0 || !wordSet.contains(endWord)) {
            return 0;
        }
        // 第 2 步：已经访问过的 word 添加到 visited 哈希表里
        Set<String> visited = new HashSet<>();
        // 分别用左边和右边扩散的哈希表代替单向 BFS 里的队列，它们在双向 BFS 的过程中交替使用
        Set<String> beginVisited = new HashSet<>();
        beginVisited.add(beginWord);
        Set<String> endVisited = new HashSet<>();
        endVisited.add(endWord);
        // 第 3 步：执行双向 BFS，左右交替扩散的步数之和为所求
        int step = 1;
        while (!beginVisited.isEmpty() && !endVisited.isEmpty()) {
            // 优先选择小的哈希表进行扩散，考虑到的情况更少
            if (beginVisited.size() > endVisited.size()) {
                Set<String> temp = beginVisited;
                beginVisited = endVisited;
                endVisited = temp;
            }
            // 逻辑到这里，保证 beginVisited 是相对较小的集合，nextLevelVisited 在扩散完成以后，会成为新的 beginVisited
            Set<String> nextLevelVisited = new HashSet<>();
            for (String word : beginVisited) {
                if (changeWordEveryOneLetter(word, endVisited, visited, wordSet, nextLevelVisited)) {
                    return step + 1;
                }
            }
            // 原来的 beginVisited 废弃，从 nextLevelVisited 开始新的双向 BFS
            beginVisited = nextLevelVisited;
            step++;
        }
        return 0;
    }
    /**
     * 尝试对 word 修改每一个字符，看看是不是能落在 endVisited 中，扩展得到的新的 word 添加到 nextLevelVisited 里
     *
     * @param word
     * @param endVisited
     * @param visited
     * @param wordSet
     * @param nextLevelVisited
     * @return
     */
    private boolean changeWordEveryOneLetter(String word, Set<String> endVisited,
                                             Set<String> visited,
                                             Set<String> wordSet,
                                             Set<String> nextLevelVisited) {
        char[] charArray = word.toCharArray();
        for (int i = 0; i < word.length(); i++) {
            char originChar = charArray[i];
            for (char c = 'a'; c <= 'z'; c++) {
                if (originChar == c) {
                    continue;
                }
                charArray[i] = c;
                String nextWord = String.valueOf(charArray);
                if (wordSet.contains(nextWord)) {
                    if (endVisited.contains(nextWord)) {
                        return true;
                    }
                    if (!visited.contains(nextWord)) {
                        nextLevelVisited.add(nextWord);
                        visited.add(nextWord);
                    }
                }
            }
            // 恢复，下次再用
            charArray[i] = originChar;
        }
        return false;
    }
}