题目

类型：DFS

解题思路

用 s 代指 source，用 t 代指 target，用 n 来代指 blocked 大小。

整理题意为：在一个足够大的空间里，有少数的障碍物，问两点是否连通。
当两个点中的任意一点被障碍物围住时，两点将无法连通。
一个很容易想到的思路是：从 s 跑一遍 BFS，然后从 t 跑一遍 BFS，同时设定一个最大访问点数量 MAX，若从两者出发能够访问的点数量都能超过 MAX，说明两点均没有被围住，最终必然会联通。

考虑如何敲定 MAX 的取值范围？直观感受，MAX 应该是一个与 blocked 大小相关的数。
但第一反应还是想从单秒计算量上界进行反推，两边 BFS 的复杂度均为 O(max)，因此直接设定 MAX = 1e5 应该是比较合适的。
更小的 MAX 需要证明：在给定数量障碍物的前提下，障碍物所能围成的最大面积为多少。
首先，容易想到：任何一条封闭图形的直边都可以通过调整为斜边来围成更大的面积：

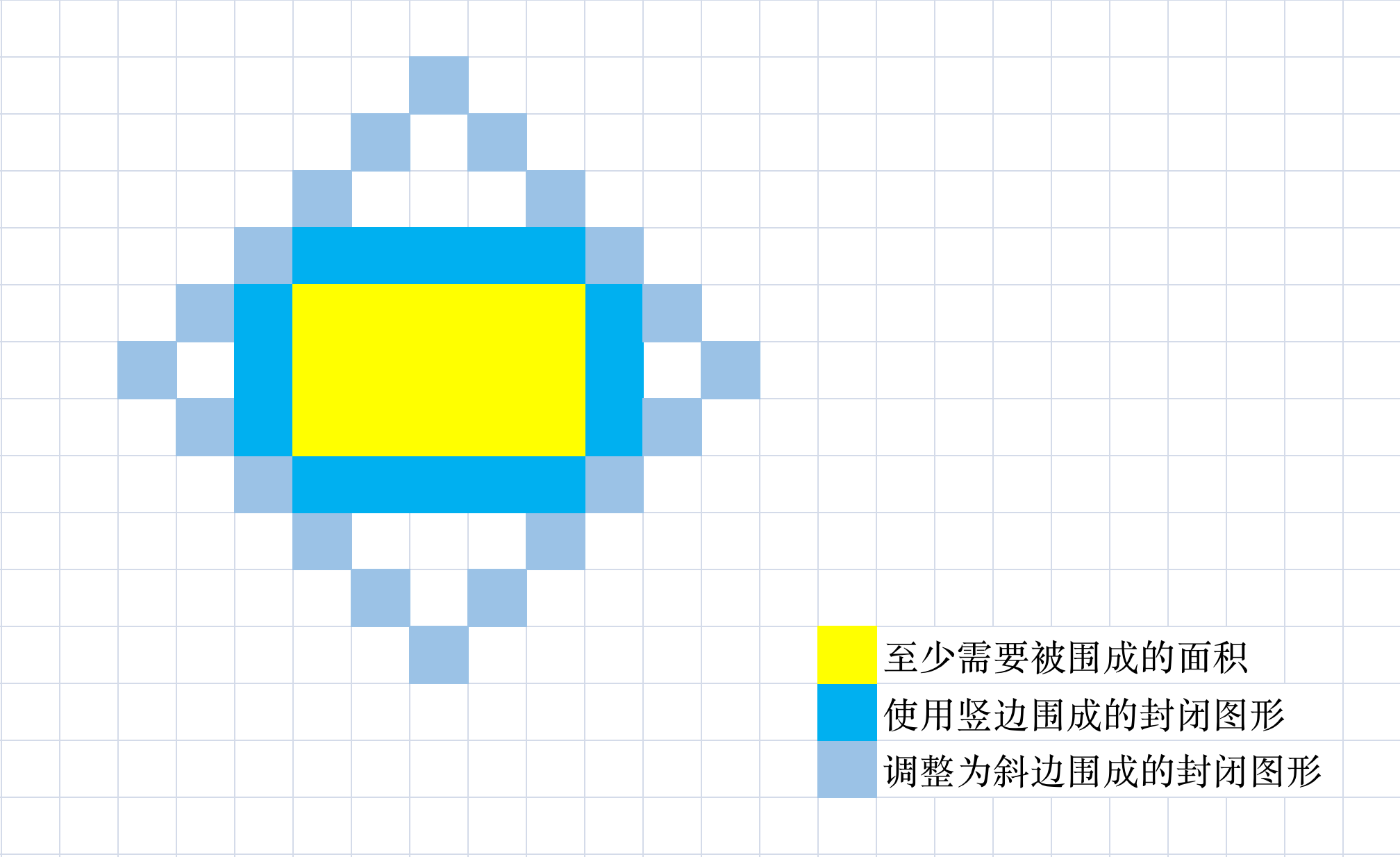
组成封闭图形的边不可能有直边，同时由于是封闭图形，因此斜边直接必然是单点衔接，而不可能是平行（无法封闭）。
同时，想要达到最大面积，应当尽可能利用边界作为围成图形的某些边。
利用边界所能围成的最大封面图形 可以是「由边界提供两边，障碍物提供一边的三角形」。
如果不是该形状，则可以通过调整障碍物的直边为一条完整的斜边，来组成封闭三角形，围成面积不会变小：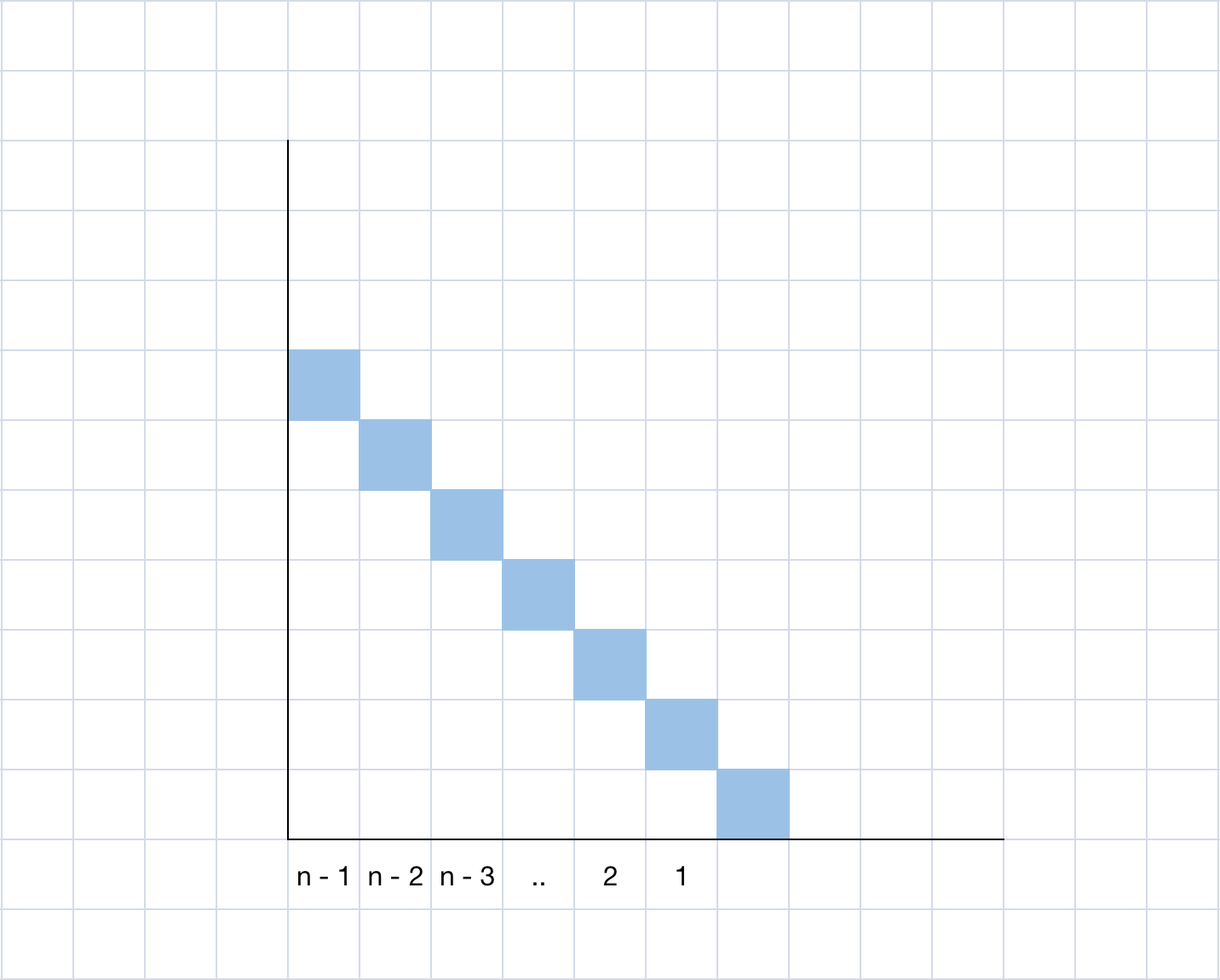

给定 n 的情况下，根据「等差数列求和」可知，最大所能围成的面积为
因此如果从 s 和 tt 出发，能够访问的点数超过 个，那么两点并没有被围住，必然联通。
最后，为了在 BFS 过程中记录某些点被访问过，可以通过计算某个位置哈希值（数值）来实现。

代码

class Solution {
    int EDGE = (int)1e6, MAX = (int)1e5;
    long BASE = 131L;
    Set<Long> set = new HashSet<>();
    int[][] dir = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
    public boolean isEscapePossible(int[][] blocked, int[] s, int[] t) {
        for (int[] p : blocked) set.add(p[0] * BASE + p[1]);
        int n = blocked.length;
        MAX = n * (n - 1) / 2; // 可直接使用 1e5
        return check(s, t) && check(t, s);
    }
    boolean check(int[] a, int[] b) {
        Set<Long> vis = new HashSet<>();
        Deque<int[]> d = new ArrayDeque<>();
        d.addLast(a);
        vis.add(a[0] * BASE + a[1]);
        while (!d.isEmpty() && vis.size() <= MAX) {
            int[] poll = d.pollFirst();
            int x = poll[0], y = poll[1];
            if (x == b[0] && y == b[1]) return true;
            for (int[] di : dir) {
                int nx = x + di[0], ny = y + di[1];
                if (nx < 0 || nx >= EDGE || ny < 0 || ny >= EDGE) continue;
                long hash = nx * BASE + ny;
                if (set.contains(hash)) continue;
                if (vis.contains(hash)) continue;
                d.addLast(new int[]{nx, ny});
                vis.add(hash);
            }
        }
        return vis.size() > MAX;
    }
}