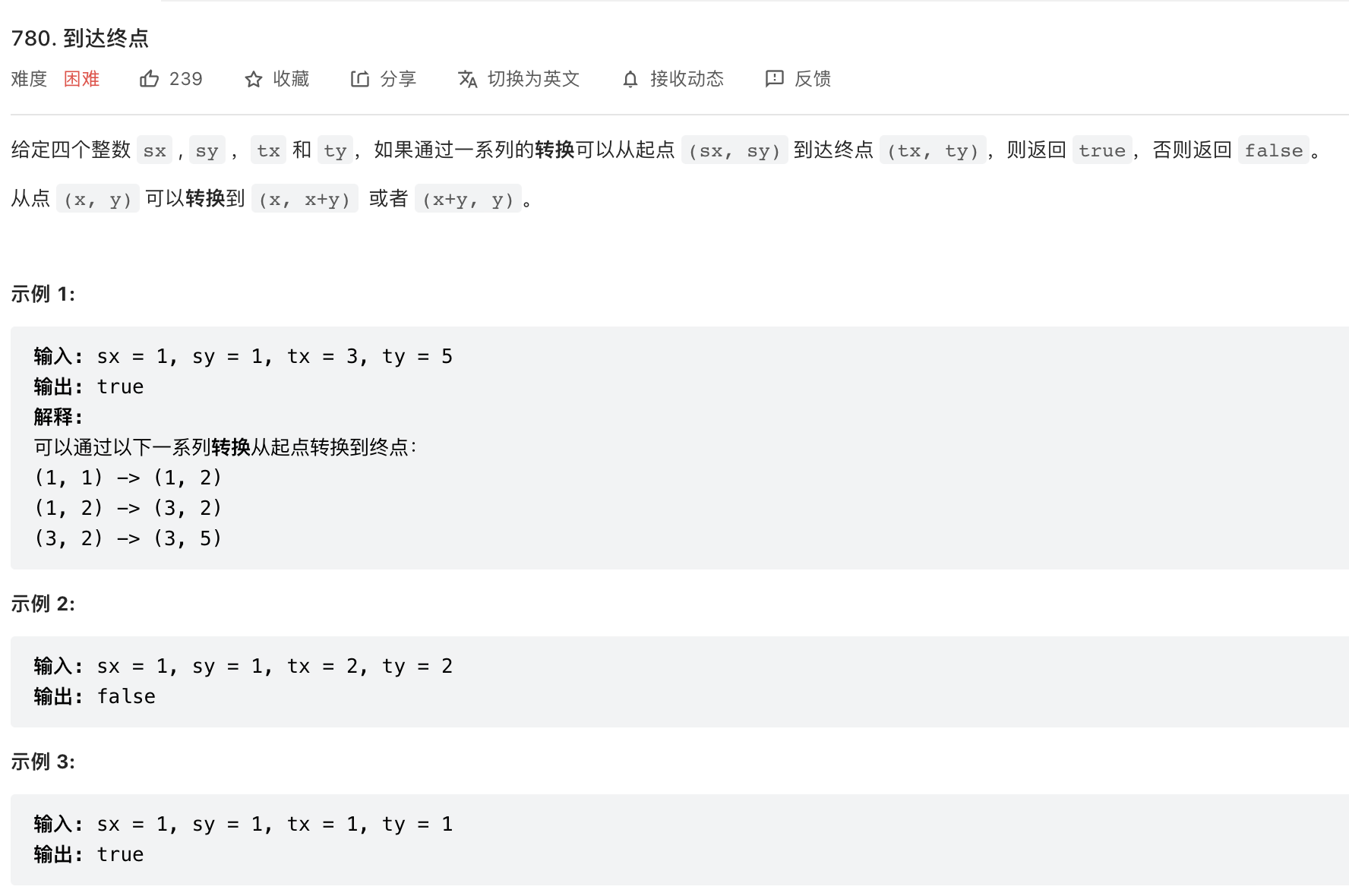
题目

类型：数学

解题思路

给定的 的数据范围为 （即均为正整数），且每次转换，只能将另外一维的数值累加到当前维，因此对于每一维的数值而言，随着转换次数的进行，呈（非严格）递增趋势，再结合起始值为正整数，可知在转换过程中均不会出现负数。
由此可以确定：总是取较大数减去较小数来进行反推
在某次反向转换中，如果有 tx<ty会将 (tx,ty) 转换为 (tx,ty−tx) ，减完仍有 tx<ty−tx ，该操作会继续进行，得到 (tx,ty−2*tx) ，其中 k 为转换次数。

代码

class Solution {
    public boolean reachingPoints(int sx, int sy, int tx, int ty) {
        while (sx < tx && sy < ty) {
            if (tx < ty) ty %= tx;
            else tx %= ty;
        }
        if (tx < sx || ty < sy) {
            return false;
        }
        return sx == tx ? (ty - sy) % tx == 0 : (tx - sx) % ty == 0;
    }
}