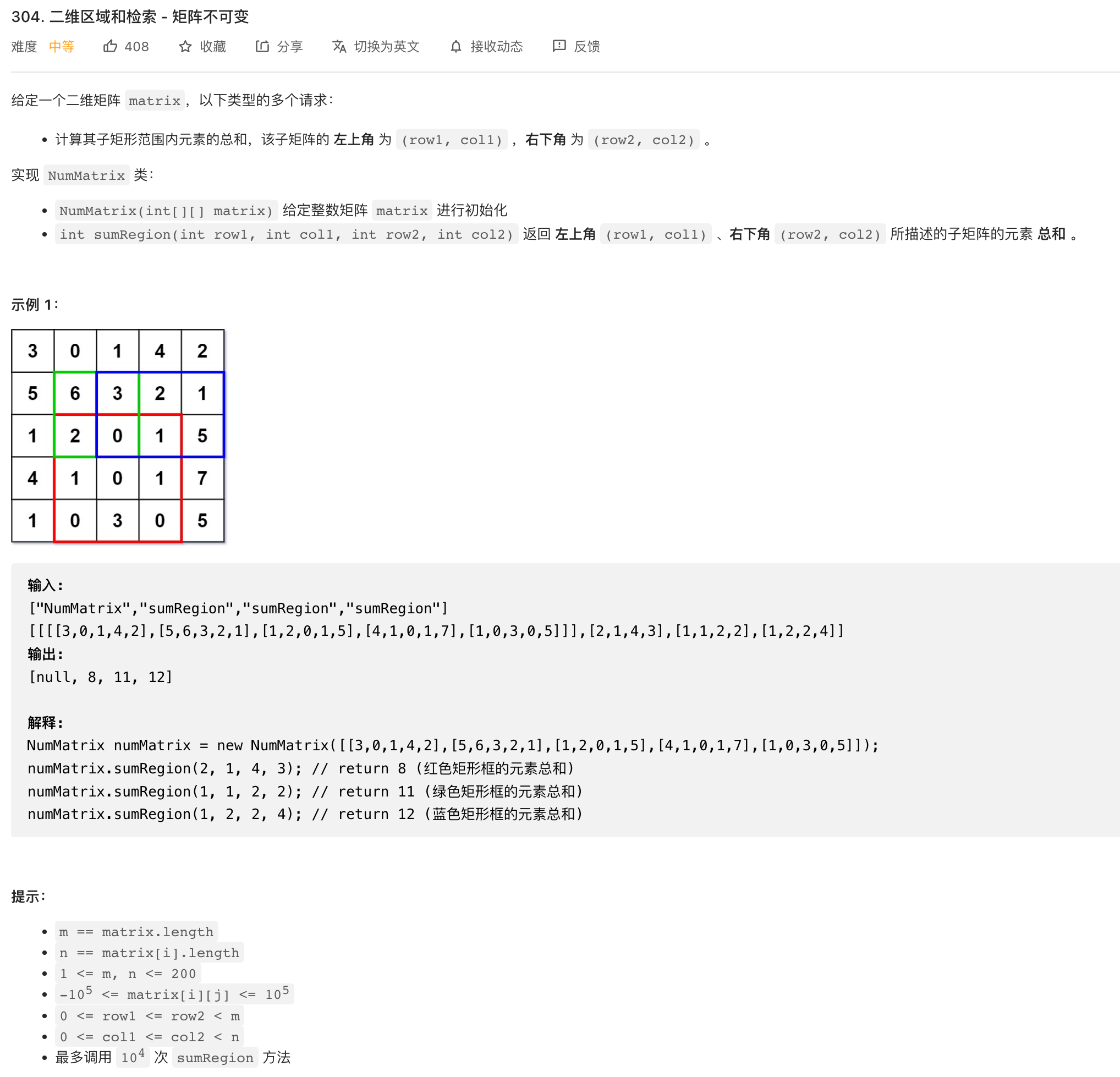
题目

类型：前缀和

image.png

解题思路

这题的思路和 303. 区域和检索 - 数组不可变 中一维数组中的前缀和问题是非常类似的，如下图：
image.png
如果我想计算红色的这个子矩阵的元素之和，可以用绿色矩阵减去蓝色矩阵减去橙色矩阵最后加上粉色矩阵，而绿蓝橙粉这四个矩阵有一个共同的特点，就是左上角就是 (0, 0) 原点。
那么我们可以维护一个二维 preSum 数组，专门记录以原点为顶点的矩阵的元素之和，就可以用几次加减运算算出任何一个子矩阵的元素和。

代码

  1. class NumMatrix {
  2.     // preSum[i][j] 记录矩阵 [0, 0, i, j] 的元素和
  3.     private int[][] preSum;
  5.     public NumMatrix(int[][] matrix) {
  6.         int m = matrix.length, n = matrix[0].length;
  7.         if (m == 0 || n == 0) return;
  8.         // 构造前缀和矩阵
  9.         preSum = new int[m + 1][n + 1];
  10.         for (int i = 1; i <= m; i++) {
  11.             for (int j = 1; j <= n; j++) {
  12.                 // 计算每个矩阵 [0, 0, i, j] 的元素和
  13.                 preSum[i][j] = preSum[i-1][j] + preSum[i][j-1] + matrix[i - 1][j - 1] - preSum[i-1][j-1];
  14.             }
  15.         }
  16.     }
  18.     // 计算子矩阵 [x1, y1, x2, y2] 的元素和
  19.     public int sumRegion(int x1, int y1, int x2, int y2) {
  20.         // 目标矩阵之和由四个相邻矩阵运算获得
  21.         return preSum[x2+1][y2+1] - preSum[x1][y2+1] - preSum[x2+1][y1] + preSum[x1][y1];
  22.     }
  23. }