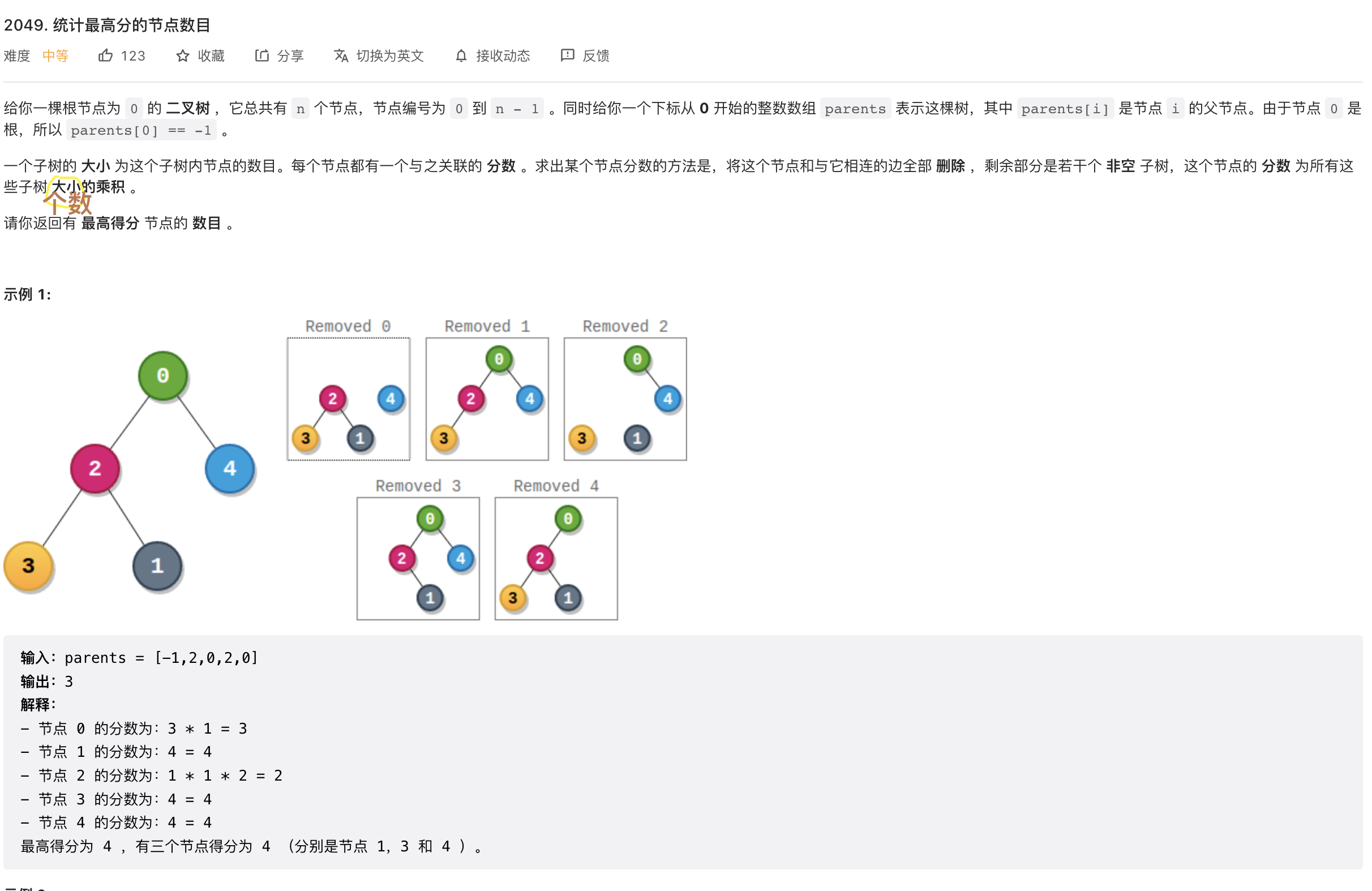
题目

类型：树

解题思路

1、假定该树为多叉树。
2、题目给定的 parents 数组仅支持快速查找某个节点的父节点，为了方便遍历整棵树，先使用「邻接表」将图（树）建起来。
使用 DFS 预处理出 f 数组，其中 f[i] 代表以节点 i 为根节点的子树所包含的节点数量。

3、如何计算「删除某个节点 x 后，剩余连通块的数量，以及每个连通块的节点数量」，根据节点 x 是否为根节点进行分情况讨论：

• 若 x 为根节点，删除后的连通块的数量为「x 的出边数量」，假定共有 k 条出边，根据题目定义，对应的 大小 为各个连通块的节点数量乘积：

• 若 x 不是根节点，删除后的连通块的数量为「x 的出边数量 + 1」，其中 1 代指「以 x 节点的父节点所在的整体连通块」。

假定节点 x 共有 k 条出边，根据题目定义，对应的 大小 为「(各个连通块的节点数量乘积) (x 节点的父节点所在的整体连通块大小)」，而「x 节点的父节点所在的整体连通块大小」，利用容斥原理可知为 f[root] - f[u] = n - f[u]，含义为「从原树中减掉以节点 x 为根节点的子树」的部分，即最终 大小 为：

代码

public class CountNodesWithTheHighestScore {
    static int N = 100010, M = N * 2;
    static int[] he = new int[N], e = new int[M], ne = new int[M];
    static int[] f = new int[N];
    int idx;  //成员变量idx 默认初始值0，对边进行编号
    //建邻接图
    void add(int a, int b) {
        e[idx] = b; //当前idx边指向的节点
        ne[idx] = he[a]; //下一条边 若为-1则表示没有下一个了
        he[a] = idx++; //头结点
    }
    public int countHighestScoreNodes(int[] parents) {
        Arrays.fill(he, -1);  //初始化让所有边都没有下一条
        int n = parents.length;  //节点数目
        for (int i = 1; i < n; i++) add(parents[i], i); //建图
        dfs(0);//从根节点开始dfs，在搜索过程中存储当前节点的子树节点数目（含当前节点）
        long max = 0; //最坑的一个点,使用int会溢出,必须使用long
        int ans = 0; //最高得分计数
        for (int x = 0; x < n; x++) {
            long cur = 1;
            //删除节点x
            for (int i = he[x]; i != -1; i = ne[i]) cur *= f[e[i]]; //累乘删除的左右子树数量
            if (x != 0) cur *= n - f[x]; //如果不是根节点，还要再把上方剩余子树的n - f[x]个节点数量相乘
            if (cur > max) {
                //比之前的乘积大就替换,并把数量置1
                max = cur; ans = 1;
            } else if (cur == max) {
                //跟之前的最大值一样大,则数量+1
                ans++;
            }
        }
        return ans;
    }
    //递归函数
    int dfs(int u) {
        int ans = 1;//因为是依据边访问点,说明有一定有一个节点,所以至少都是1
        for (int i = he[u]; i != -1; i = ne[i]) ans += dfs(e[i]);//把子树的数目加上来
        f[u] = ans;//存储以u为根节点的树的节点数目
        return ans;
    }
}