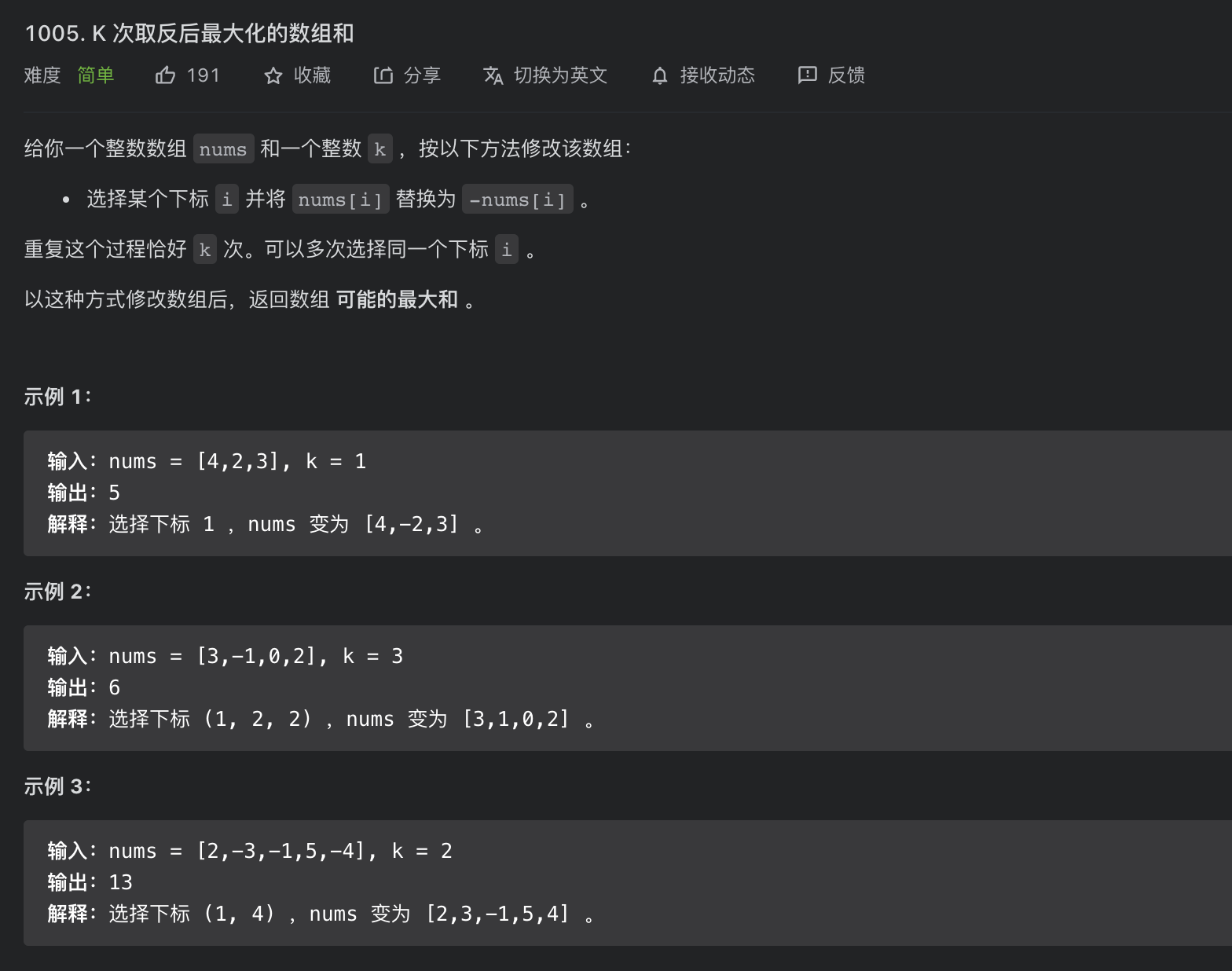
题目

类型：贪心

解题思路

1、由于希望数组的和尽可能大，因此应当总是修改负数，并且优先修改值最小的负数。因为将负数 −x 修改成 x 会使得数组的和增加 2x，所以这样的贪心操作是最优的。

2、当给定的 K 小于等于数组中负数的个数时，按照上述方法从小到大依次修改每一个负数即可。但如果 K 的值较大，那么不得不去修改非负数了。由于修改 0 对数组的和不会有影响，而修改正数会使得数组的和减小，因此：

• 如果数组中存在 0，那么可以对它进行多次修改，直到把剩余的修改次数用完；
• 如果数组中不存在 0 并且剩余的修改次数是偶数，由于对同一个数修改两次等价于不进行修改，因此也可以在不减小数组的和的前提下，把修改次数用完；
• 如果数组中不存在 0 并且剩余的修改次数是奇数，那么必然需要使用单独的一次修改将一个正数变为负数（剩余的修改次数为偶数，就不会减小数组的和）。为了使得数组的和尽可能大，就选择那个最小的正数。

需要注意的是，在之前将负数修改为正数的过程中，可能出现了（相较于原始数组中最小的正数）更小的正数，这一点不能忽略。

代码

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        Map<Integer, Integer> freq = new HashMap<Integer, Integer>();
        for (int num : nums) {
            freq.put(num, freq.getOrDefault(num, 0) + 1);
        }
        int ans = Arrays.stream(nums).sum();
        for (int i = -100; i < 0; ++i) {
            if (freq.containsKey(i)) {
                int ops = Math.min(k, freq.get(i));
                ans += (-i) * ops * 2;
                freq.put(i, freq.get(i) - ops);
                freq.put(-i, freq.getOrDefault(-i, 0) + ops);
                k -= ops;
                if (k == 0) {
                    break;
                }
            }
        }
        if (k > 0 && k % 2 == 1 && !freq.containsKey(0)) {
            for (int i = 1; i <= 100; ++i) {
                if (freq.containsKey(i)) {
                    ans -= i * 2;
                    break;
                }
            }
        }
        return ans;
    }
}