题目

类型：数组

解题思路

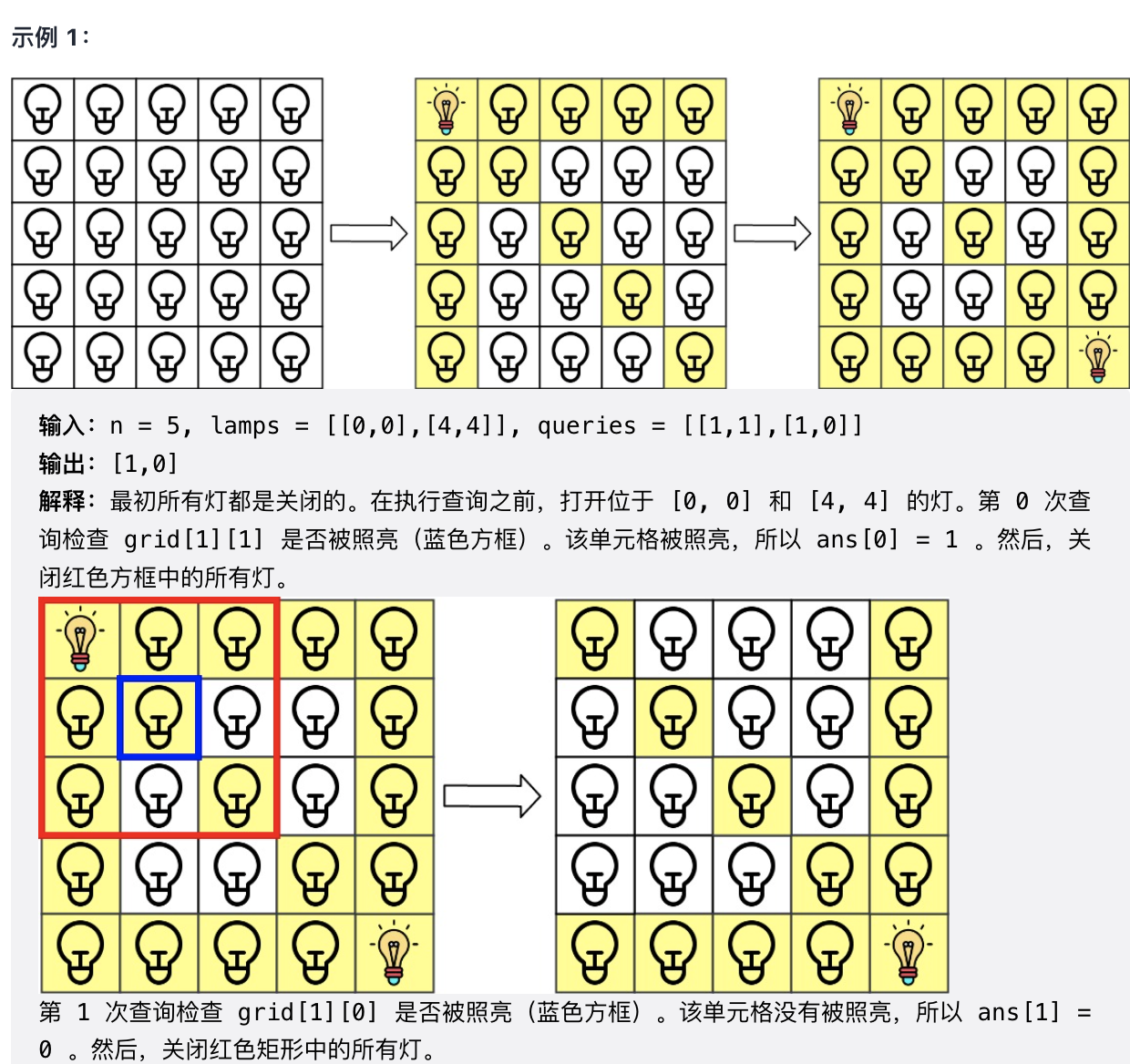
棋盘大小的数据范围为 ，硬模拟「亮灯」的操作必然会 TLE，而 lamps 和 queries 数据范围为 20000 是一个较为常见的突破口。

由于点亮每一盏灯，可以使得当前 行、列 和 对角线 的位置被照亮，行列可直接使用棋盘坐标的 (x, y) 来代指，而对角线则可以使用「截距」来进行代指，即使用 x + y 和 x - y 进行代指。

分别使用四个「哈希表」row、col、left 和 right 来记录 行、列 和 对角线 的点亮情况（key 为线编号，value 为点亮次数）。

这样我们可以在 O(1) 的复杂度处理掉所有的 lamps[i] ，某个位置被照亮的充要条件为：「当前位置所在行被点亮」或「当前位置所在列被点亮」或「当前位置所处的对角线被点亮」。

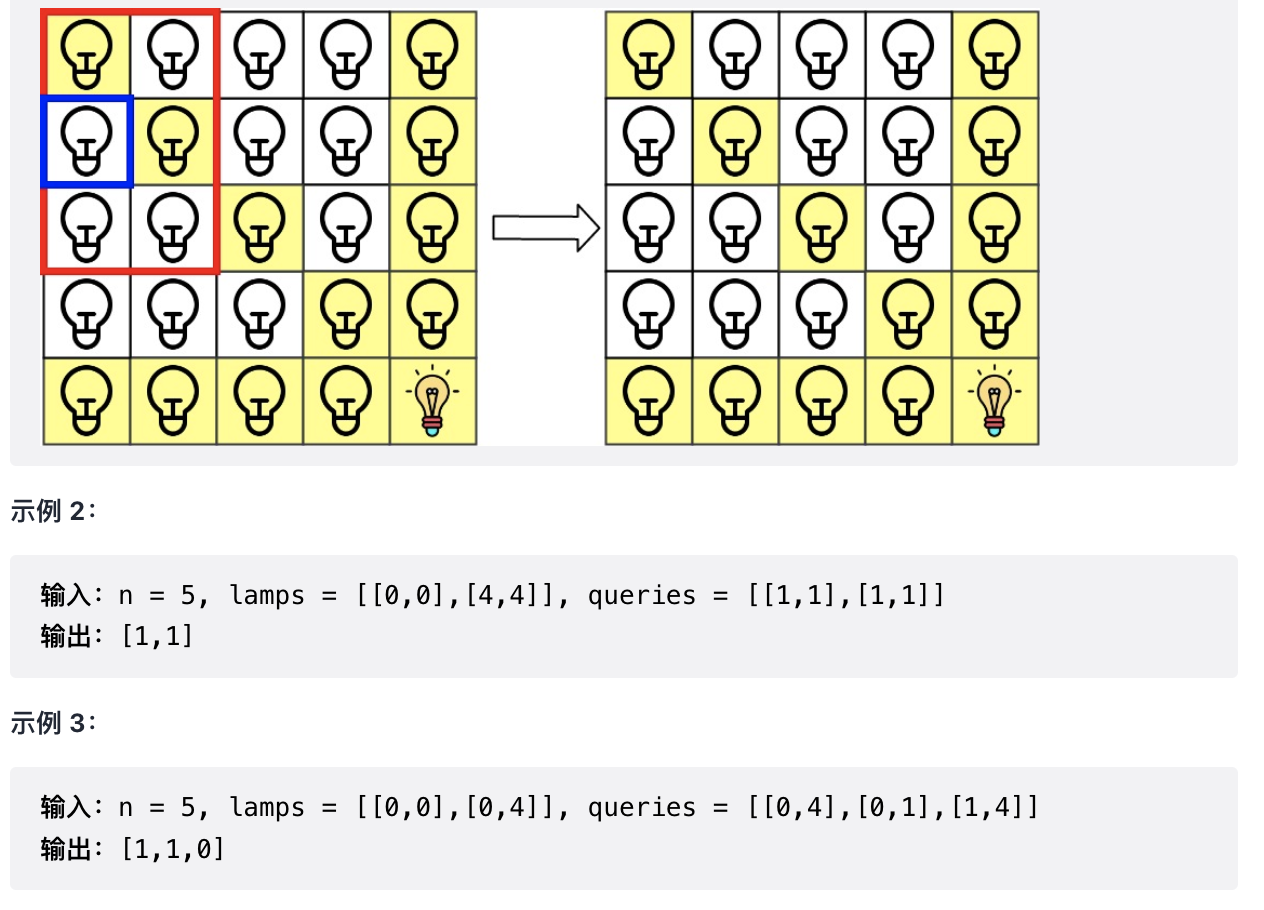
同时，由于每次查询后要进行「灭灯」操作（注意：灭灯只能灭有灯的位置，而不是灭有光的位置 ），因此我们还需要另外记录每个灯的位置，可以使用利用「二维转一维」的技巧进行编号：idx = x * n + y ，并使用 HashSet 进行记录（忽略重复的 lamps[i] ）。

由于询问次数最多为 20000，因此直接在查询完成后模拟「灭灯」即可（访问自身及相邻格子，共 9 个），计算量为 以内，可以接受。若某个位置存在灯，将其从 HashSet 中移除，并更新对应线的点亮情况。

代码

class Solution {
    int[][] dirs = new int[][]{{0,0},{0,-1},{0,1},{-1,0},{-1,-1},{-1,1},{1,0},{1,-1},{1,1}};
    public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {
        long N = n;
        Map<Integer, Integer> row = new HashMap<>(), col = new HashMap<>();
        Map<Integer, Integer> left = new HashMap<>(), right = new HashMap<>();
        Set<Long> set = new HashSet<>();
        for (int[] l : lamps) {
            int x = l[0], y = l[1];
            int a = x + y, b = x - y;
            if (set.contains(x * N + y)) continue;
            increment(row, x); increment(col, y);
            increment(left, a); increment(right, b);
            set.add(x * N + y);
        }
        int m = queries.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; i++) {
            int[] q = queries[i];
            int x = q[0], y = q[1];
            int a = x + y, b = x - y;
            if (row.containsKey(x) || col.containsKey(y) || left.containsKey(a) || right.containsKey(b)) ans[i] = 1;
            for (int[] d : dirs) {
                int nx = x + d[0], ny = y + d[1];
                int na = nx + ny, nb = nx - ny;
                if (nx < 0 || nx >= n || ny < 0 || ny >= n) continue;
                if (set.contains(nx * N + ny)) {
                    set.remove(nx * N + ny);
                    decrement(row, nx); decrement(col, ny);
                    decrement(left, na); decrement(right, nb);
                }
            }
        }
        return ans;
    }
    void increment(Map<Integer, Integer> map, int key) {
        map.put(key, map.getOrDefault(key, 0) + 1);
    }
    void decrement(Map<Integer, Integer> map, int key) {
        if (map.get(key) == 1) map.remove(key);
        else map.put(key, map.get(key) - 1);
    }
}