Number类型

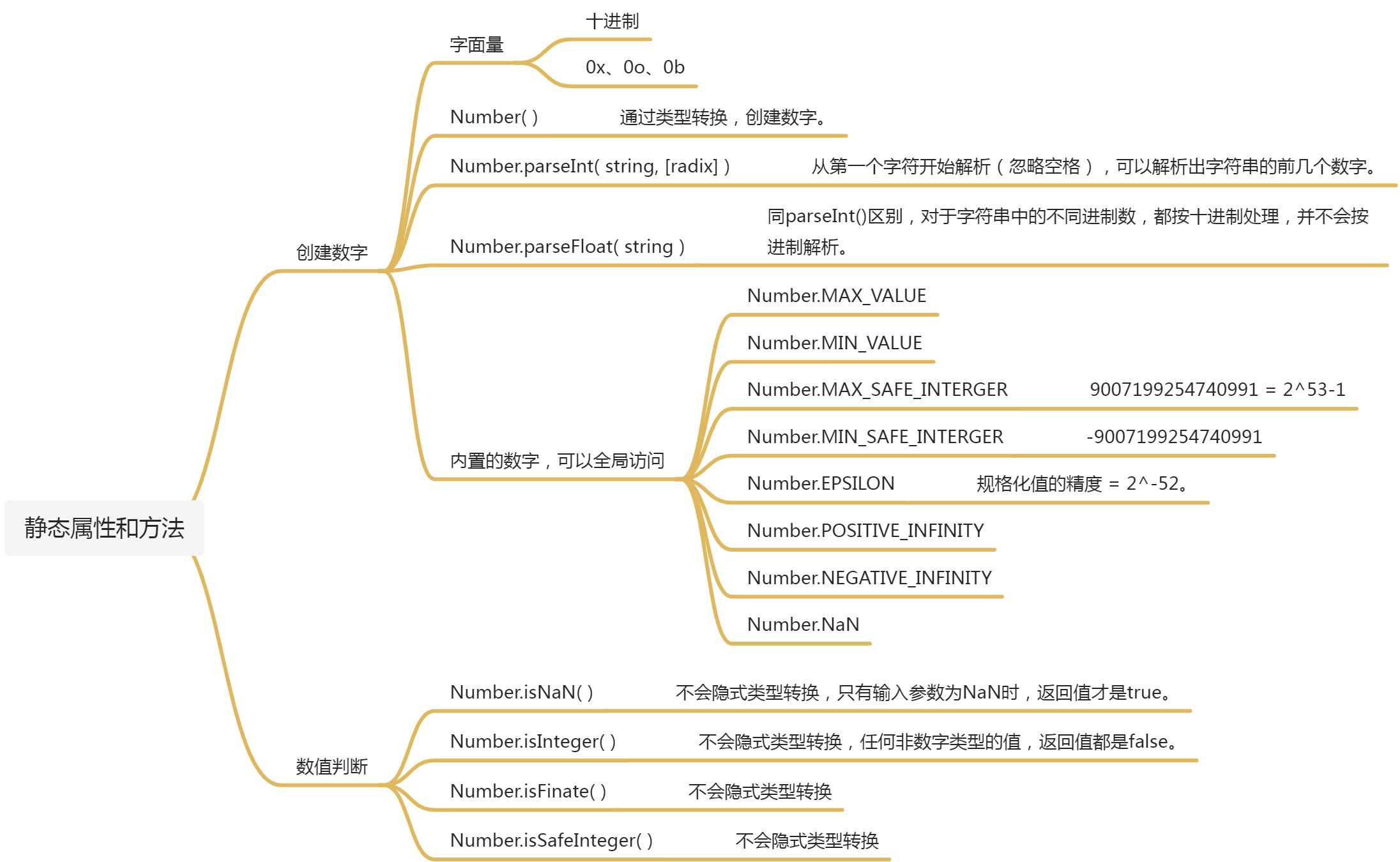
静态属性和方法

Number类型 - 图2

实例化对象

Number类型 - 图3

原型对象

Number类型 - 图4 :::info

  • 慎用这些方法，因为浮点数的表示并不准确，在四舍五入时，有时会出错。
  • 这些方法的返回值不是数字而是字符串。 :::

    注释说明

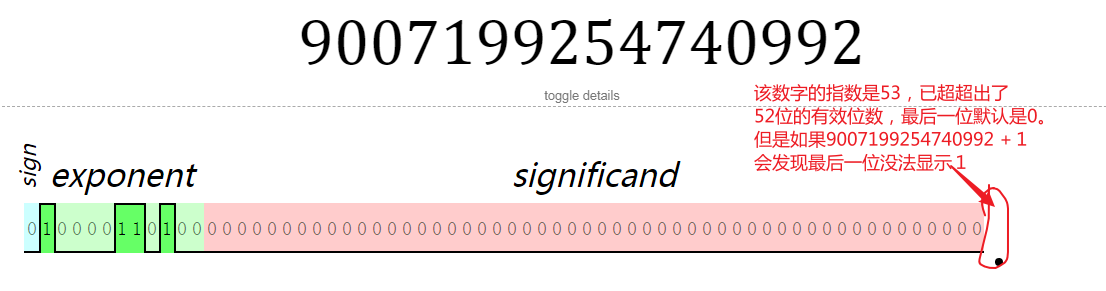
    MAX_SAFE_INTERGER

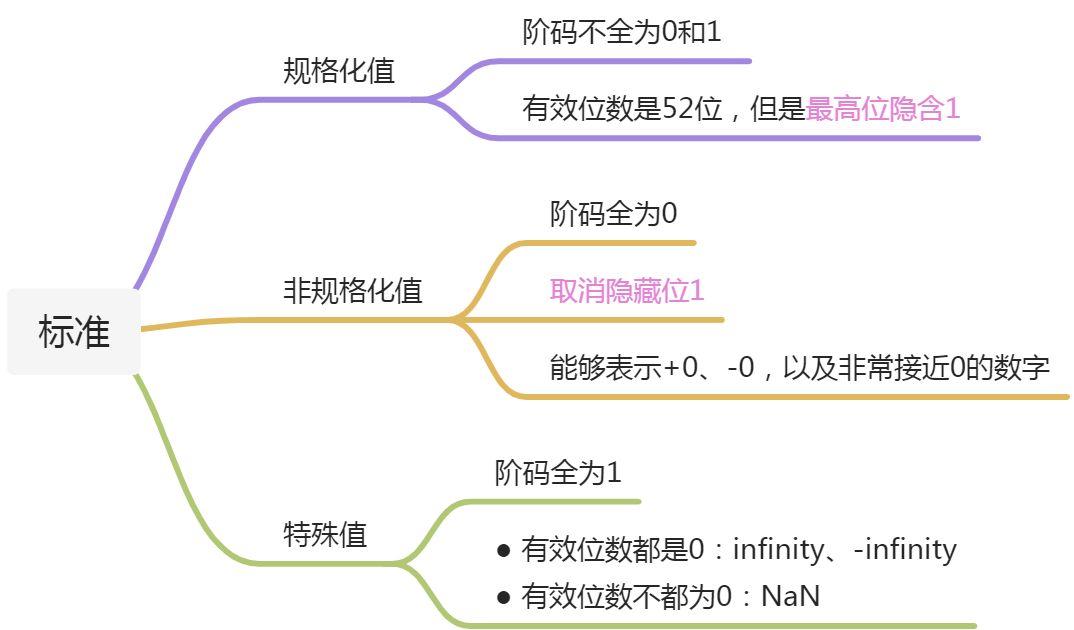
    根据IEEE754标准，有效表示位数是52位，因此规格化数的阶码数只能在0~52之间。如果阶码大于52，溢出的位数只能算作是0。
    image.png
    image.png :::info 位数溢出明显缺点无法连续表示整数，例如：9007199254740992 + 1 = 9007199254740992。 :::

    EPSILON

    image.png

    IEEE754

    浮点数及其运算标准。在计算机科学中，浮点数是通过小数点的浮动位置，来确定数值的整数部分和小数部分。

    image.png

    :::info 如果整数部分越大，能够精确表示的小数位数就越小。因此常说大约能够精确到几位数字。 :::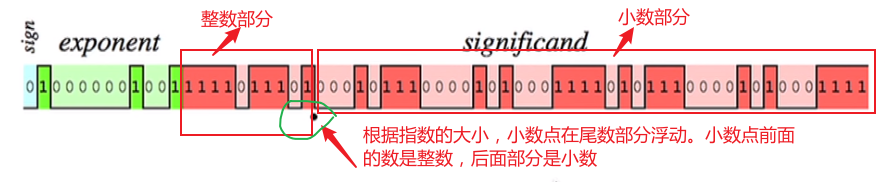

    实数

    在数学领域里，实数可以使用小数表示，并且可以在数轴上找到与之对应的点。但是无法通过有限小数表示所有的数，产生无限小数的概念。 :::info 计算机只能表示有限的二进制数字。同时浮点数由于小数精度的原因，运算时容易产生误差。 :::

    标准

    Number类型 - 图9

    参考

    https://blog.csdn.net/ixygj197875/article/details/79117229 Number.EPSILON
    https://www.bilibili.com/read/cv3129825/ 思考无限循环小数
    https://stackoverflow.com/questions/19800415/why-does-ieee-754-reserve-so-many-nan-values 为什么NaN有如此多的数值表示
    https://www.youtube.com/watch?v=8afbTaA-gOQ 十进制小数如何转化为二进制的浮点数
    http://bartaz.github.io/ieee754-visualization/ 双精度浮点数可视化网站