方案1: 借助redis的Set
具体实现代码
缺点
- 需要频繁连接Redis
2. 如果数据量过大, 对redis的内存也是一种压力方案2: 使用Flink的MapState
具体实现代码
参考:案例5:MapState缺点
- 如果数据量过大, 状态后端最好选择RocksDBStateBackend
2. 如果数据量过大, 对存储也有一定压力方案3: 使用布隆过滤器
布隆过滤器可以大大减少存储的数据的数据量布隆过滤器
为什么需要布隆过滤器
如果想判断一个元素是不是在一个集合里,一般想到的是将集合中所有元素保存起来,然后通过比较确定。链表、树、散列表(又叫哈希表,Hash table)等等数据结构都是这种思路。
但是随着集合中元素的增加,我们需要的存储空间越来越大。同时检索速度也越来越慢,上述三种结构的检索时间复杂度分别为。
布隆过滤器即可以解决存储空间的问题, 又可以解决时间复杂度的问题.
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。基本概念
布隆过滤器(Bloom Filter,下文简称BF)由Burton Howard Bloom在1970年提出,是一种空间效率高的概率型数据结构。它专门用来检测集合中是否存在特定的元素。
它实际上是一个很长的二进制向量和一系列随机映射函数。实现原理
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。
BF是由一个长度为m比特的位数组(bit array)与k个哈希函数(hash function)组成的数据结构。位数组均初始化为0,所有哈希函数都可以分别把输入数据尽量均匀地散列。
当要插入一个元素时,将其数据分别输入k个哈希函数,产生k个哈希值。以哈希值作为位数组中的下标,将所有k个对应的比特置为1。
当要查询(即判断是否存在)一个元素时,同样将其数据输入哈希函数,然后检查对应的k个比特。如果有任意一个比特为0,表明该元素一定不在集合中。如果所有比特均为1,表明该集合有(较大的)可能性在集合中。为什么不是一定在集合中呢?因为一个比特被置为1有可能会受到其他元素的影响(hash碰撞),这就是所谓“假阳性”
(false positive)。相对地,“假阴性”(false negative)在BF中是绝不会出现的。
下图示出一个m=18, k=3的BF示例。集合中的x、y、z三个元素通过3个不同的哈希函数散列到位数组中。当查询元素w时,因为有一个比特为0,因此w不在该集合中。
优点
- 不需要存储数据本身,只用比特表示,因此空间占用相对于传统方式有巨大的优势,并且能够保密数据;
2. 时间效率也较高,插入和查询的时间复杂度均为, 所以他的时间复杂度实际是
3. 哈希函数之间相互独立,可以在硬件指令层面并行计算。缺点
- 存在假阳性的概率,不适用于任何要求100%准确率的情境;
2. 只能插入和查询元素,不能删除元素,这与产生假阳性的原因是相同的。我们可以简单地想到通过计数(即将一个比特扩展为计数值)来记录元素数,但仍然无法保证删除的元素一定在集合中。使用场景
所以,BF在对查准度要求没有那么苛刻,而对时间、空间效率要求较高的场合非常合适.
另外,由于它不存在假阴性问题,所以用作“不存在”逻辑的处理时有奇效,比如可以用来作为缓存系统(如Redis)的缓冲,防止缓存穿透。假阳性概率的计算(失败概率)
假阳性的概率其实就是一个不在的元素,被k个函数函数散列到的k个位置全部都是1的概率。可以按照如下的步骤进行计算: p = f(m,n,k)
其中各个字母的含义:
1. n :放入BF中的元素的总个数;
2. m:BF的总长度,也就是bit数组的个数
3. k:哈希函数的个数;
4. p:表示BF将一个不在其中的元素错判为在其中的概率,也就是false positive的概率;
A. BF中的任何一个bit在第一个元素的第一个hash函数执行完之后为 0的概率是:
B. BF中的任何一个bit在第一个元素的k个hash函数执行完之后为 0的概率是: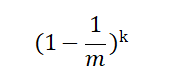
C. BF中的任何一个bit在所有的n元素都添加完之后为 0的概率是:
D. BF中的任何一个bit在所有的n元素都添加完之后为 1的概率是:
E. 一个不存在的元素被k个hash函数映射后k个bit都是1的概率是:
结论:在哈数函数个数k一定的情况下
1. 比特数组m长度越大, p越小, 表示假阳性率越低
2. 已插入的元素个数n越大, p越大, 表示假阳性率越大
经过各种数学推导:
对于给定的m和n,使得假阳性率(误判率)最小的k通过如下公式定义:
使用布隆过滤器实现去重
Flink已经内置了布隆过滤器的实现(使用的是google的Guava)
| public class Flink02UV_BoomFilter **{
public static void main(String[] args) throws Exception {
**StreamExecutionEnvironment env = StreamExecutionEnvironment._getExecutionEnvironment();
_// 创建WatermarkStrategy<br /> _WatermarkStrategy<UserBehavior> wms = WatermarkStrategy<br /> .<UserBehavior>_forBoundedOutOfOrderness_**_(_**Duration._ofSeconds_**_(_**5**_))<br /> _**.withTimestampAssigner**_(_new **SerializableTimestampAssigner<UserBehavior>**_() {<br /> _**@Override<br /> **public long **extractTimestamp**_(_**UserBehavior element, **long **recordTimestamp**_) {<br /> _return **element.getTimestamp**_() _*** 1000L;<br /> **_}<br /> })_**;env<br /> .readTextFile**_(_"input/UserBehavior.csv"_)<br /> _**.map**_(_**line -> **_{ _**_// 对数据切割, 然后封装到POJO中<br /> _String**_[] _**split = line.split**_(_","_)_**;<br /> **return new **UserBehavior**_(_**Long._valueOf_**_(_**split**_[_**0**_])_**, Long._valueOf_**_(_**split**_[_**1**_])_**, Integer._valueOf_**_(_**split**_[_**2**_])_**, split**_[_**3**_]_**, Long._valueOf_**_(_**split**_[_**4**_]))_**;<br /> **_})<br /> _**.filter**_(_**behavior -> **"pv"**.equals**_(_**behavior.getBehavior**_())) _**_//过滤出pv行为<br /> _.assignTimestampsAndWatermarks**_(_**wms**_)<br /> _**.keyBy**_(_**UserBehavior::getBehavior**_)<br /> _**.window**_(_**TumblingEventTimeWindows._of_**_(_**Time._minutes_**_(_**60**_)))<br /> _**.process**_(_new **ProcessWindowFunction<UserBehavior, String, String, TimeWindow>**_() {_private **ValueState<Long> **countState**;<br /> **private **ValueState<BloomFilter<Long>> **bfState**;@Override<br /> **public void **open**_(_**Configuration parameters**_) _throws **Exception **_{<br /> _countState **= getRuntimeContext**_()_**.getState**_(_new **ValueStateDescriptor<Long>**_(_"countState"**, Long.**class_))_**;**bfState **= getRuntimeContext**_()<br /> _**.getState**_(_new **ValueStateDescriptor<BloomFilter<Long>>**_(_"bfState"**, TypeInformation._of_**_(_new **TypeHint<BloomFilter<Long>>**_() {})<br /> )<br /> )_**;**_}_**@Override<br /> **public void **process**_(_**String key,<br /> Context context,<br /> Iterable<UserBehavior> elements, Collector<String> out**_) _throws **Exception **_{<br /> _countState**.update**_(_**0L**_)_**;_// 在状态中初始化一个布隆过滤器<br /> // 参数1: 漏斗, 存储的类型<br /> // 参数2: 期望插入的元素总个数<br /> // 参数3: 期望的误判率(假阳性率)<br /> _BloomFilter<Long> bf = BloomFilter._create_**_(_**Funnels._longFunnel_**_()_**, 1000000, 0.001**_)_**;<br /> **bfState**.update**_(_**bf**_)_**;<br /> <br /> **for _(_**UserBehavior behavior : elements**_) {<br /> _**_// 查布隆<br /> _**if _(_**!**bfState**.value**_()_**.mightContain**_(_**behavior.getUserId**_())) {<br /> _**_// 不存在计数+1<br /> _**countState**.update**_(_countState**.value**_() _**+ 1L**_)_**;<br /> _// 记录这个用户di, 表示来过<br /> _**bfState**.value**_()_**.put**_(_**behavior.getUserId**_())_**;<br /> **_}<br /> }<br /> _**out.collect**_(_"窗口: " **+ context.window**_() _**+ **" 的uv是: " **+ **countState**.value**_())_**;<br /> **_}<br /> })<br /> _**.print**_()_**;<br /> env.execute**_()_**;<br /> **_}<br />}_** |
| —- |

