本文以《漫画统计学》学习记录，梳理统计学的基础知识，供数据分析领域的同学参考。
0、统计学的分类
统计学可以分为推断统计学和描述统计学。
- 推断统计学：从样本的信息推测总体的状况
- 描述统计学：就是为了简单的表示数据的状况，而非推测。比如算某个总体的均值和标准差
一、数据分类
分类数据（不可测量的数据）
比如性别、是否满意（不满意，一般，比较满意，非常满意等）数值数据（可测量的数据）
比如年龄，金额
判定标准：选项之间的间隔相等
二、数据的整体状态（数值类数据）
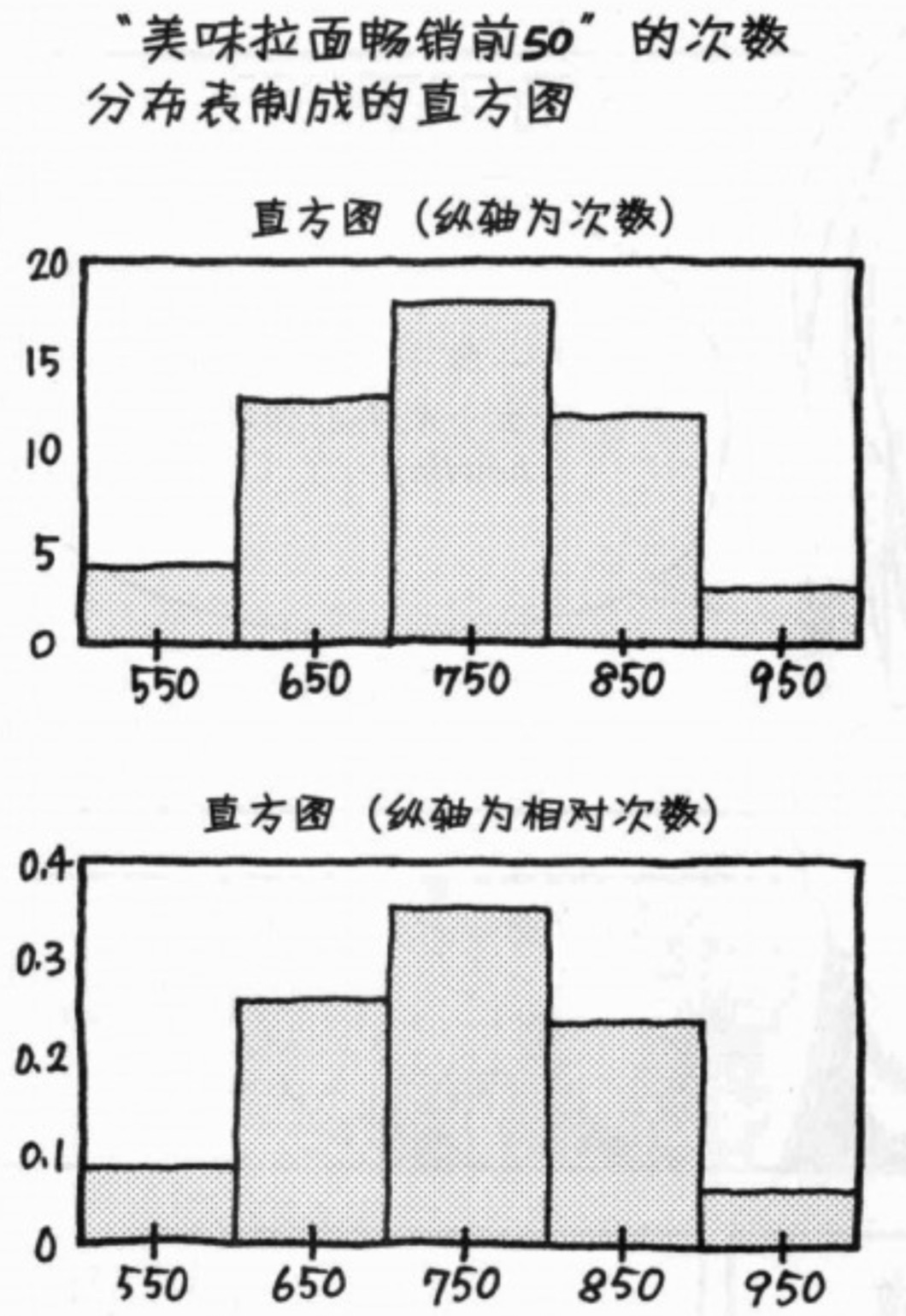
次数分布图
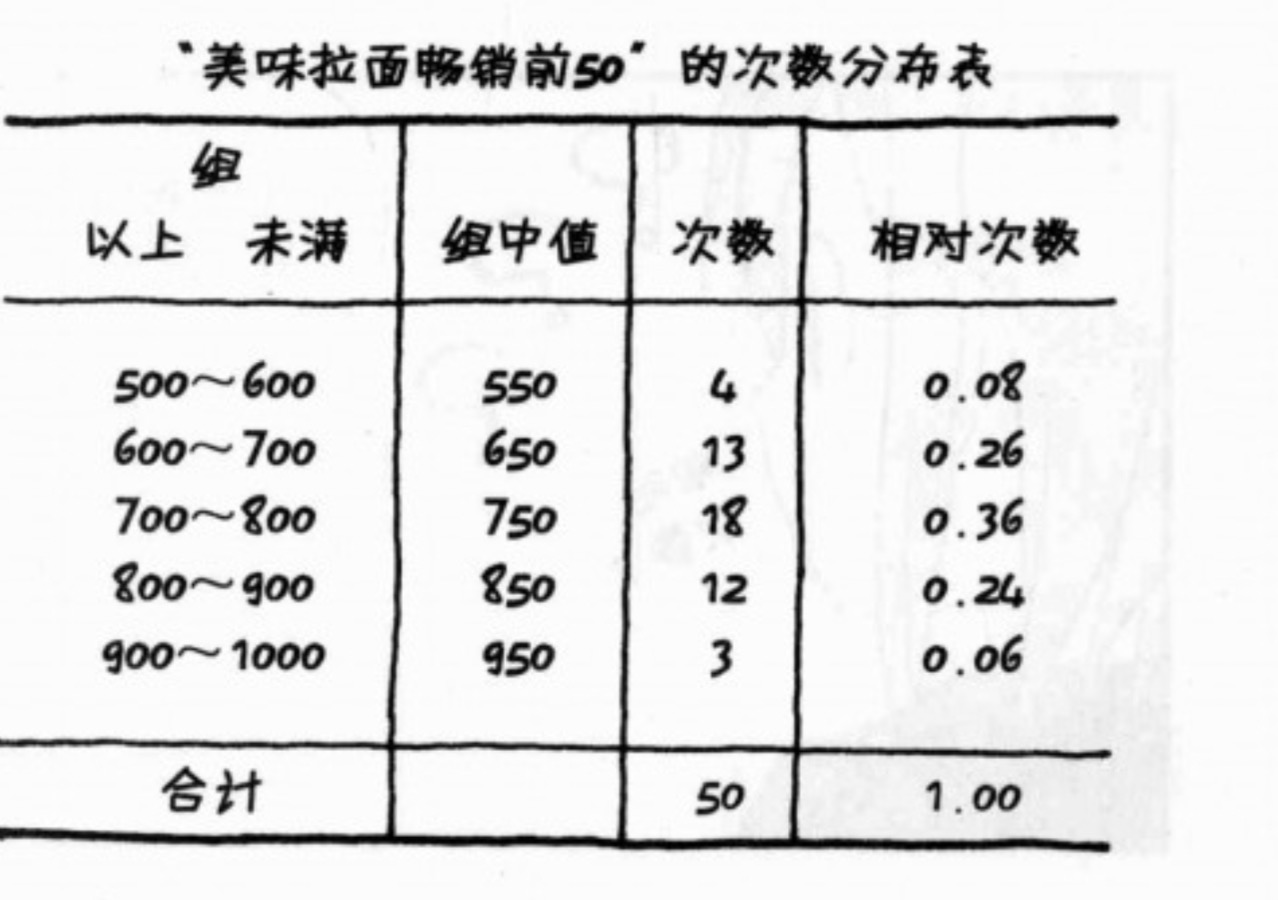
次数分布图是将原始数据进行分组统计每组次数。以上表格采用柱状图表示更加直观。
直方图（柱状图）
平均数
中位数
为什么要有中位数。以下是保龄球大赛的结果数据，仅用平均数表示队中每个人的大概得分不合理。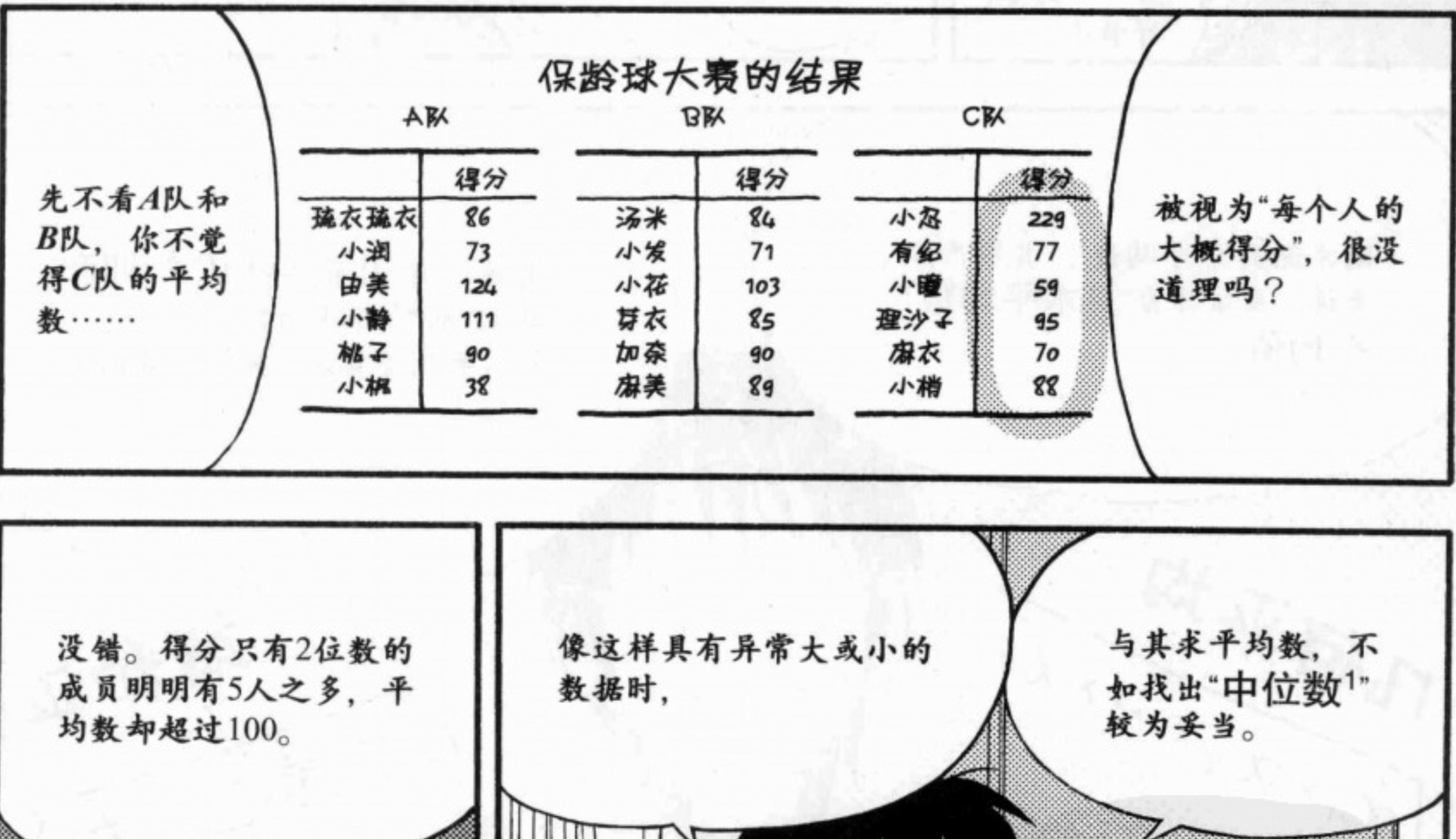
标准差
为什么要有标准差：表现数据的离散程度。
将A B对的得分采用如下图表示出来，可以明显看出来数据的离散程度。
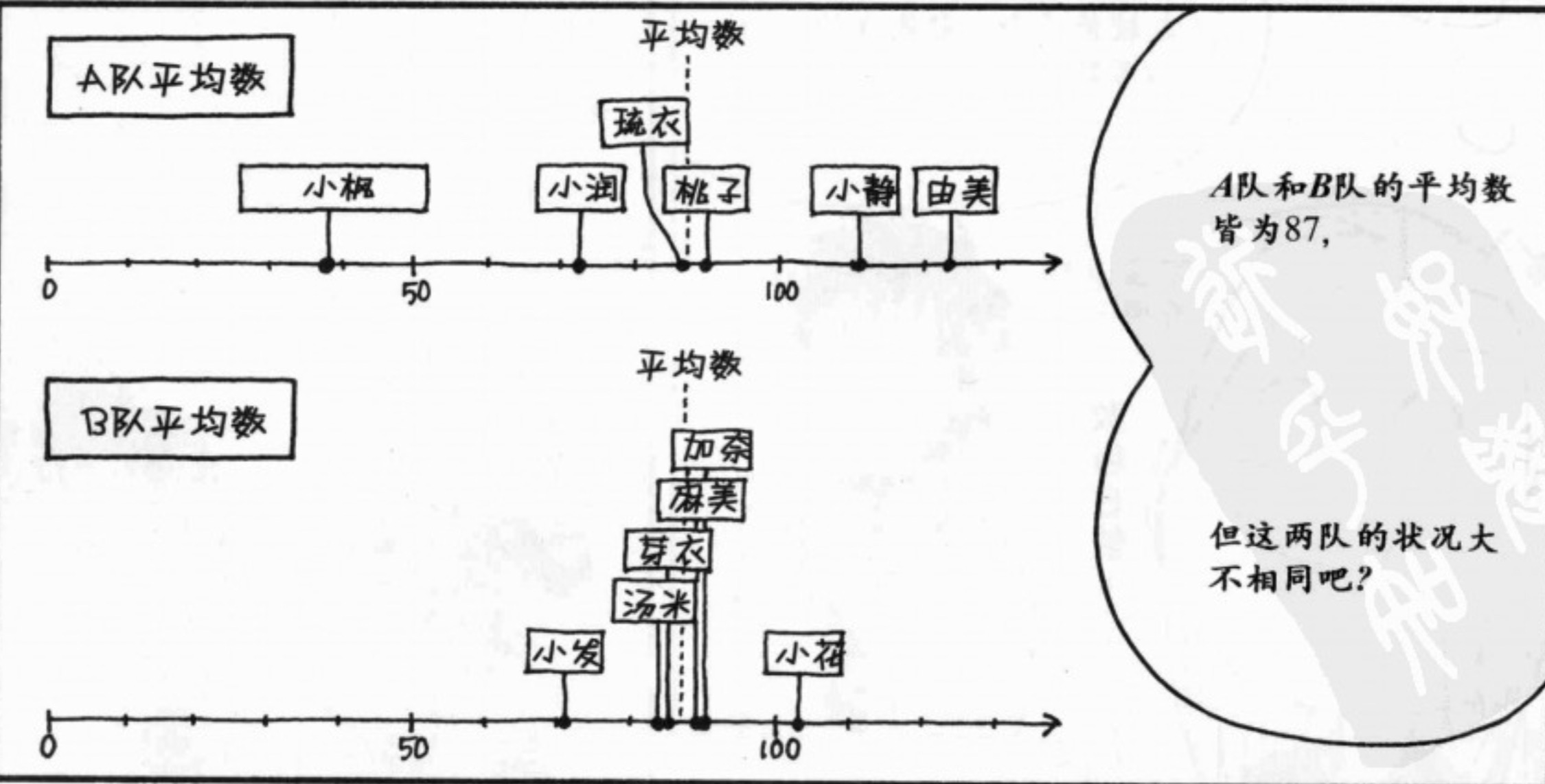
标准差的最小值为0，表示完全不离散，数值越大，表示数据越离散。
小结
三、数据的整体状态（分类数据）
四、标准计分和离差
为什么要标准化
以下是考试成绩表，琉衣和由美的英语和古文分别都考了90分，能说两者的价值相同吗？不能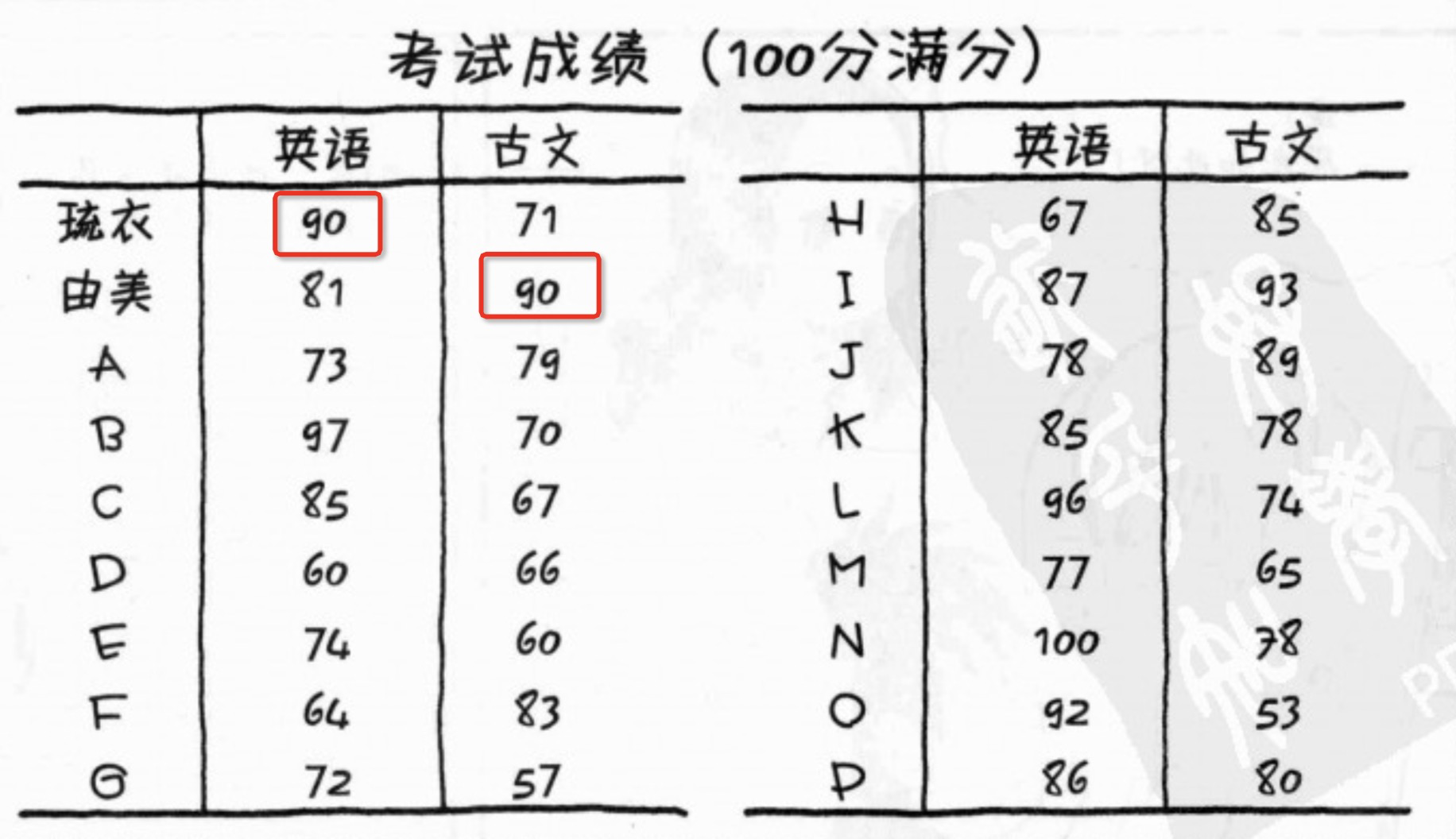
距离均值的距离不同，价值不同。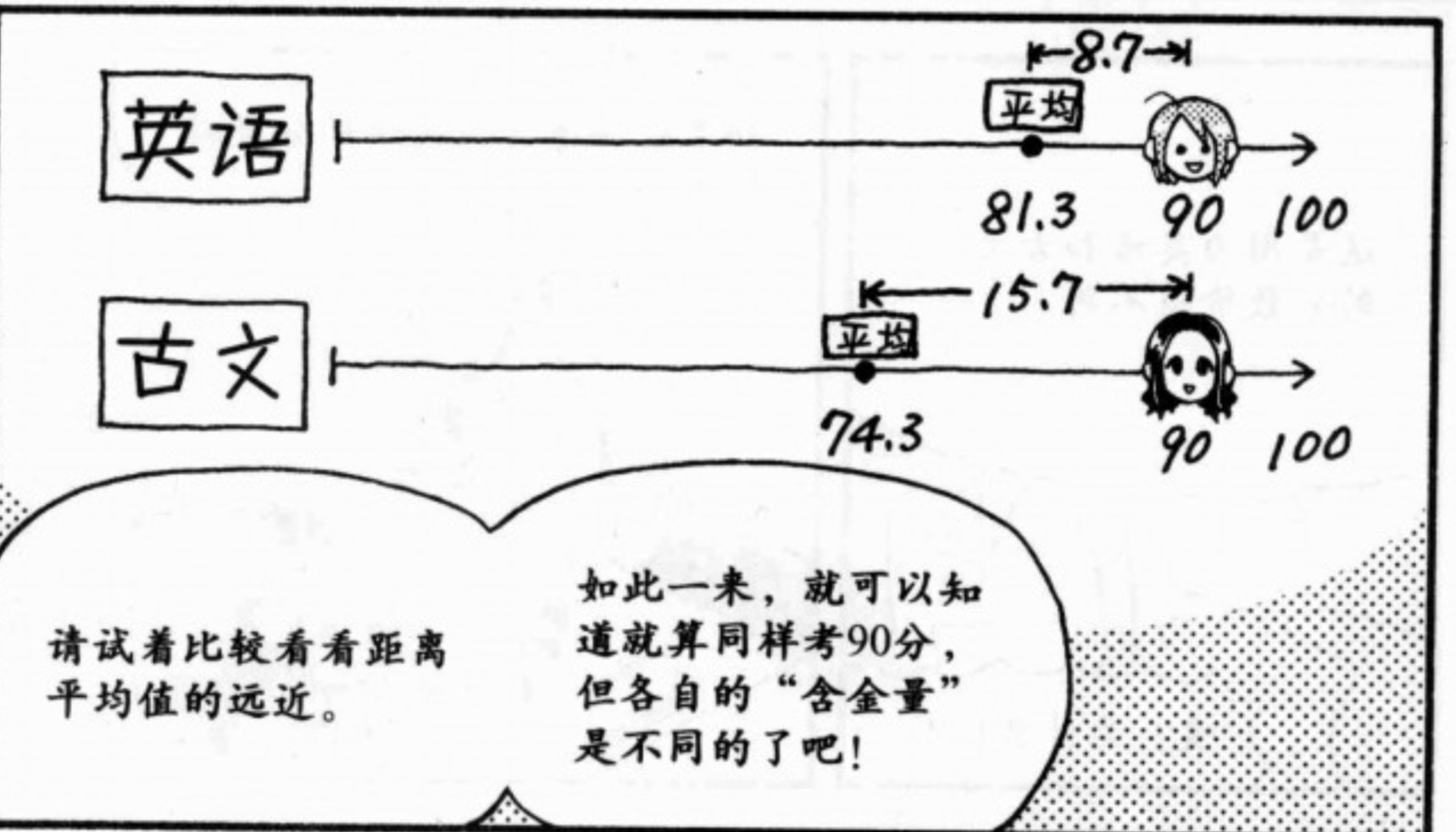
此外，即使距离均值的距离相同，能说价值一样吗？也不能，还得看标准差，看数据的离散程度。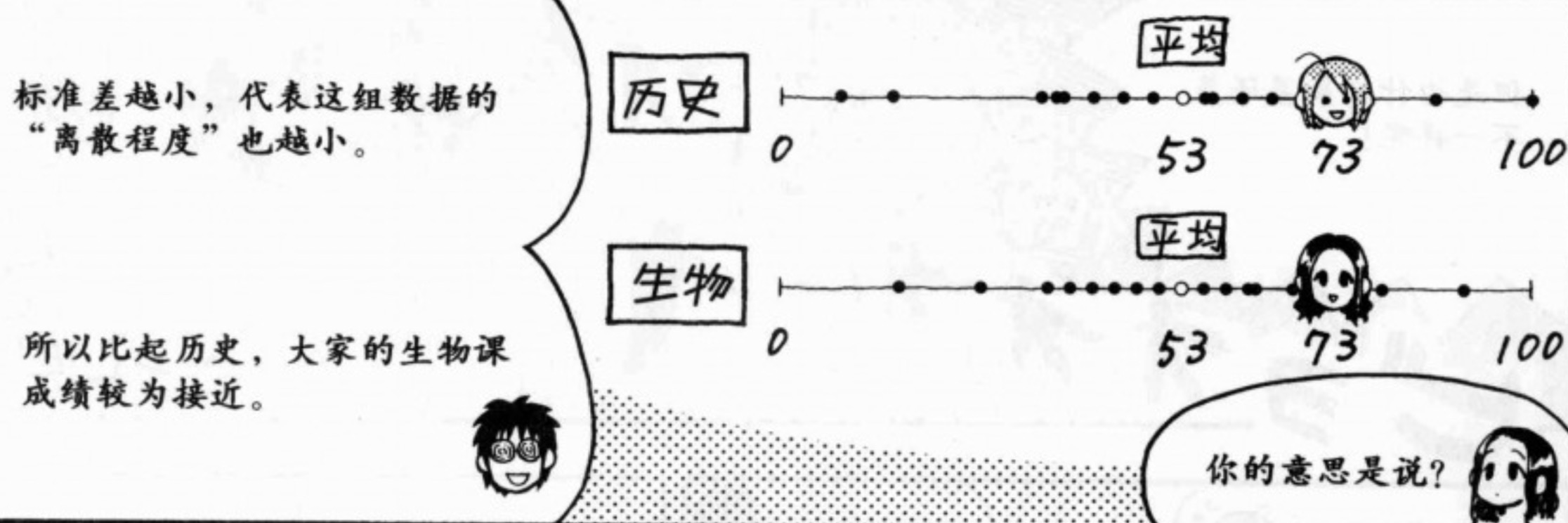
从考试的角度来说，生物的1分就比历史的一分重要。因此即使有1分的差距，也会大大影响排名。
所以，单纯的看原始数据不能表达真实情况，需要标准化，标准化后就好比较了。
如何标准化
以平均值和标准差作为基础计算
标准计分的特征
无论作为变量的满分为几分，其标准计分的平均数势必为0，而其标准差 势必为1.
无论作为变量的单位是什么，其标准计分的平均数势必为0，而其标准差 势必为1.
离差
离差 = 标准计分 * 10 + 50
关于离差的几点解释，没有看懂。
五、几率率
几率密度函数
直方图中，将距离缩小至极限后，所得曲线的公式，就是几率密度函数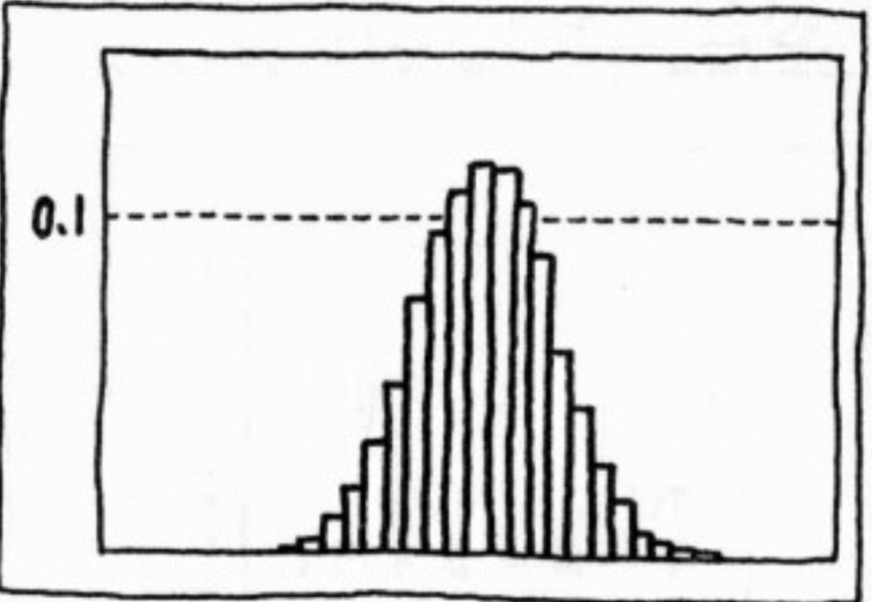
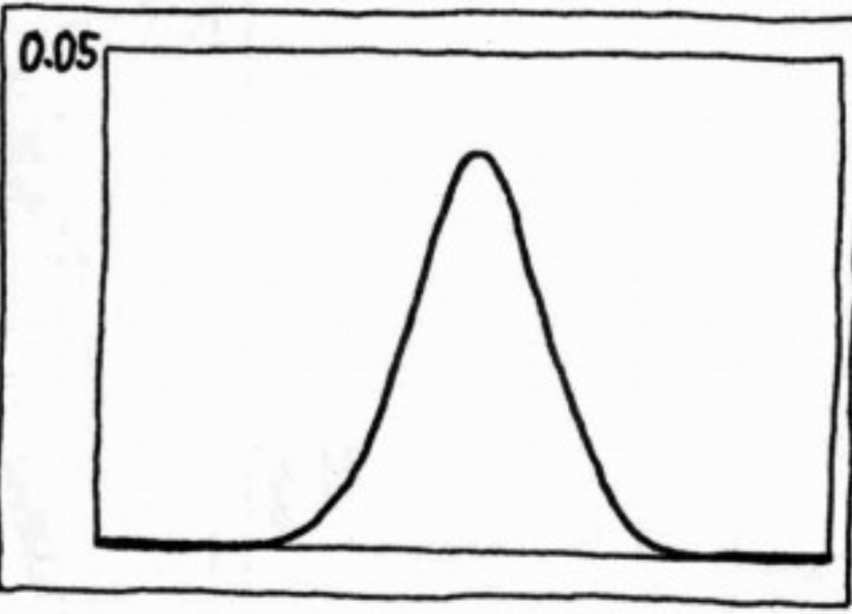
正态分布
特征
- 以平均值为中心呈左右对称分布
- 受到平均值和标准差的影响
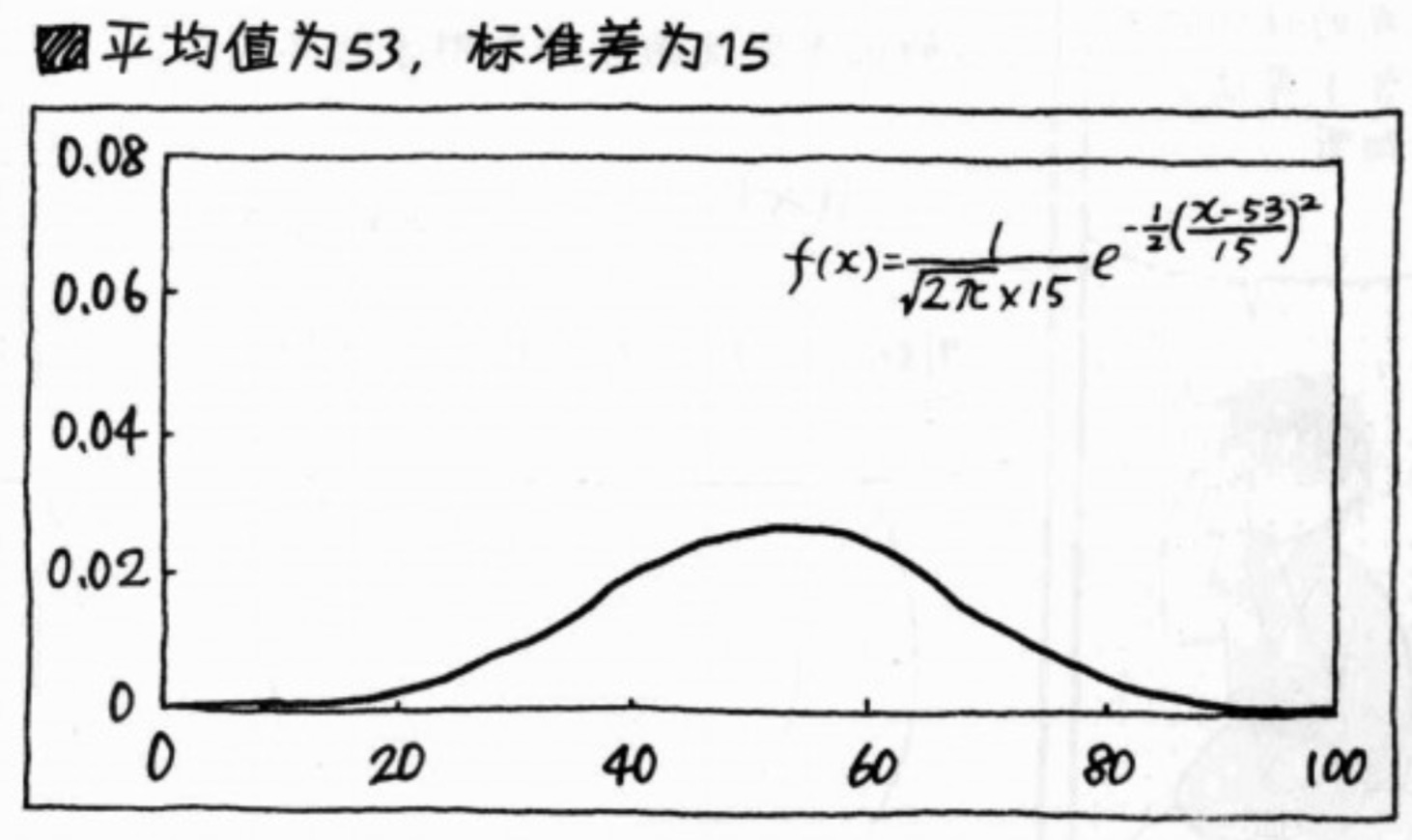
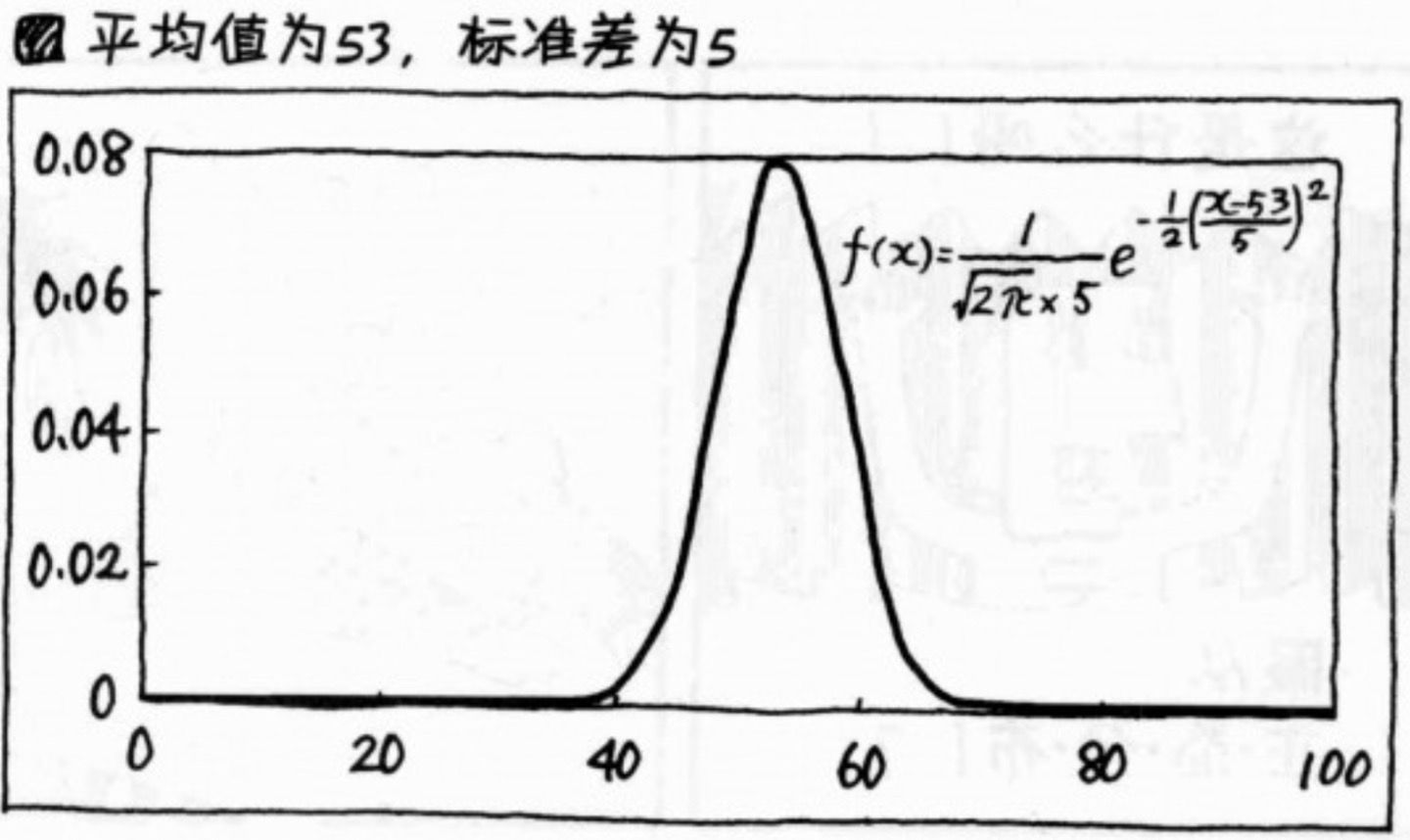
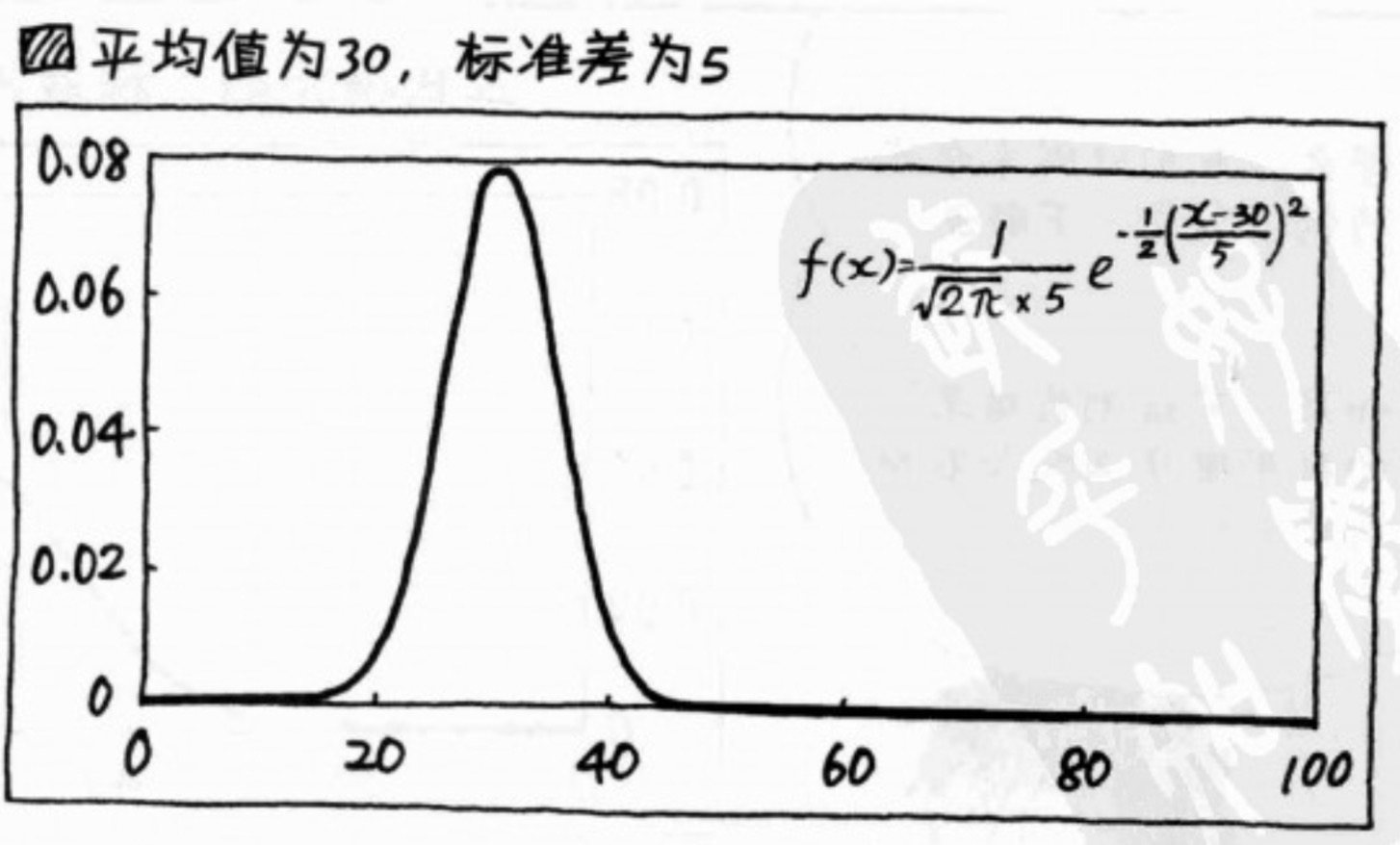
在统计学上，说 服从正态分布，要说“服从 平均值为xx，标准差为xx的正态分布”。正态分布的曲线公式也和均值和标准差强相关
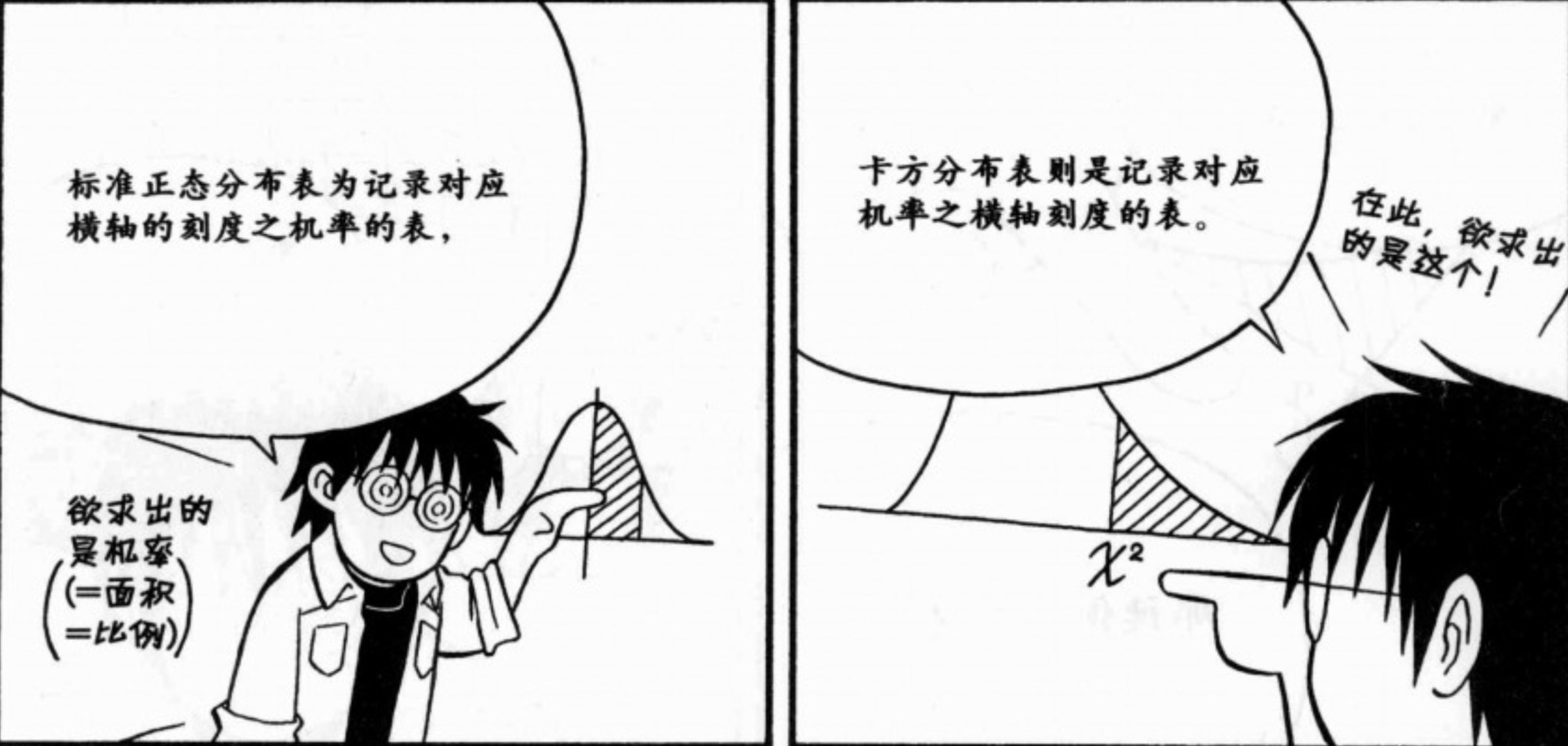
标准正态分布的特征
- 这里已经引入了比率的概念（P值）。整体曲线和x轴围起来的区域面积为1，落在其中的概率也为1。
卡方分布
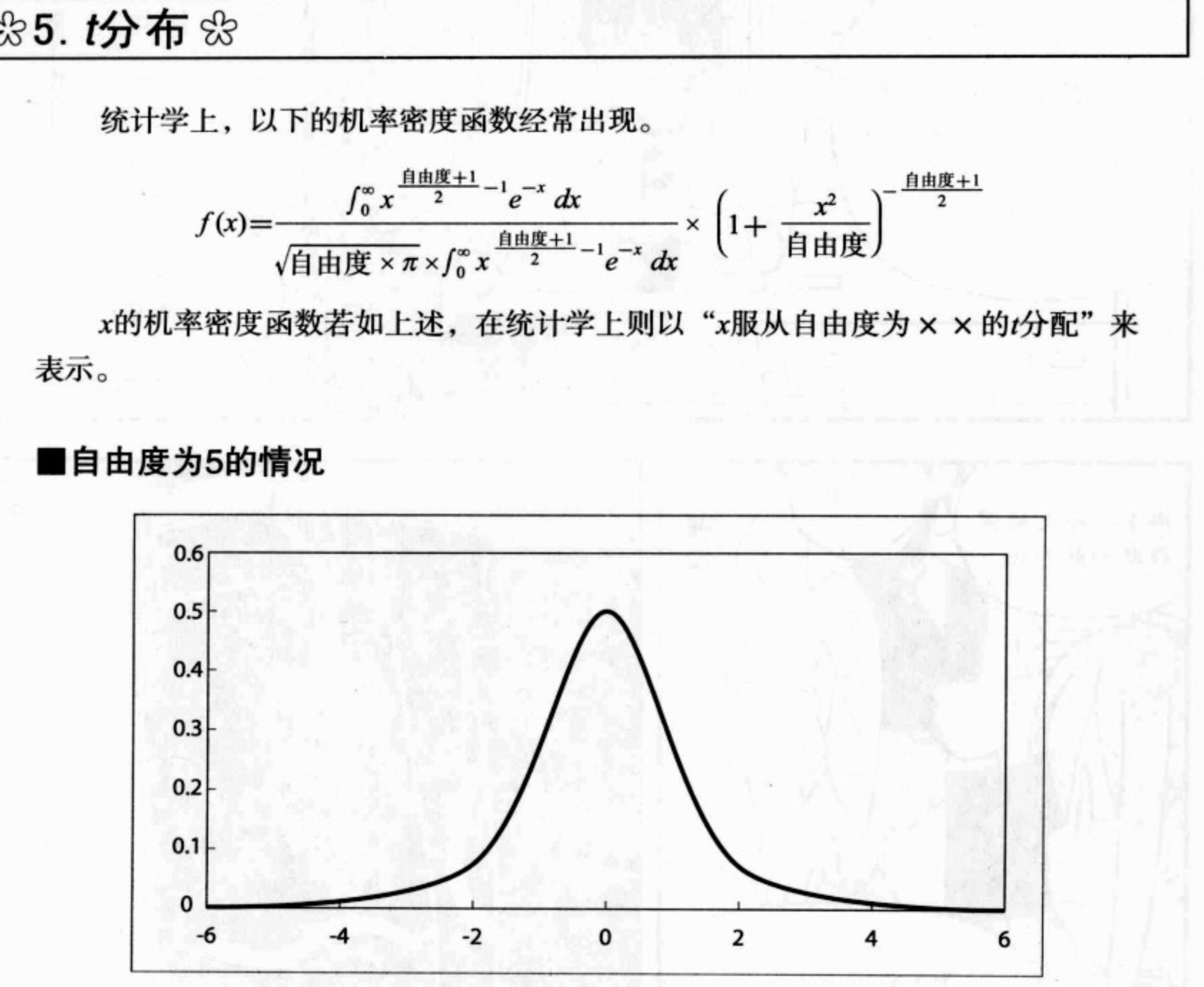
t分布和F分布
小结
六 相关分析
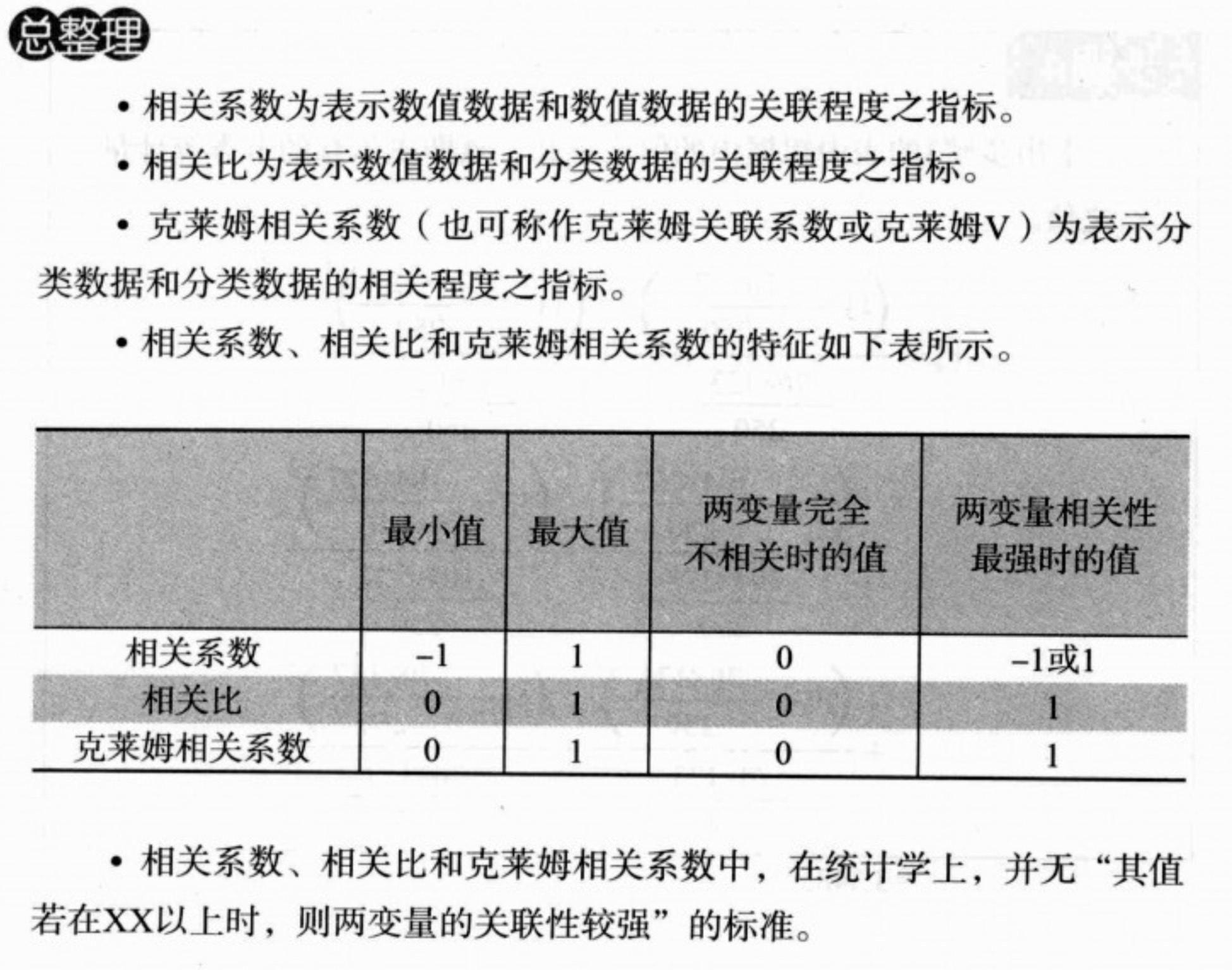
描述不同种类数据之间的相关性的指标
数据种类不同，指标也不同。数值数据和分类数据的含义见第一章。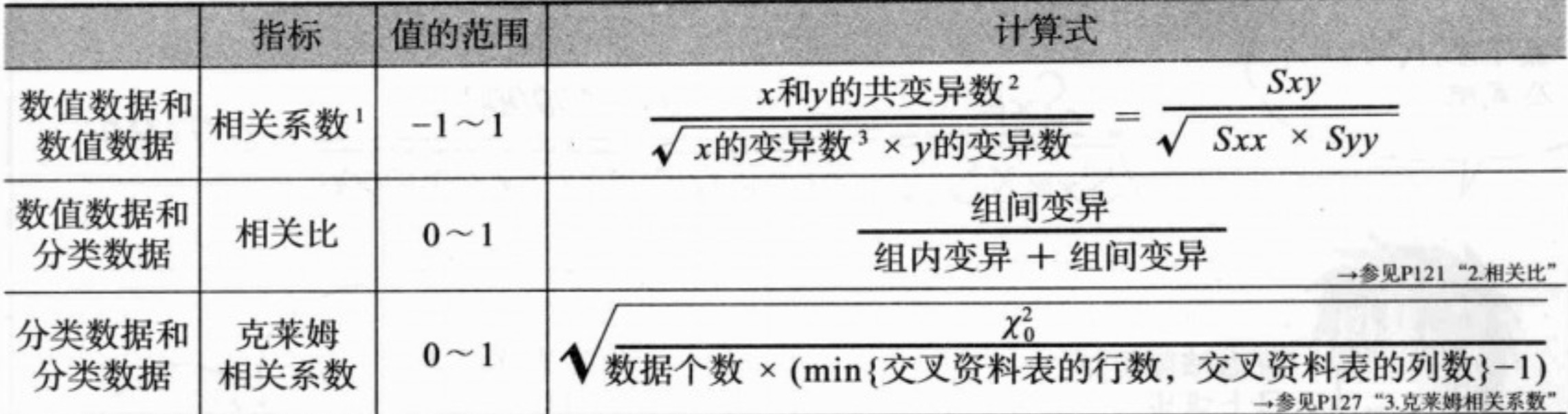
相关系数
正相关、不相关、负相关的形象表示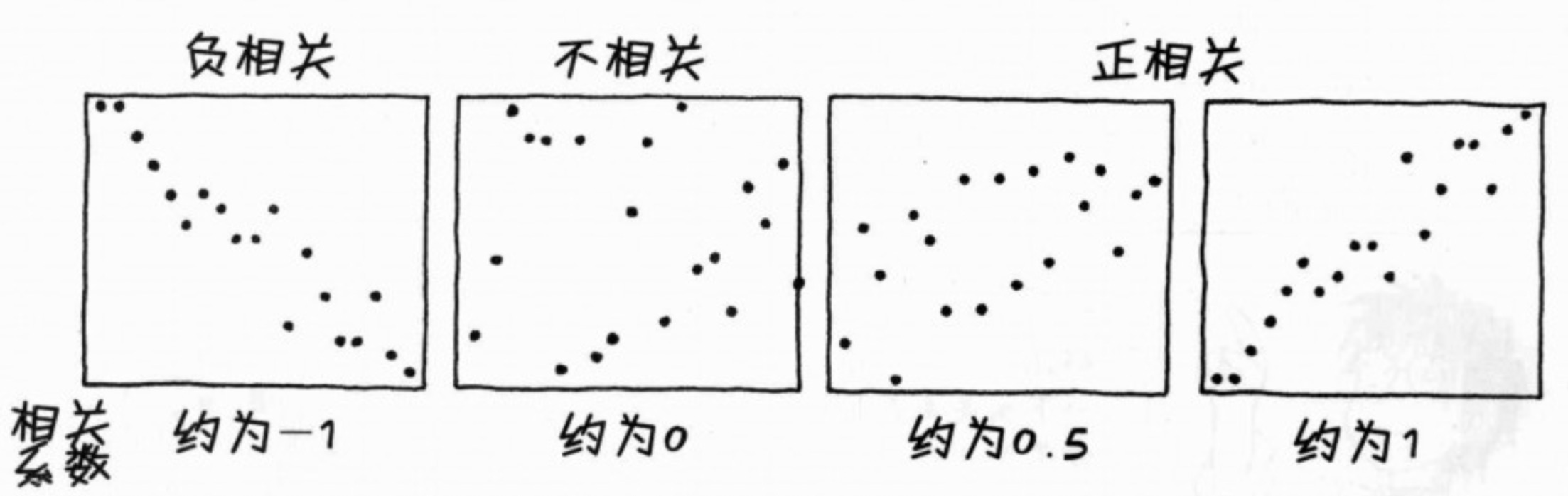
相关系数的绝对值越是趋近于1，代表两变量越相关；越是趋近于0，代表两变量越不相关。
相关比
数值数据和分类数据的相关性采用「相关比」来表示。比如如下调查问卷数据，年龄属于数值数据，品牌属于分类数据。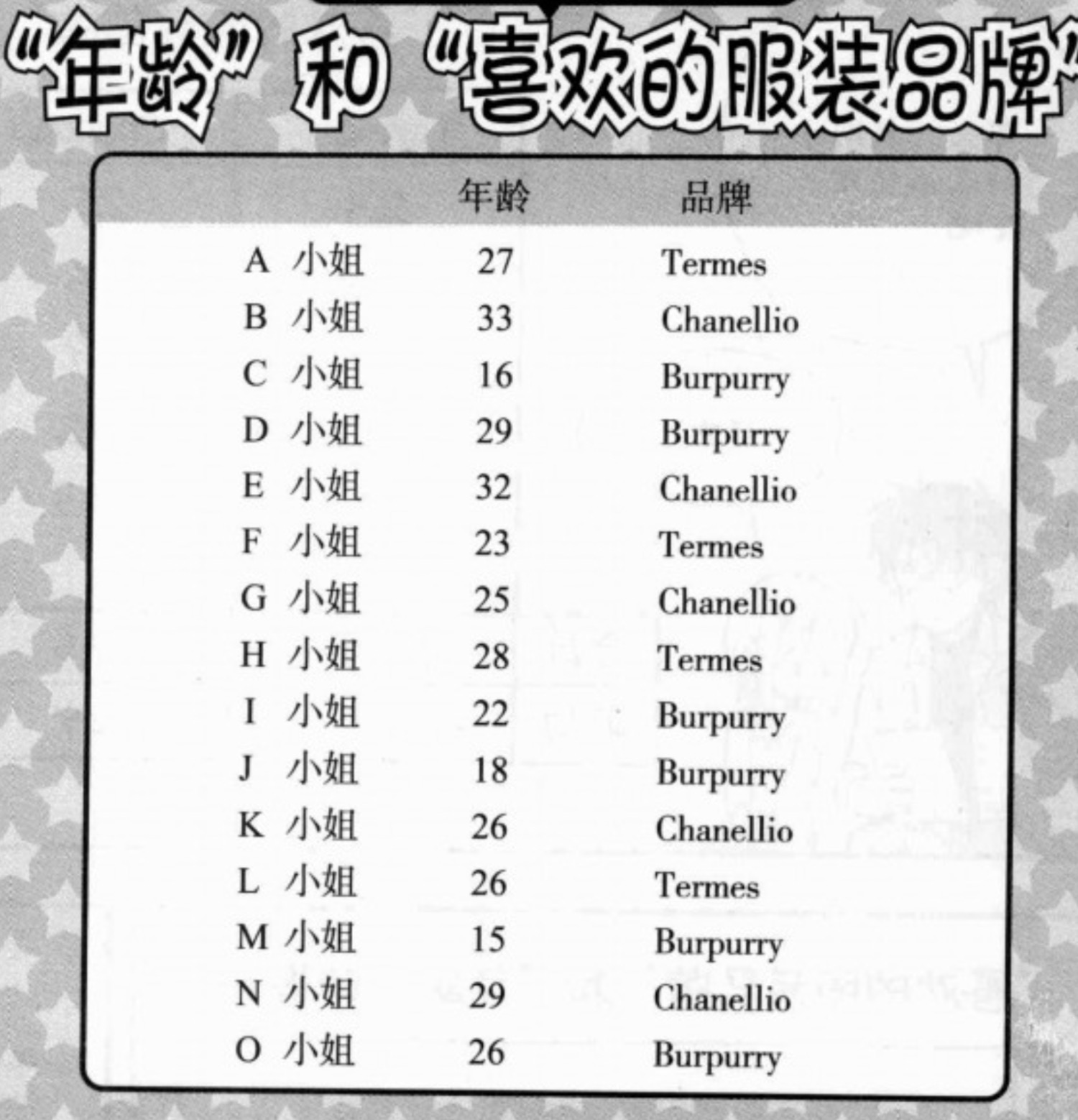
计算方法在此不详述，可参考
相关比的值介于0-1之间。同样，相关性越强，其值越接近于1，反之越接近于0.
克莱姆相关系数
小结
七、检验
何为检验
所谓“检验”是由样本数据来推测分析者针对总体所建立的假说是否正确的分析方法。“检验”的正确名称为统计的假说检验。
检验的分类和实例
独立性检验为推测“总体的克莱姆相关系数的值是否为0”的分析方法。也可说推测“交叉表中两变量是否有关联”的分析
检验统计量
检验统计量是将样本数据转换为1个数值的公式。 其意义在于 确定检验的结论。
具体计算公式为：
置信水平和拒绝域
置信水平就是指下图中阴影部分的几率，一般都设置为0.05或0.01。拒绝域为对应置信水平的范围
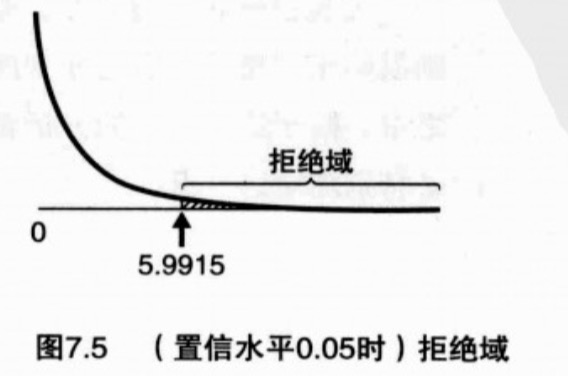
P值
以独立性检验说明，其P值即为：在虚无假说为真的情况下，则本次求出的值为大于或等于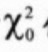
的几率。
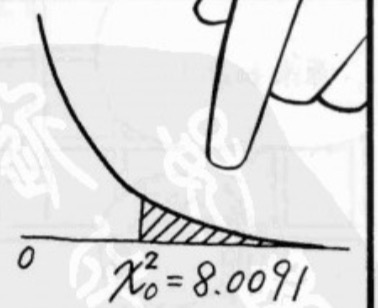
即阴影部分的几率。
这里基于一个结论：若总体的克莱姆相关系数的值为0，则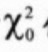遵守卡方分布
为“检验”下结论的根据
- 检验统计量是否在拒绝域中
- P值是否小于置信水平
如何进行“检验”
1、定义总体
2、建立虚无假说和对立假说
3、选择要进行的检验种类
4、决定置信水平
5、从样本数据中求出检验统计量的值
6、调查在步骤5所求出的检验统计量值，是否在拒绝域之中
7、所在步骤6中检测统计量的值在拒绝域之中，则结论为“对立假说成立”。否则结论为“无法判定虚无假说为误”（注意：不能说 虚无假说正确）
6P、调查在步骤5所求出的检验统计量值对应的P值，是否比置信水平小
7P、步骤6P所得的P值弱小于置信水平，则可作出“对立假说成立”，否则结论为“无法判定虚无假说为误”
其他
问题
- 相关分析和回归分析的区别？
以上记录还比较粗略，可能还比较难理解。后续再通过更加形象化的方式表达出来。
若有收获，就点个赞吧
0 人点赞
