在本教程中,您将学习什么是 rabin-karp 算法。 此外,您还将在 C,C++ ,Java 和 Python 中找到 rabin-karp 算法的工作示例。
Rabin-Karp 算法是一种用于使用哈希函数搜索/匹配文本中的模式的算法。 与朴素的字符串匹配算法不同,它在初始阶段不会遍历每个字符,而是过滤不匹配的字符,然后执行比较。
哈希函数是一种将较大的输入值映射到较小的输出值的工具。 此输出值称为哈希值。
Rabin-Karp 算法如何工作?
采取一系列字符并检查是否存在所需字符串。 如果找到了可能性,则执行字符匹配。
让我们通过以下步骤来了解算法:
假设文本为:

文本
,并且要在上述文本中搜索的字符串为:
模式让我们为问题中要使用的字符分配一个数值(
v)/权重。 在这里,我们仅采用了前十个字母(即 A 到 J)。
文本权重m是模式的长度,n是文本的长度。 在此,m = 10 and n = 3.
令d为输入集中的字符数。 在这里,我们采用了输入集{A, B, C, ..., J}。 因此,d = 10。 您可以为d假定任何合适的值。让我们计算模式的哈希值。

文本的哈希值
hash value for pattern(p) = Σ(v * dm-1) mod 13= ((3 * 102) + (4 * 101) + (4 * 100)) mod 13= 344 mod 13= 6
在上面的计算中,选择质数(此处为 13),以便我们可以使用单精度算术执行所有计算。
- 计算大小为
m的文本窗口的哈希值。
For the first window ABC,hash value for text(t) = Σ(v * dn-1) mod 13= ((1 * 102) + (2 * 101) + (3 * 100)) mod 13= 123 mod 13= 6
- 将模式的哈希值与文本的哈希值进行比较。 如果它们匹配,则执行字符匹配。
在上面的示例中,第一个窗口的哈希值(即t)与p匹配,因此请在ABC和CDD之间进行字符匹配。 由于它们不匹配,请转到下一个窗口。 - 我们通过减去第一项并添加下一项来计算下一个窗口的哈希值,如下所示。
t = ((1 * 102) + ((2 * 101) + (3 * 100)) * 10 + (3 * 100)) mod 13= 233 mod 13= 12
为了优化此过程,我们以以下方式使用先前的哈希值。
t = ((d * (t - v[character to be removed] * h) + v[character to be added] ) mod 13= ((10 * (6 - 1 * 9) + 3 )mod 13= 12Where, h = dm-1 = 103-1 = 100.
- 对于
BCC,t = 12(≠ 6)。 因此,转到下一个窗口。
经过几次搜索,我们将在文本中获得窗口CDA的匹配项。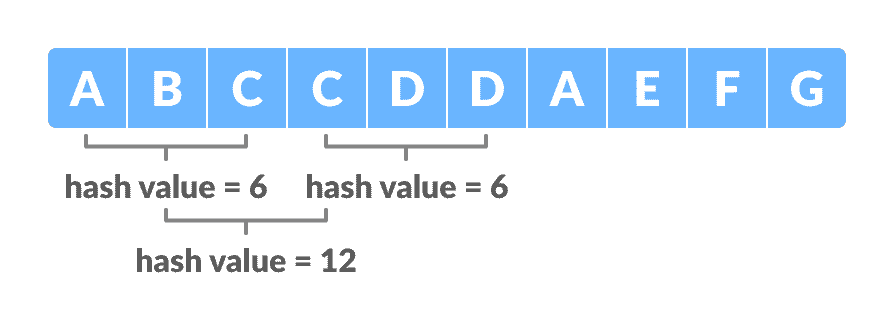
不同窗口的哈希值
算法
n = t.length
m = p.length
h = dm-1 mod q
p = 0
t0 = 0
for i = 1 to m
p = (dp + p[i]) mod q
t0 = (dt0 + t[i]) mod q
for s = 0 to n - m
if p = ts
if p[1.....m] = t[s + 1..... s + m]
print "pattern found at position" s
If s < n-m
ts + 1 = (d (ts - t[s + 1]h) + t[s + m + 1]) mod q
Python,Java 和 C/C++ 示例
# Rabin-Karp algorithm in python
d = 10
def search(pattern, text, q):
m = len(pattern)
n = len(text)
p = 0
t = 0
h = 1
i = 0
j = 0
for i in range(m-1):
h = (h*d) % q
# Calculate hash value for pattern and text
for i in range(m):
p = (d*p + ord(pattern[i])) % q
t = (d*t + ord(text[i])) % q
# Find the match
for i in range(n-m+1):
if p == t:
for j in range(m):
if text[i+j] != pattern[j]:
break
j += 1
if j == m:
print("Pattern is found at position: " + str(i+1))
if i < n-m:
t = (d*(t-ord(text[i])*h) + ord(text[i+m])) % q
if t < 0:
t = t+q
text = "ABCCDDAEFG"
pattern = "CDD"
q = 13
search(pattern, text, q)
// Rabin-Karp algorithm in Java
public class RabinKarp {
public final static int d = 10;
static void search(String pattern, String txt, int q) {
int m = pattern.length();
int n = txt.length();
int i, j;
int p = 0;
int t = 0;
int h = 1;
for (i = 0; i < m - 1; i++)
h = (h * d) % q;
// Calculate hash value for pattern and text
for (i = 0; i < m; i++) {
p = (d * p + pattern.charAt(i)) % q;
t = (d * t + txt.charAt(i)) % q;
}
// Find the match
for (i = 0; i <= n - m; i++) {
if (p == t) {
for (j = 0; j < m; j++) {
if (txt.charAt(i + j) != pattern.charAt(j))
break;
}
if (j == m)
System.out.println("Pattern is found at position: " + (i + 1));
}
if (i < n - m) {
t = (d * (t - txt.charAt(i) * h) + txt.charAt(i + m)) % q;
if (t < 0)
t = (t + q);
}
}
}
public static void main(String[] args) {
String txt = "ABCCDDAEFG";
String pattern = "CDD";
int q = 13;
search(pattern, txt, q);
}
}
// Rabin-Karp algorithm in C
#include <stdio.h>
#include <string.h>
#define d 10
void rabinKarp(char pattern[], char text[], int q) {
int m = strlen(pattern);
int n = strlen(text);
int i, j;
int p = 0;
int t = 0;
int h = 1;
for (i = 0; i < m - 1; i++)
h = (h * d) % q;
// Calculate hash value for pattern and text
for (i = 0; i < m; i++) {
p = (d * p + pattern[i]) % q;
t = (d * t + text[i]) % q;
}
// Find the match
for (i = 0; i <= n - m; i++) {
if (p == t) {
for (j = 0; j < m; j++) {
if (text[i + j] != pattern[j])
break;
}
if (j == m)
printf("Pattern is found at position: %d \n", i + 1);
}
if (i < n - m) {
t = (d * (t - text[i] * h) + text[i + m]) % q;
if (t < 0)
t = (t + q);
}
}
}
int main() {
char text[] = "ABCCDDAEFG";
char pattern[] = "CDD";
int q = 13;
rabinKarp(pattern, text, q);
}
// Rabin-Karp algorithm in C++
#include <string.h>
#include <iostream>
using namespace std;
#define d 10
void rabinKarp(char pattern[], char text[], int q) {
int m = strlen(pattern);
int n = strlen(text);
int i, j;
int p = 0;
int t = 0;
int h = 1;
for (i = 0; i < m - 1; i++)
h = (h * d) % q;
// Calculate hash value for pattern and text
for (i = 0; i < m; i++) {
p = (d * p + pattern[i]) % q;
t = (d * t + text[i]) % q;
}
// Find the match
for (i = 0; i <= n - m; i++) {
if (p == t) {
for (j = 0; j < m; j++) {
if (text[i + j] != pattern[j])
break;
}
if (j == m)
cout << "Pattern is found at position: " << i + 1 << endl;
}
if (i < n - m) {
t = (d * (t - text[i] * h) + text[i + m]) % q;
if (t < 0)
t = (t + q);
}
}
}
int main() {
char text[] = "ABCCDDAEFG";
char pattern[] = "CDD";
int q = 13;
rabinKarp(pattern, text, q);
}
Rabin-Karp 算法的局限性
虚假命中
当模式的哈希值与文本窗口的哈希值匹配,但该窗口不是实际的模式时,则称为虚假命中。
杂散命中会增加算法的时间复杂度。 为了最小化杂散命中,我们使用模数。 它大大减少了伪造的打击。
Rabin-Karp 算法复杂度
Rabin-Karp 算法的平均情况和最佳情况复杂度为O(m + n),最坏情况下的复杂度为O(mn)。
当所有窗口出现虚假命中数时,最坏情况下的复杂度就会发生。
Rabin-Karp 算法应用
- 用于模式匹配
- 用于在较大的文本中搜索字符串

