在本教程中,您将学习选择排序的工作方式。 此外,您还将找到使用 C,C++ ,Java 和 Python 进行选择排序的工作示例。
选择排序是一种算法,它在每次迭代中从未排序列表中选择最小的元素,并将该元素放在未排序列表的开头。
选择排序如何工作?
将第一个元素设置为
minimum。
选择第一个元素作为最小值将
minimum与第二个元素进行比较。 如果第二个元素小于minimum,则将第二个元素指定为minimum。
将minimum与第三个元素进行比较。 同样,如果第三个元素较小,则将minimum分配给第三个元素,否则不执行任何操作。 该过程一直进行到最后一个元素。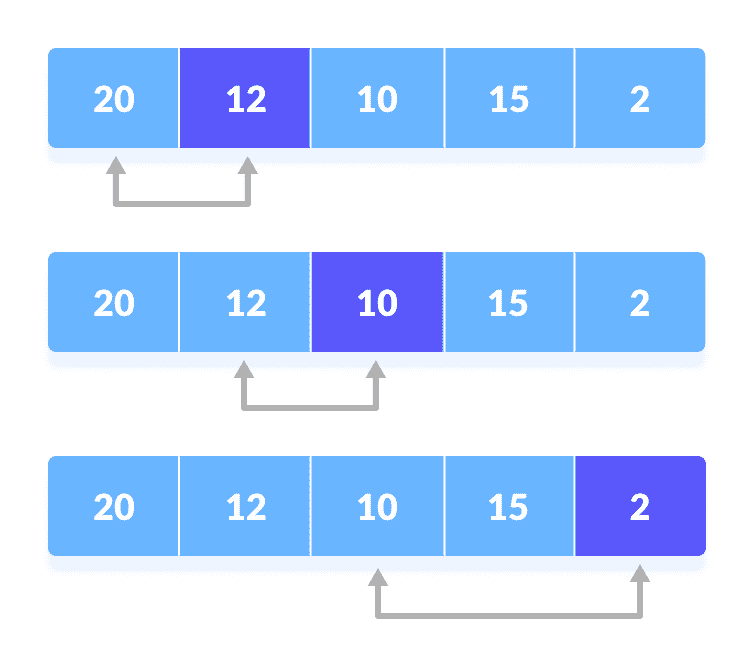
将其余元素的最小值进行比较每次迭代后,
minimum都放在未排序列表的前面。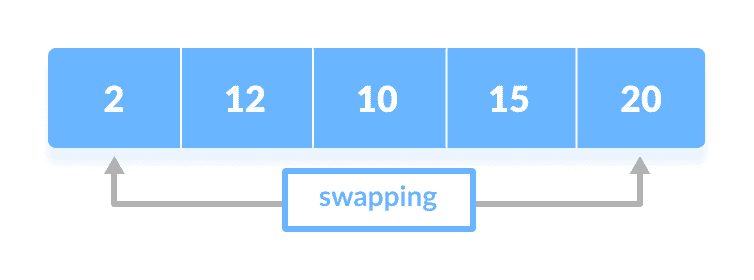
以最少的
交换第一个对于每次迭代,索引从第一个未排序元素开始。 重复步骤 1 到 3,直到所有元素都放置在正确的位置。
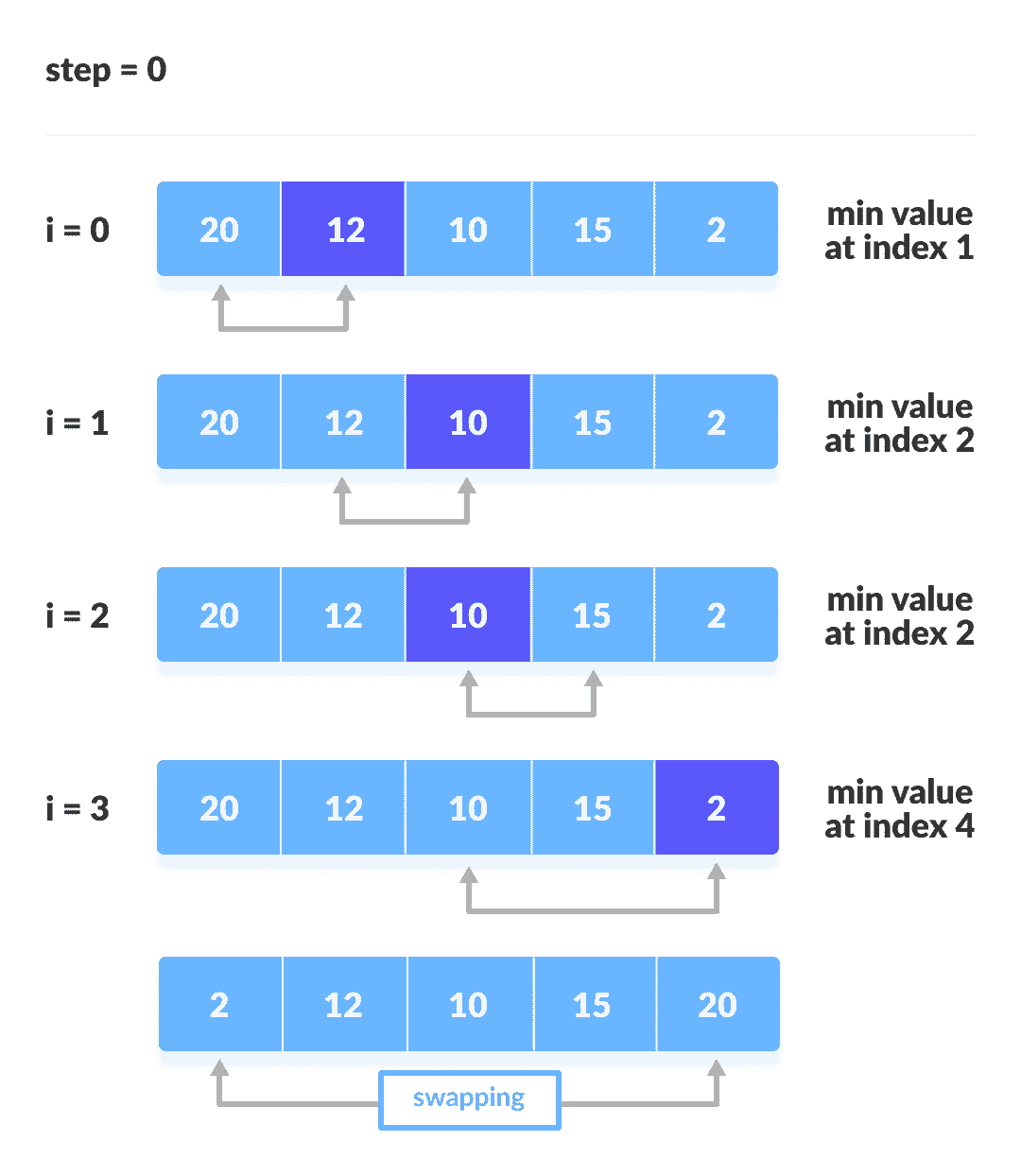
第一次迭代
第二次迭代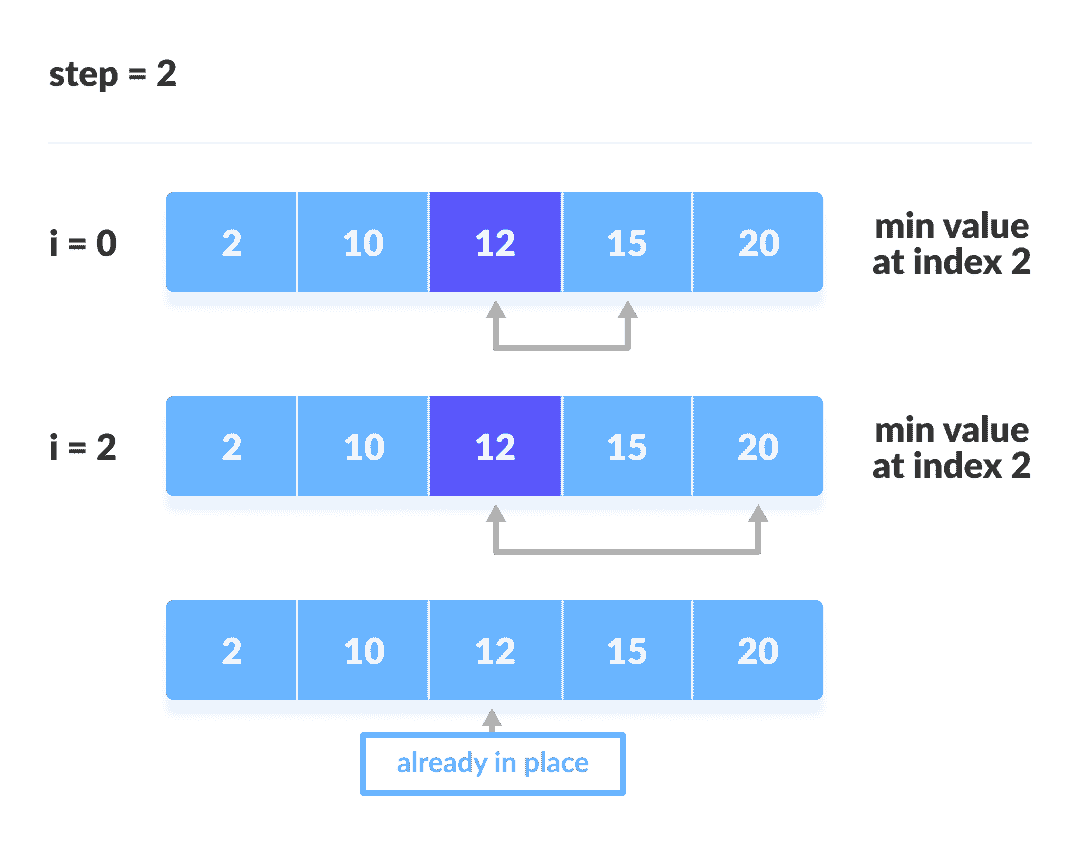
第三次迭代
[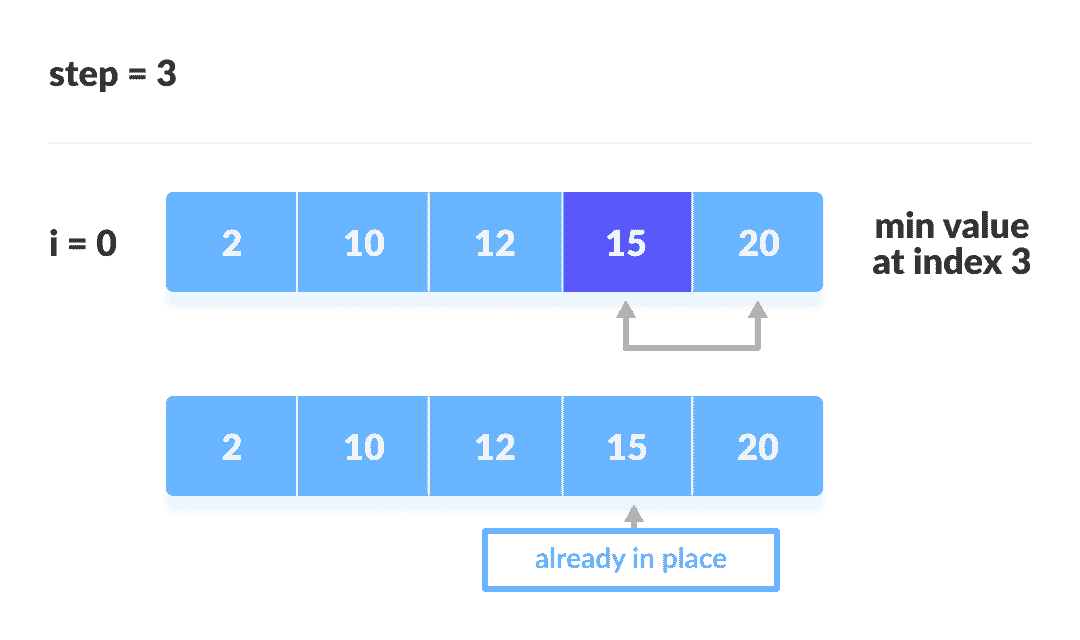
第四次迭代
选择排序算法
selectionSort(array, size)repeat (size - 1) timesset the first unsorted element as the minimumfor each of the unsorted elementsif element < currentMinimumset element as new minimumswap minimum with first unsorted positionend selectionSort
Python,Java 和 C/C++ 示例
# Selection sort in Python
def selectionSort(array, size):
for step in range(size):
min_idx = step
for i in range(step + 1, size):
# to sort in descending order, change > to < in this line
# select the minimum element in each loop
if array[i] < array[min_idx]:
min_idx = i
# put min at the correct position
(array[step], array[min_idx]) = (array[min_idx], array[step])
data = [-2, 45, 0, 11, -9]
size = len(data)
selectionSort(data, size)
print('Sorted Array in Ascending Order:')
print(data)
// Selection sort in Java
import java.util.Arrays;
class SelectionSort {
void selectionSort(int array[]) {
int size = array.length;
for (int step = 0; step < size - 1; step++) {
int min_idx = step;
for (int i = step + 1; i < size; i++) {
// To sort in descending order, change > to < in this line.
// Select the minimum element in each loop.
if (array[i] < array[min_idx]) {
min_idx = i;
}
}
// put min at the correct position
int temp = array[step];
array[step] = array[min_idx];
array[min_idx] = temp;
}
}
// driver code
public static void main(String args[]) {
int[] data = { 20, 12, 10, 15, 2 };
SelectionSort ss = new SelectionSort();
ss.selectionSort(data);
System.out.println("Sorted Array in Ascending Order: ");
System.out.println(Arrays.toString(data));
}
}
// Selection sort in C
#include <stdio.h>
// function to swap the the position of two elements
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
void selectionSort(int array[], int size) {
for (int step = 0; step < size - 1; step++) {
int min_idx = step;
for (int i = step + 1; i < size; i++) {
// To sort in descending order, change > to < in this line.
// Select the minimum element in each loop.
if (array[i] < array[min_idx])
min_idx = i;
}
// put min at the correct position
swap(&array[min_idx], &array[step]);
}
}
// function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; ++i) {
printf("%d ", array[i]);
}
printf("\n");
}
// driver code
int main() {
int data[] = {20, 12, 10, 15, 2};
int size = sizeof(data) / sizeof(data[0]);
selectionSort(data, size);
printf("Sorted array in Acsending Order:\n");
printArray(data, size);
}
// Selection sort in C++
#include <iostream>
using namespace std;
// function to swap the the position of two elements
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
// function to print an array
void printArray(int array[], int size) {
for (int i = 0; i < size; i++) {
cout << array[i] << " ";
}
cout << endl;
}
void selectionSort(int array[], int size) {
for (int step = 0; step < size - 1; step++) {
int min_idx = step;
for (int i = step + 1; i < size; i++) {
// To sort in descending order, change > to < in this line.
// Select the minimum element in each loop.
if (array[i] < array[min_idx])
min_idx = i;
}
// put min at the correct position
swap(&array[min_idx], &array[step]);
}
}
// driver code
int main() {
int data[] = {20, 12, 10, 15, 2};
int size = sizeof(data) / sizeof(data[0]);
selectionSort(data, size);
cout << "Sorted array in Acsending Order:\n";
printArray(data, size);
}
复杂度
| 周期 | 比较次数 |
|---|---|
| 第一 | (n-1) |
| 第二 | (n-2) |
| 第三 | (n-3) |
| … | … |
| 最后 | 1 |
比较次数:(n - 1) + (n - 2) + (n - 3) + ..... + 1 = n(n - 1) / 2几乎等于n^2。
复杂度 = O(n^2)
同样,我们可以通过简单地观察循环数来分析复杂度。 有 2 个循环,因此复杂度为n*n = n^2。
时间复杂度:
- 最坏情况的复杂度:
O(n^2)
如果我们要以升序排序,而数组是以降序排序,那么会发生最坏情况。 - 最佳情况复杂度:
O(n^2)
在对数组进行排序时会发生 - 平均情况复杂度:
O(n^2)
当数组的元素处于混乱顺序(既不升也不降)时,会发生这种情况。
选择排序的时间复杂度在所有情况下都是相同的。 在每一步中,您都必须找到最小的元素并将其放在正确的位置。 直到没有到达数组的末尾,才知道最小元素。
空间复杂度:
空间复杂度为O(1),因为使用了额外的变量temp。
选择排序应用
在以下情况下使用选择排序:
- 要排序的一个小列表
- 交换成本无所谓
- 必须对所有要素进行检查
- 写入存储器的成本就像闪存一样重要(与冒泡排序的
O(n^2)相比,写入/交换的次数为O(n))

