生成树和最小生成树

原文： https://www.programiz.com/dsa/spanning-tree-and-minimum-spanning-tree

在本教程中，您将通过示例和图形学习有关生成树和最小生成树的信息。

在学习生成树之前，我们需要了解两个图：无向图和连接图。

无向图是其中边没有指向任何方向的图（即，边是双向的）。

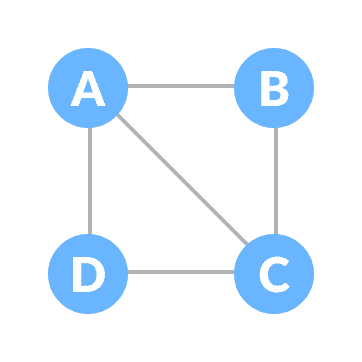
无向图

连通图是其中始终存在从顶点到任何其他顶点的路径的图。

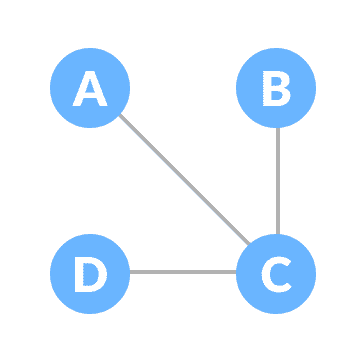
连通图

生成树

生成树是无向图和连通图的子图，其中包括图的所有顶点，这些顶点的边数最少。 如果缺少顶点，则它不是生成树。

边可以分配权重，也可以不分配权重。

可以从完整图形创建的具有n顶点的生成树总数等于n^(n-2)。

如果我们有n = 4，则最大可能的生成树数等于4^(4-2) = 16。 因此，可以从具有 4 个顶点的完整图形中形成 16 个生成树。

生成树的示例

让我们通过以下示例了解生成树：

让原始图为：

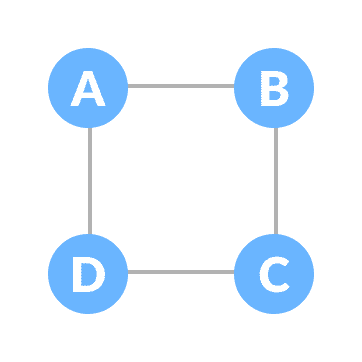
普通的图

可以从上图创建的一些可能的生成树是：

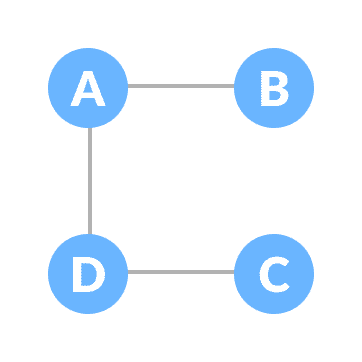
一棵生成树

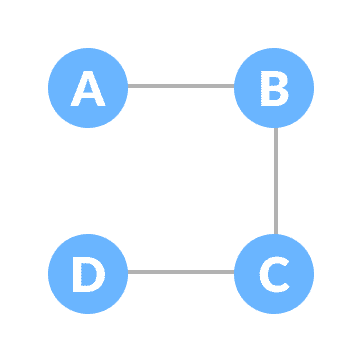
一棵生成树

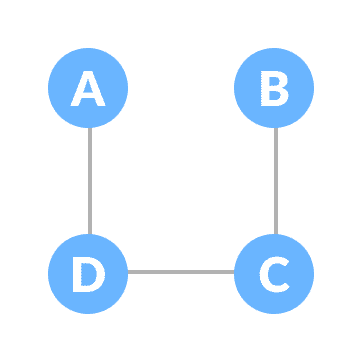
一棵生成树

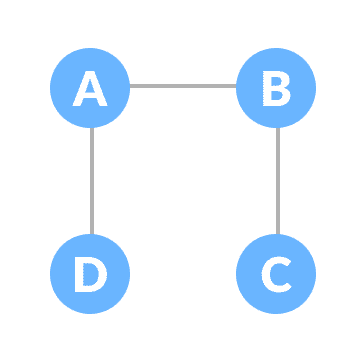
一棵生成树

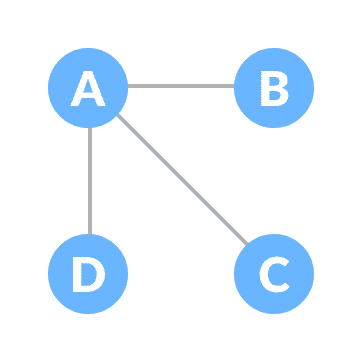
一棵生成树

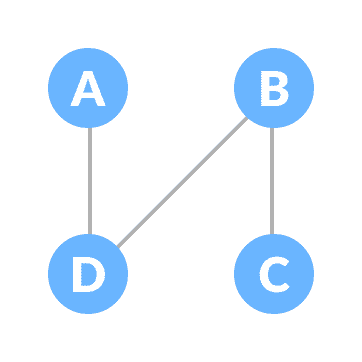
一棵生成树

最小生成树

最小生成树是其中边的权重之和尽可能最小的生成树。

生成树的示例

让我们借助下面的示例了解上面的定义。

初始图形为：

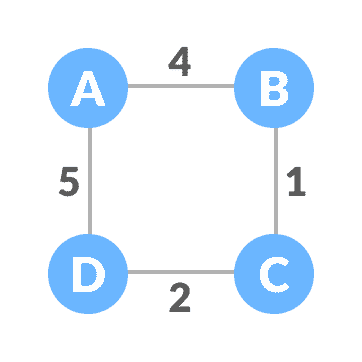
带权图

上图可能的生成树是：

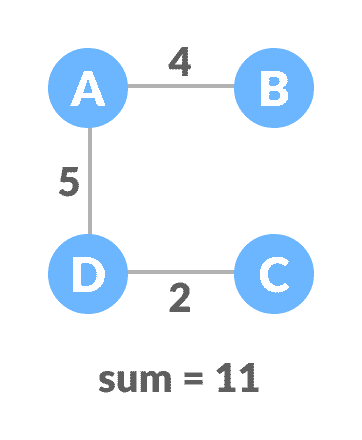
最小生成树 - 1

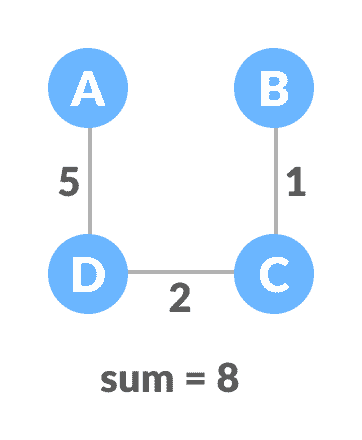
最小生成树- 2

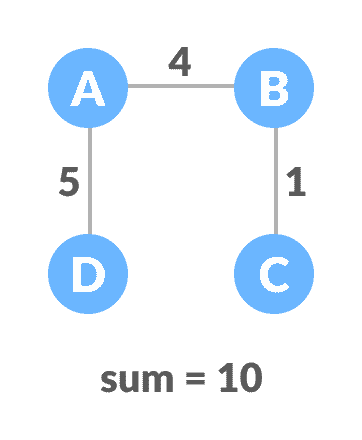
最小生成树 - 3

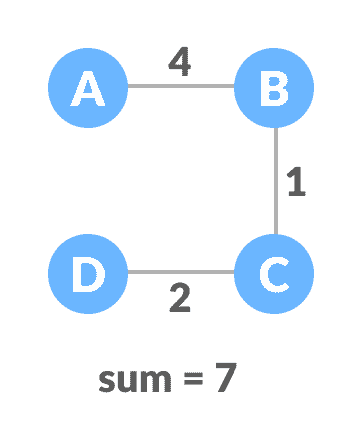
最小生成树 - 4

上述生成树中的最小生成树为：

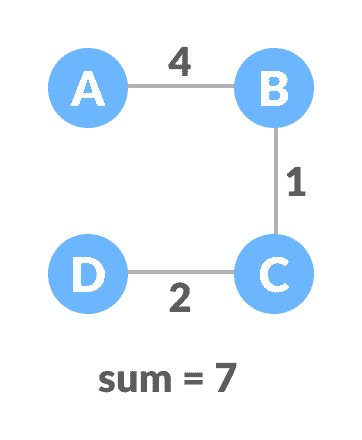
最小生成树

使用以下算法可找到图中的最小生成树：

1. Prim 的算法
2. Kruskal 算法

生成树应用

• 计算机网络路由协议
• 聚类分析
• 民用网络规划

最小生成树应用

• 在地图中查找路径
• 设计诸如电信网络，供水网络和电网的网络。