Dijkstra 算法

原文： https://www.programiz.com/dsa/dijkstra-algorithm

Dijkstra 算法使我们能够找到图形中任意两个顶点之间的最短路径。

它与最小生成树不同，因为两个顶点之间的最短距离可能不包括图形的所有顶点。

Dijkstra 算法的工作原理

Dijkstra 算法的工作原理是，顶点A和D之间的最短路径A -> D的任何子路径B -> D也是顶点B和D之间的最短路径。

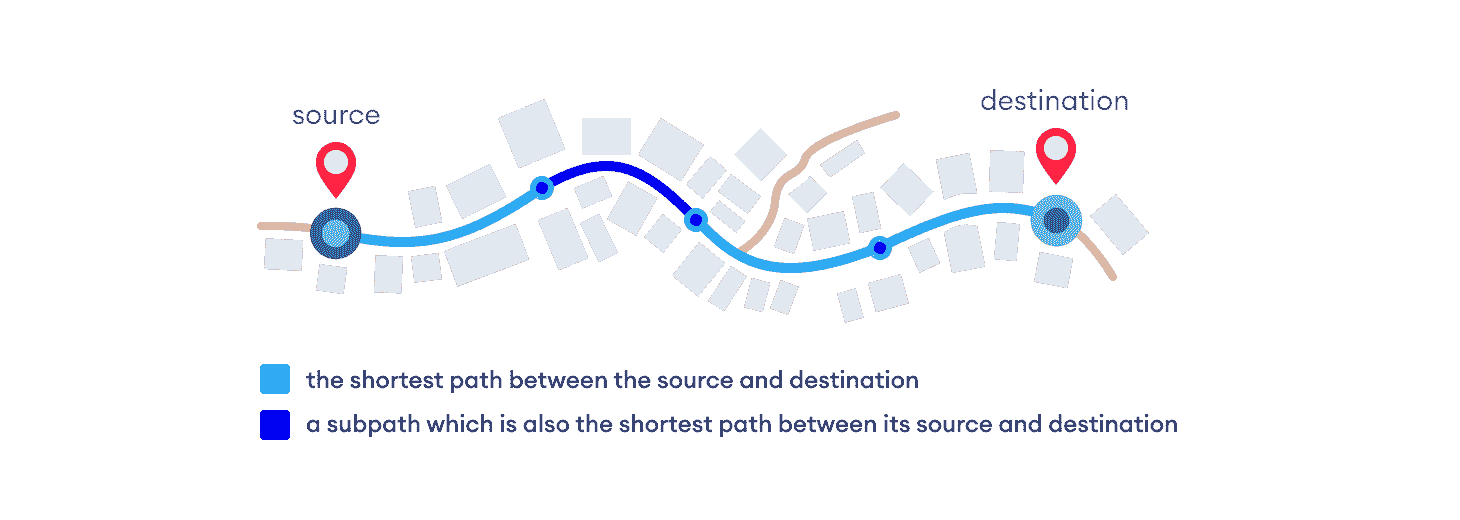
每个子路径是最短路径

Djikstra 在相反的方向上使用了此属性，即我们高估了每个顶点到起始顶点的距离。 然后，我们访问每个节点及其邻居，以找到到这些邻居的最短子路径。

该算法使用贪婪方法，因为我们找到了下一个最佳解决方案，希望最终结果是整个问题的最佳解决方案。

Dijkstra 算法的示例

从一个示例开始，然后考虑该算法会更容易。

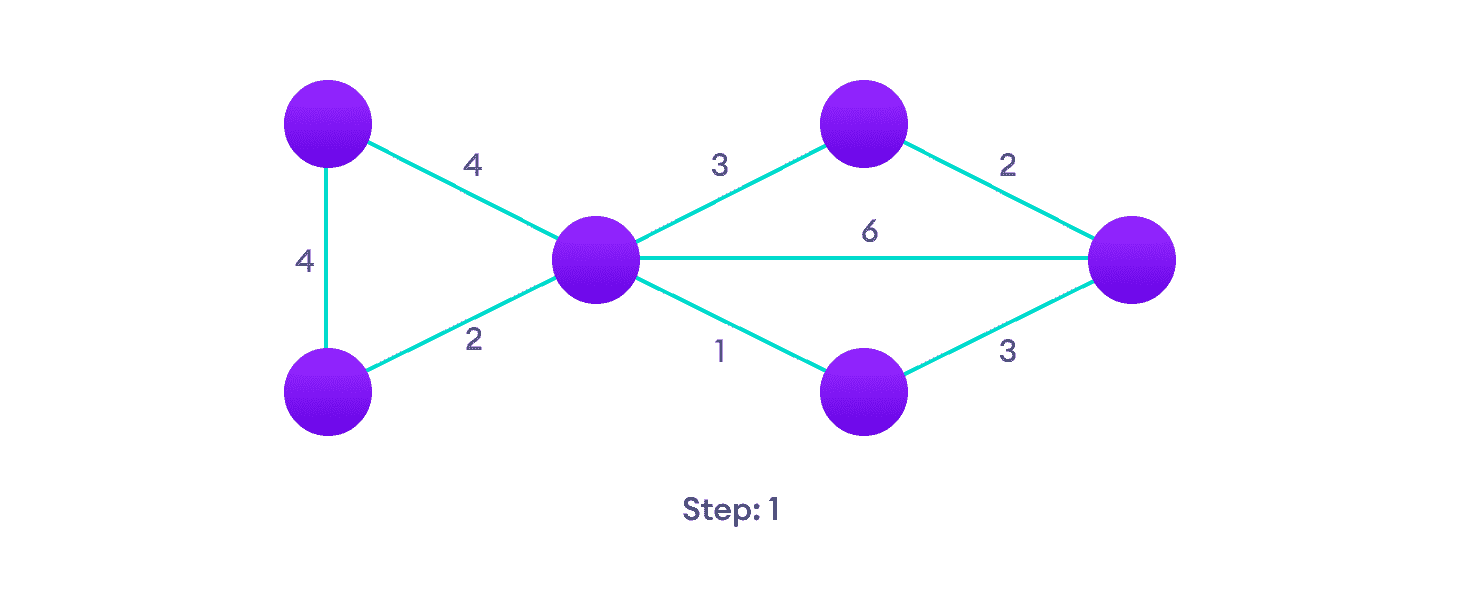
从加权图开始

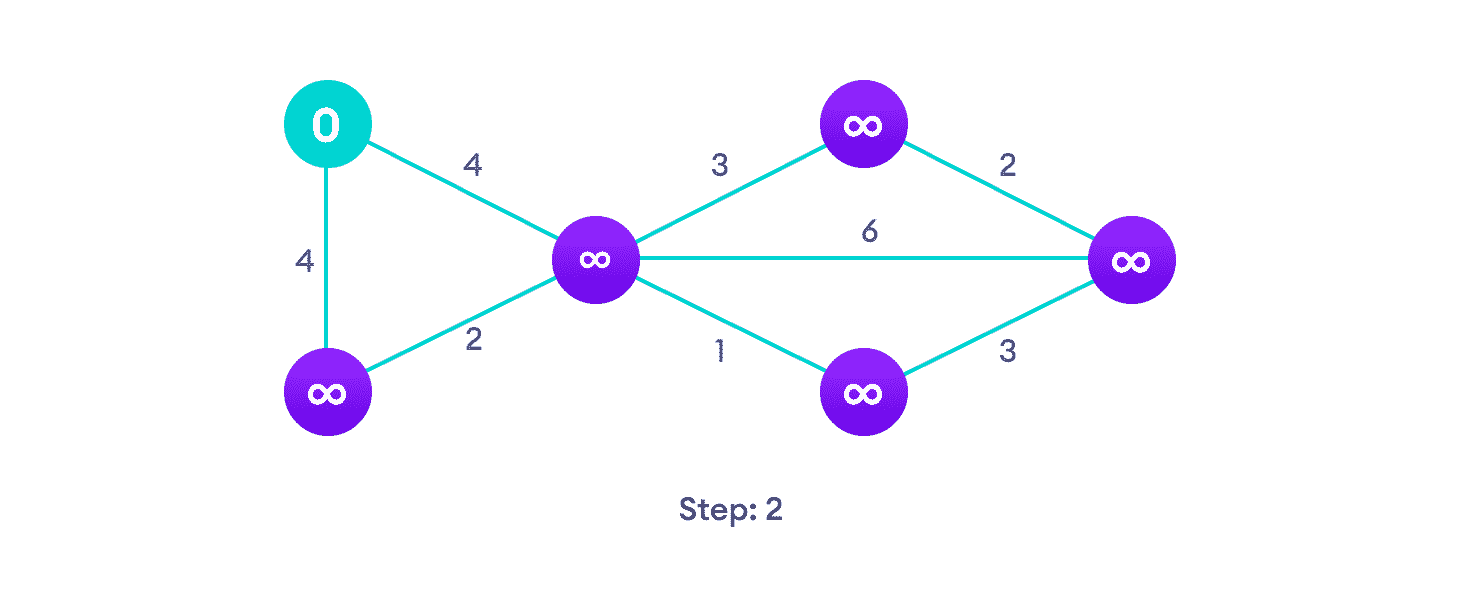
选择一个起始顶点并将无限路径值分配给所有其他设备

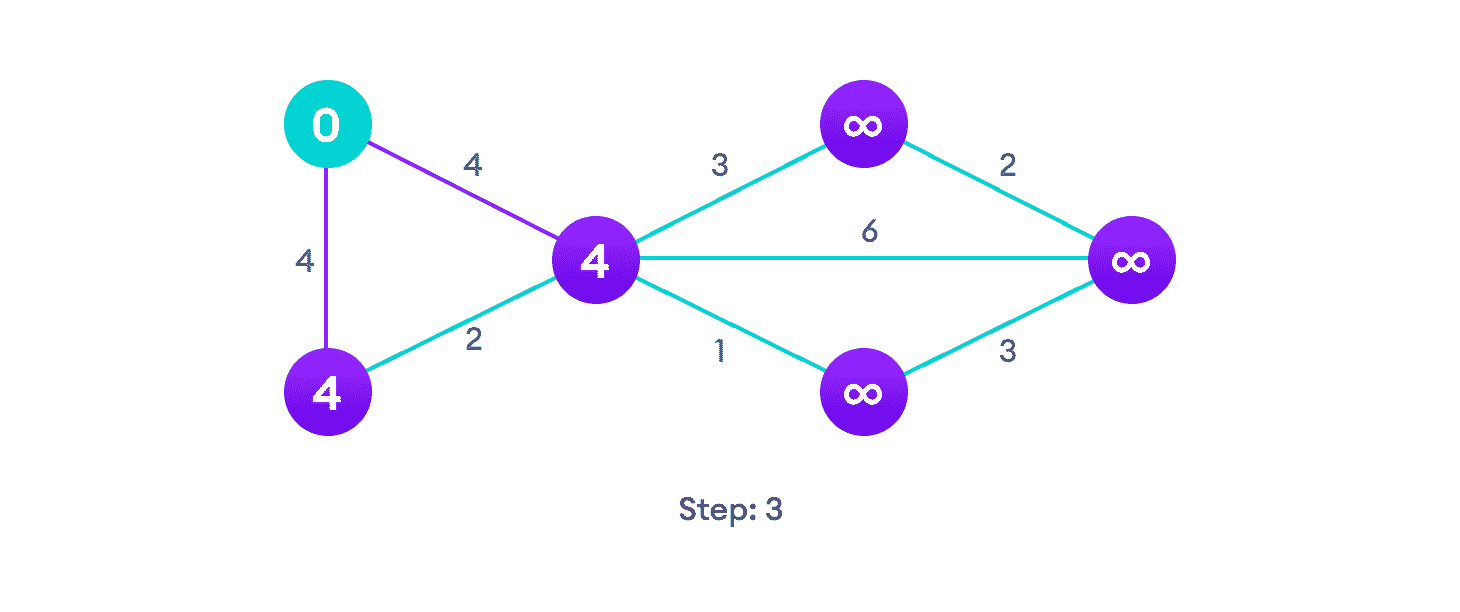
转到每个顶点并更新其路径长度

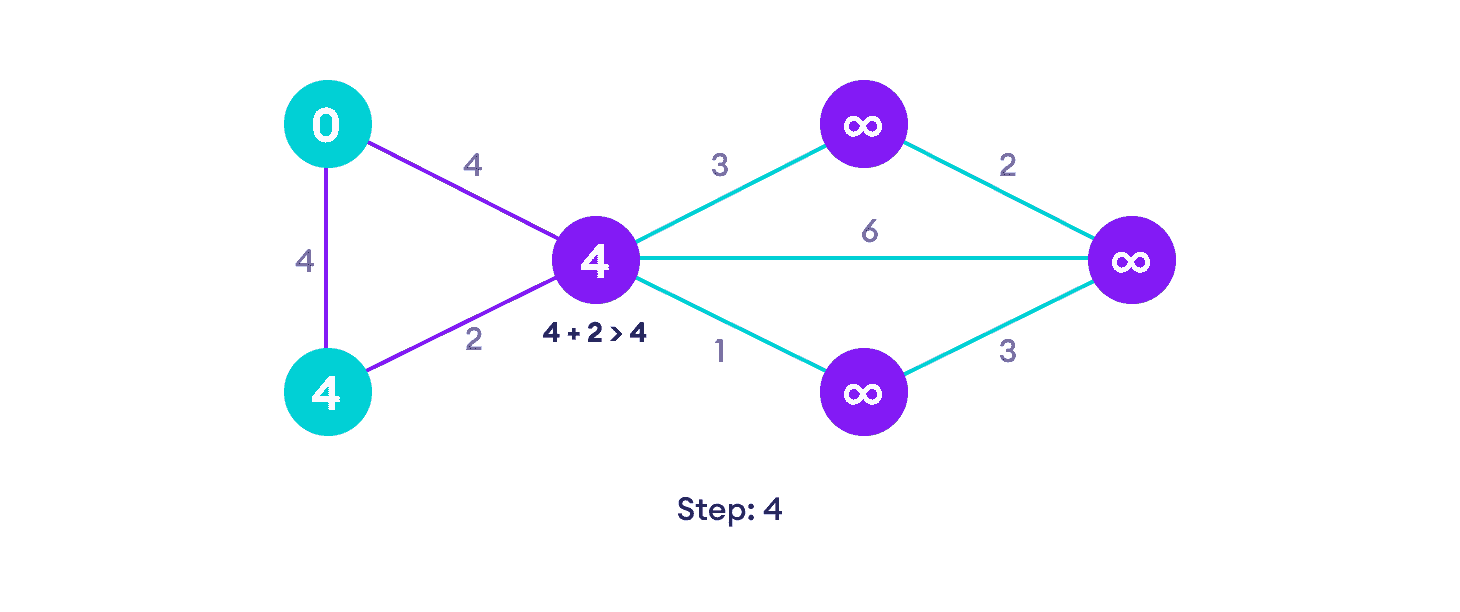
如果相邻顶点的路径长度小于新路径的长度，请不要更新它

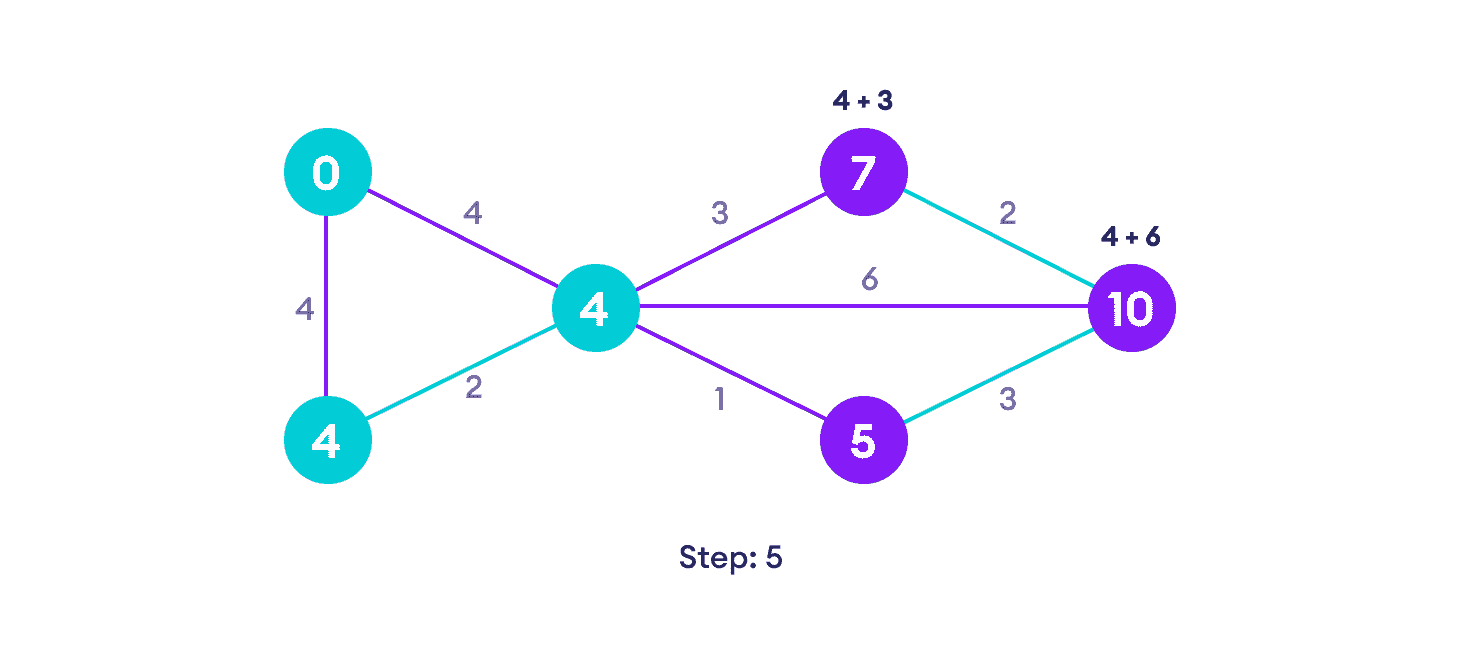
避免更新已访问顶点的路径长度

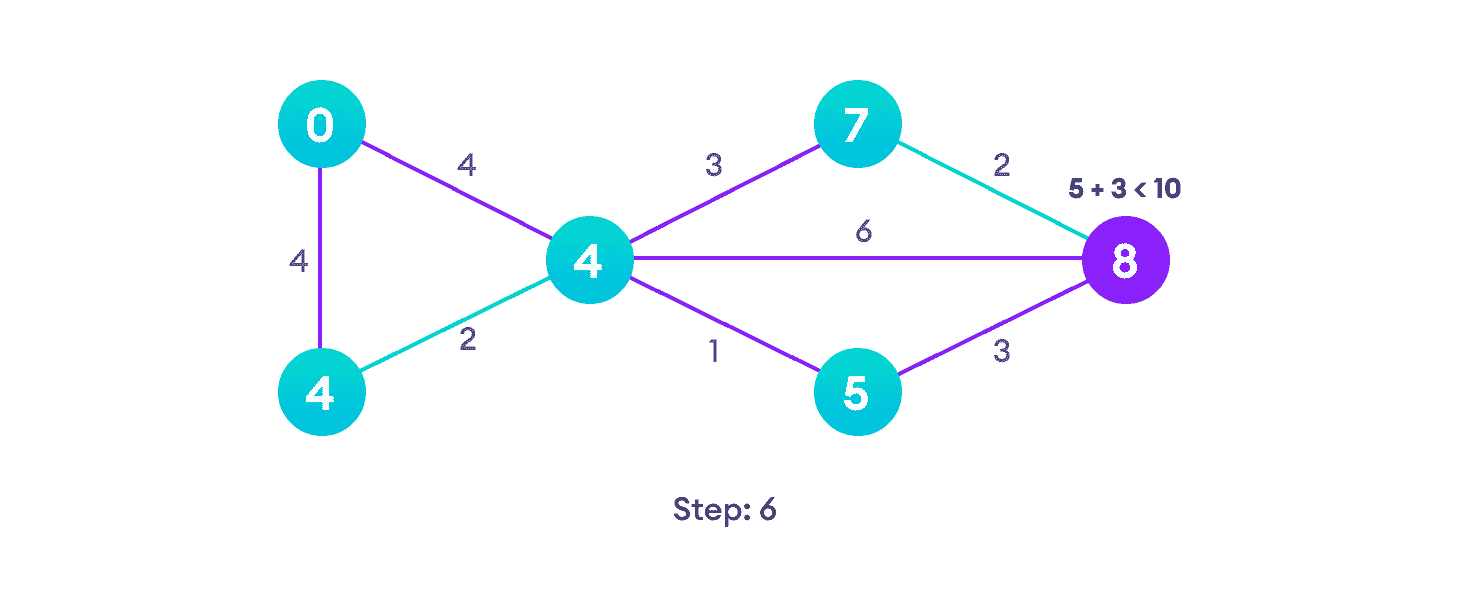
每次迭代后，我们选择路径长度最小的未访问顶点。 所以我们选择 7 之前的 5

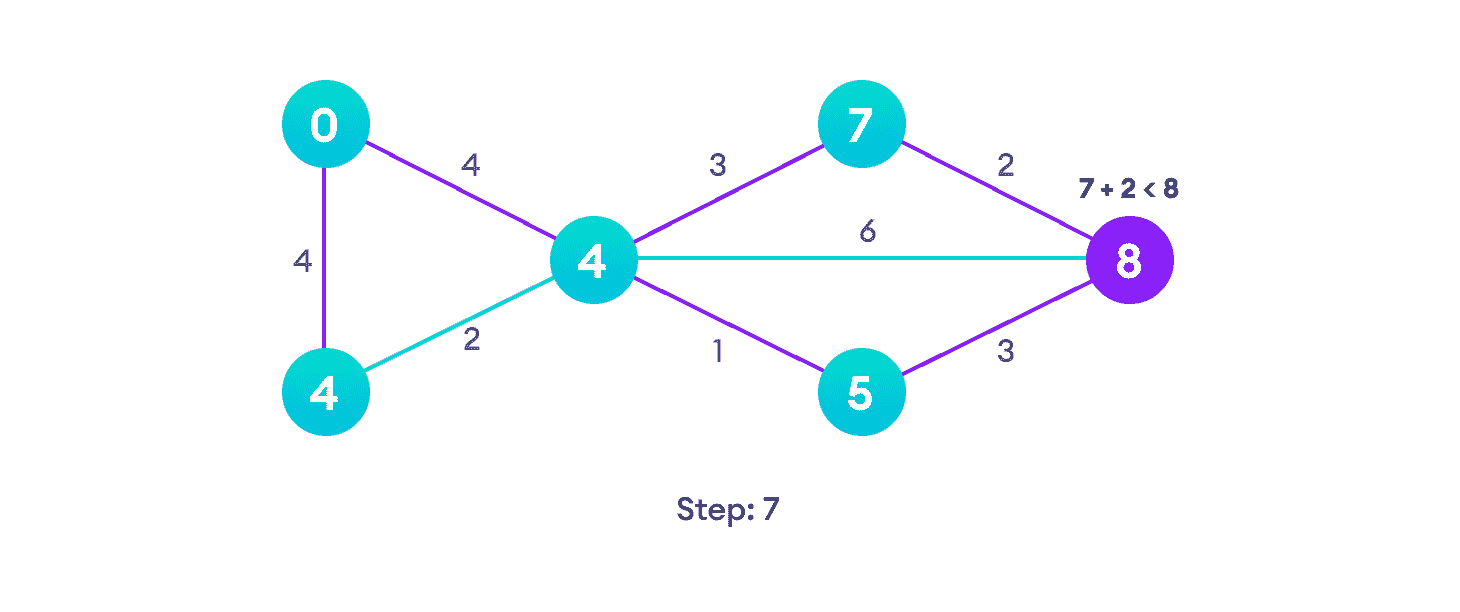
注意最右边的顶点的路径长度如何更新两次

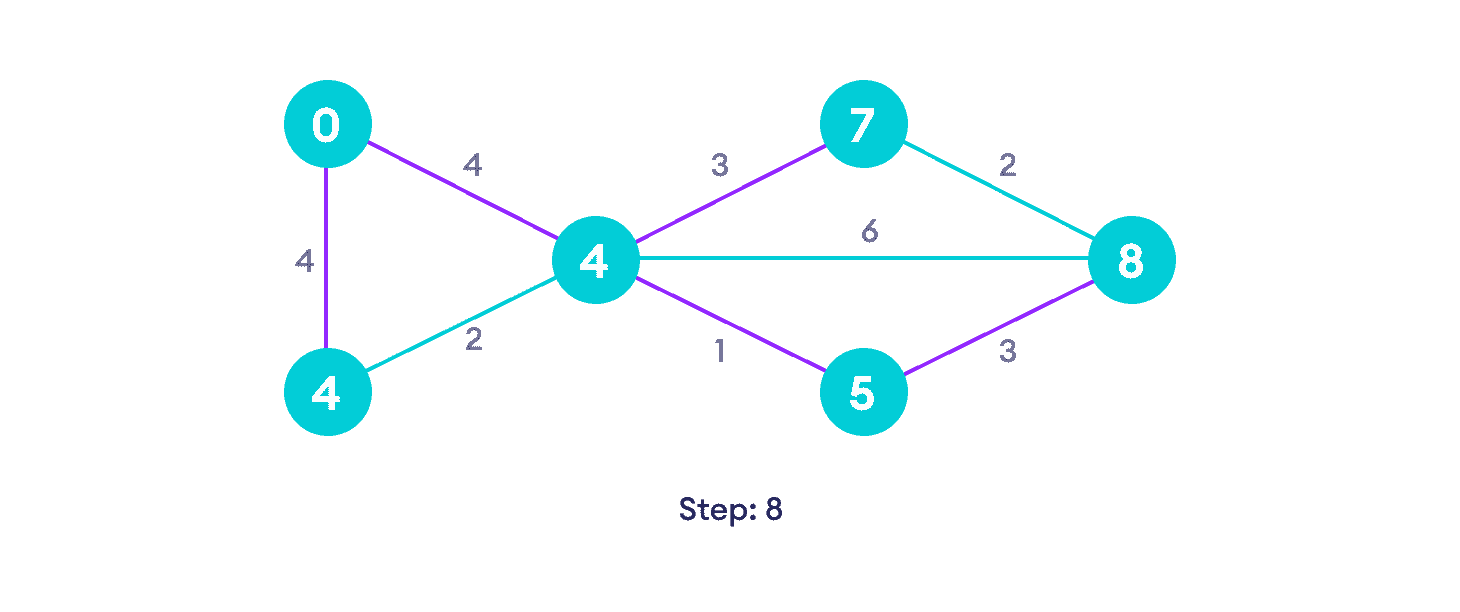
重复直到所有顶点都被访问

Djikstra 的算法伪代码

我们需要保持每个顶点的路径距离。 我们可以将其存储在大小为v的数组中，其中v是顶点数。

我们还希望能够获得最短路径，不仅知道最短路径的长度。 为此，我们将每个顶点映射到最后更新其路径长度的顶点。

算法结束后，我们可以从目标顶点回溯到源顶点以找到路径。

最小优先队列可用于以最小路径距离有效接收顶点。

function dijkstra(G, S)
    for each vertex V in G
        distance[V] <- infinite
        previous[V] <- NULL
        If V != S, add V to Priority Queue Q
    distance[S] <- 0
    while Q IS NOT EMPTY
        U <- Extract MIN from Q
        for each unvisited neighbour V of U
            tempDistance <- distance[U] + edge_weight(U, V)
            if tempDistance < distance[V]
                distance[V] <- tempDistance
                previous[V] <- U
    return distance[], previous[]

Dijkstra 算法的代码

下面给出了 Dijkstra 算法在 C++ 中的实现。 可以提高代码的复杂度，但是抽象方法很容易将代码与算法相关联。

# Dijkstra's Algorithm in Python

import sys

# Providing the graph
vertices = [[0, 0, 1, 1, 0, 0, 0],
            [0, 0, 1, 0, 0, 1, 0],
            [1, 1, 0, 1, 1, 0, 0],
            [1, 0, 1, 0, 0, 0, 1],
            [0, 0, 1, 0, 0, 1, 0],
            [0, 1, 0, 0, 1, 0, 1],
            [0, 0, 0, 1, 0, 1, 0]]

edges = [[0, 0, 1, 2, 0, 0, 0],
         [0, 0, 2, 0, 0, 3, 0],
         [1, 2, 0, 1, 3, 0, 0],
         [2, 0, 1, 0, 0, 0, 1],
         [0, 0, 3, 0, 0, 2, 0],
         [0, 3, 0, 0, 2, 0, 1],
         [0, 0, 0, 1, 0, 1, 0]]

# Find which vertex is to be visited next
def to_be_visited():
    global visited_and_distance
    v = -10
    for index in range(num_of_vertices):
        if visited_and_distance[index][0] == 0 \
            and (v < 0 or visited_and_distance[index][1] <=
                 visited_and_distance[v][1]):
            v = index
    return v

num_of_vertices = len(vertices[0])

visited_and_distance = [[0, 0]]
for i in range(num_of_vertices-1):
    visited_and_distance.append([0, sys.maxsize])

for vertex in range(num_of_vertices):

    # Find next vertex to be visited
    to_visit = to_be_visited()
    for neighbor_index in range(num_of_vertices):

        # Updating new distances
        if vertices[to_visit][neighbor_index] == 1 and \
                visited_and_distance[neighbor_index][0] == 0:
            new_distance = visited_and_distance[to_visit][1] \
                + edges[to_visit][neighbor_index]
            if visited_and_distance[neighbor_index][1] > new_distance:
                visited_and_distance[neighbor_index][1] = new_distance

        visited_and_distance[to_visit][0] = 1

i = 0

# Printing the distance
for distance in visited_and_distance:
    print("Distance of ", chr(ord('a') + i),
          " from source vertex: ", distance[1])
    i = i + 1

// Dijkstra's Algorithm in Java

public class Dijkstra {

  public static void dijkstra(int[][] graph, int source) {
    int count = graph.length;
    boolean[] visitedVertex = new boolean[count];
    int[] distance = new int[count];
    for (int i = 0; i < count; i++) {
      visitedVertex[i] = false;
      distance[i] = Integer.MAX_VALUE;
    }

    // Distance of self loop is zero
    distance[source] = 0;
    for (int i = 0; i < count; i++) {

      // Update the distance between neighbouring vertex and source vertex
      int u = findMinDistance(distance, visitedVertex);
      visitedVertex[u] = true;

      // Update all the neighbouring vertex distances
      for (int v = 0; v < count; v++) {
        if (!visitedVertex[v] && graph[u][v] != 0 && (distance[u] + graph[u][v] < distance[v])) {
          distance[v] = distance[u] + graph[u][v];
        }
      }
    }
    for (int i = 0; i < distance.length; i++) {
      System.out.println(String.format("Distance from %s to %s is %s", source, i, distance[i]));
    }

  }

  // Finding the minimum distance
  private static int findMinDistance(int[] distance, boolean[] visitedVertex) {
    int minDistance = Integer.MAX_VALUE;
    int minDistanceVertex = -1;
    for (int i = 0; i < distance.length; i++) {
      if (!visitedVertex[i] && distance[i] < minDistance) {
        minDistance = distance[i];
        minDistanceVertex = i;
      }
    }
    return minDistanceVertex;
  }

  public static void main(String[] args) {
    int graph[][] = new int[][] { { 0, 0, 1, 2, 0, 0, 0 }, { 0, 0, 2, 0, 0, 3, 0 }, { 1, 2, 0, 1, 3, 0, 0 },
        { 2, 0, 1, 0, 0, 0, 1 }, { 0, 0, 3, 0, 0, 2, 0 }, { 0, 3, 0, 0, 2, 0, 1 }, { 0, 0, 0, 1, 0, 1, 0 } };
    Dijkstra T = new Dijkstra();
    T.dijkstra(graph, 0);
  }
}

// Dijkstra's Algorithm in C

#include <stdio.h>
#define INFINITY 9999
#define MAX 10

void Dijkstra(int Graph[MAX][MAX], int n, int start);

void Dijkstra(int Graph[MAX][MAX], int n, int start) {
  int cost[MAX][MAX], distance[MAX], pred[MAX];
  int visited[MAX], count, mindistance, nextnode, i, j;

  // Creating cost matrix
  for (i = 0; i < n; i++)
    for (j = 0; j < n; j++)
      if (Graph[i][j] == 0)
        cost[i][j] = INFINITY;
      else
        cost[i][j] = Graph[i][j];

  for (i = 0; i < n; i++) {
    distance[i] = cost[start][i];
    pred[i] = start;
    visited[i] = 0;
  }

  distance[start] = 0;
  visited[start] = 1;
  count = 1;

  while (count < n - 1) {
    mindistance = INFINITY;

    for (i = 0; i < n; i++)
      if (distance[i] < mindistance && !visited[i]) {
        mindistance = distance[i];
        nextnode = i;
      }

    visited[nextnode] = 1;
    for (i = 0; i < n; i++)
      if (!visited[i])
        if (mindistance + cost[nextnode][i] < distance[i]) {
          distance[i] = mindistance + cost[nextnode][i];
          pred[i] = nextnode;
        }
    count++;
  }

  // Printing the distance
  for (i = 0; i < n; i++)
    if (i != start) {
      printf("\nDistance from source to %d: %d", i, distance[i]);
    }
}
int main() {
  int Graph[MAX][MAX], i, j, n, u;
  n = 7;

  Graph[0][0] = 0;
  Graph[0][1] = 0;
  Graph[0][2] = 1;
  Graph[0][3] = 2;
  Graph[0][4] = 0;
  Graph[0][5] = 0;
  Graph[0][6] = 0;

  Graph[1][0] = 0;
  Graph[1][1] = 0;
  Graph[1][2] = 2;
  Graph[1][3] = 0;
  Graph[1][4] = 0;
  Graph[1][5] = 3;
  Graph[1][6] = 0;

  Graph[2][0] = 1;
  Graph[2][1] = 2;
  Graph[2][2] = 0;
  Graph[2][3] = 1;
  Graph[2][4] = 3;
  Graph[2][5] = 0;
  Graph[2][6] = 0;

  Graph[3][0] = 2;
  Graph[3][1] = 0;
  Graph[3][2] = 1;
  Graph[3][3] = 0;
  Graph[3][4] = 0;
  Graph[3][5] = 0;
  Graph[3][6] = 1;

  Graph[4][0] = 0;
  Graph[4][1] = 0;
  Graph[4][2] = 3;
  Graph[4][3] = 0;
  Graph[4][4] = 0;
  Graph[4][5] = 2;
  Graph[4][6] = 0;

  Graph[5][0] = 0;
  Graph[5][1] = 3;
  Graph[5][2] = 0;
  Graph[5][3] = 0;
  Graph[5][4] = 2;
  Graph[5][5] = 0;
  Graph[5][6] = 1;

  Graph[6][0] = 0;
  Graph[6][1] = 0;
  Graph[6][2] = 0;
  Graph[6][3] = 1;
  Graph[6][4] = 0;
  Graph[6][5] = 1;
  Graph[6][6] = 0;

  u = 0;
  Dijkstra(Graph, n, u);

  return 0;
}

// Dijkstra's Algorithm in C++

#include <iostream>
#include <vector>

#define INT_MAX 10000000

using namespace std;

void DijkstrasTest();

int main() {
  DijkstrasTest();
  return 0;
}

class Node;
class Edge;

void Dijkstras();
vector<Node*>* AdjacentRemainingNodes(Node* node);
Node* ExtractSmallest(vector<Node*>& nodes);
int Distance(Node* node1, Node* node2);
bool Contains(vector<Node*>& nodes, Node* node);
void PrintShortestRouteTo(Node* destination);

vector<Node*> nodes;
vector<Edge*> edges;

class Node {
   public:
  Node(char id)
    : id(id), previous(NULL), distanceFromStart(INT_MAX) {
    nodes.push_back(this);
  }

   public:
  char id;
  Node* previous;
  int distanceFromStart;
};

class Edge {
   public:
  Edge(Node* node1, Node* node2, int distance)
    : node1(node1), node2(node2), distance(distance) {
    edges.push_back(this);
  }
  bool Connects(Node* node1, Node* node2) {
    return (
      (node1 == this->node1 &&
       node2 == this->node2) ||
      (node1 == this->node2 &&
       node2 == this->node1));
  }

   public:
  Node* node1;
  Node* node2;
  int distance;
};

///////////////////
void DijkstrasTest() {
  Node* a = new Node('a');
  Node* b = new Node('b');
  Node* c = new Node('c');
  Node* d = new Node('d');
  Node* e = new Node('e');
  Node* f = new Node('f');
  Node* g = new Node('g');

  Edge* e1 = new Edge(a, c, 1);
  Edge* e2 = new Edge(a, d, 2);
  Edge* e3 = new Edge(b, c, 2);
  Edge* e4 = new Edge(c, d, 1);
  Edge* e5 = new Edge(b, f, 3);
  Edge* e6 = new Edge(c, e, 3);
  Edge* e7 = new Edge(e, f, 2);
  Edge* e8 = new Edge(d, g, 1);
  Edge* e9 = new Edge(g, f, 1);

  a->distanceFromStart = 0;  // set start node
  Dijkstras();
  PrintShortestRouteTo(f);
}

///////////////////

void Dijkstras() {
  while (nodes.size() > 0) {
    Node* smallest = ExtractSmallest(nodes);
    vector<Node*>* adjacentNodes =
      AdjacentRemainingNodes(smallest);

    const int size = adjacentNodes->size();
    for (int i = 0; i < size; ++i) {
      Node* adjacent = adjacentNodes->at(i);
      int distance = Distance(smallest, adjacent) +
               smallest->distanceFromStart;

      if (distance < adjacent->distanceFromStart) {
        adjacent->distanceFromStart = distance;
        adjacent->previous = smallest;
      }
    }
    delete adjacentNodes;
  }
}

// Find the node with the smallest distance,
// remove it, and return it.
Node* ExtractSmallest(vector<Node*>& nodes) {
  int size = nodes.size();
  if (size == 0) return NULL;
  int smallestPosition = 0;
  Node* smallest = nodes.at(0);
  for (int i = 1; i < size; ++i) {
    Node* current = nodes.at(i);
    if (current->distanceFromStart <
      smallest->distanceFromStart) {
      smallest = current;
      smallestPosition = i;
    }
  }
  nodes.erase(nodes.begin() + smallestPosition);
  return smallest;
}

// Return all nodes adjacent to 'node' which are still
// in the 'nodes' collection.
vector<Node*>* AdjacentRemainingNodes(Node* node) {
  vector<Node*>* adjacentNodes = new vector<Node*>();
  const int size = edges.size();
  for (int i = 0; i < size; ++i) {
    Edge* edge = edges.at(i);
    Node* adjacent = NULL;
    if (edge->node1 == node) {
      adjacent = edge->node2;
    } else if (edge->node2 == node) {
      adjacent = edge->node1;
    }
    if (adjacent && Contains(nodes, adjacent)) {
      adjacentNodes->push_back(adjacent);
    }
  }
  return adjacentNodes;
}

// Return distance between two connected nodes
int Distance(Node* node1, Node* node2) {
  const int size = edges.size();
  for (int i = 0; i < size; ++i) {
    Edge* edge = edges.at(i);
    if (edge->Connects(node1, node2)) {
      return edge->distance;
    }
  }
  return -1;  // should never happen
}

// Does the 'nodes' vector contain 'node'
bool Contains(vector<Node*>& nodes, Node* node) {
  const int size = nodes.size();
  for (int i = 0; i < size; ++i) {
    if (node == nodes.at(i)) {
      return true;
    }
  }
  return false;
}

///////////////////

void PrintShortestRouteTo(Node* destination) {
  Node* previous = destination;
  cout << "Distance from start: "
     << destination->distanceFromStart << endl;
  while (previous) {
    cout << previous->id << " ";
    previous = previous->previous;
  }
  cout << endl;
}

// these two not needed
vector<Edge*>* AdjacentEdges(vector<Edge*>& Edges, Node* node);
void RemoveEdge(vector<Edge*>& Edges, Edge* edge);

vector<Edge*>* AdjacentEdges(vector<Edge*>& edges, Node* node) {
  vector<Edge*>* adjacentEdges = new vector<Edge*>();

  const int size = edges.size();
  for (int i = 0; i < size; ++i) {
    Edge* edge = edges.at(i);
    if (edge->node1 == node) {
      cout << "adjacent: " << edge->node2->id << endl;
      adjacentEdges->push_back(edge);
    } else if (edge->node2 == node) {
      cout << "adjacent: " << edge->node1->id << endl;
      adjacentEdges->push_back(edge);
    }
  }
  return adjacentEdges;
}

void RemoveEdge(vector<Edge*>& edges, Edge* edge) {
  vector<Edge*>::iterator it;
  for (it = edges.begin(); it < edges.end(); ++it) {
    if (*it == edge) {
      edges.erase(it);
      return;
    }
  }
}

Dijkstra 算法复杂度

时间复杂度：O(E Log V)

其中，E是边数，V是顶点数。

空间复杂度：O(V)

Dijkstra 算法应用

• 寻找最短路径
• 社交网络中的应用
• 在电话网中
• 在地图上查找位置