原文： https://www.programiz.com/dsa/kruskal-algorithm

在本教程中，您将学习 Kruskal 算法如何工作。 此外，您还将找到 C，C++ ，Java 和 Python 中 Kruskal 算法的工作示例。

Kruskal 算法是一种最小生成树算法，该算法将图形作为输入，并找到该图形的边子集，

  • 形成包括每个顶点的树
  • 在可以从图中形成的所有树中具有最小的权重总和

Kruskal 算法如何工作

它属于称为贪婪算法的一类算法，该算法可以找到局部最优值，以期找到全局最优值。

我们从权重最低的边开始，不断增加边直到达到目标。

实现 Kruskal 算法的步骤如下：

  1. 从小到大排序所有边
  2. 选取权重最低的边并将其添加到生成树。 如果添加边创建了一个循环，则拒绝该边。
  3. 继续添加边，直到我们到达所有顶点。

Kruskal 算法的示例

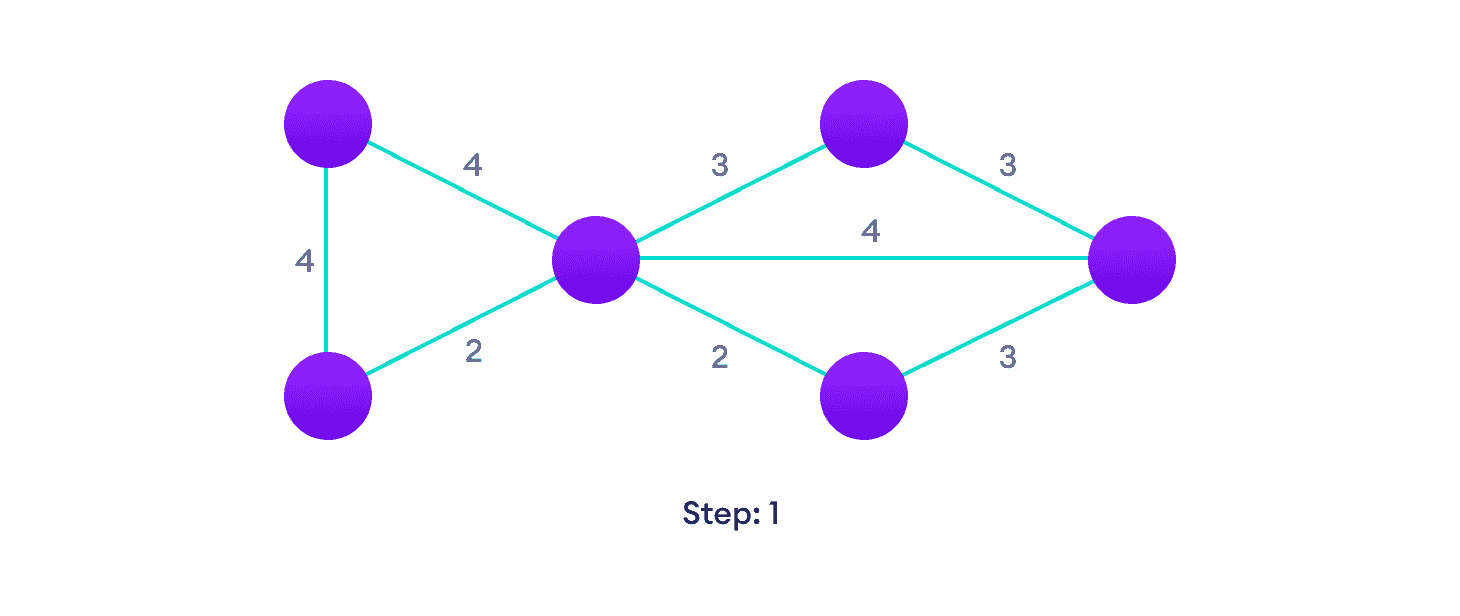
Kruskal 算法 - 图1

从加权图开始

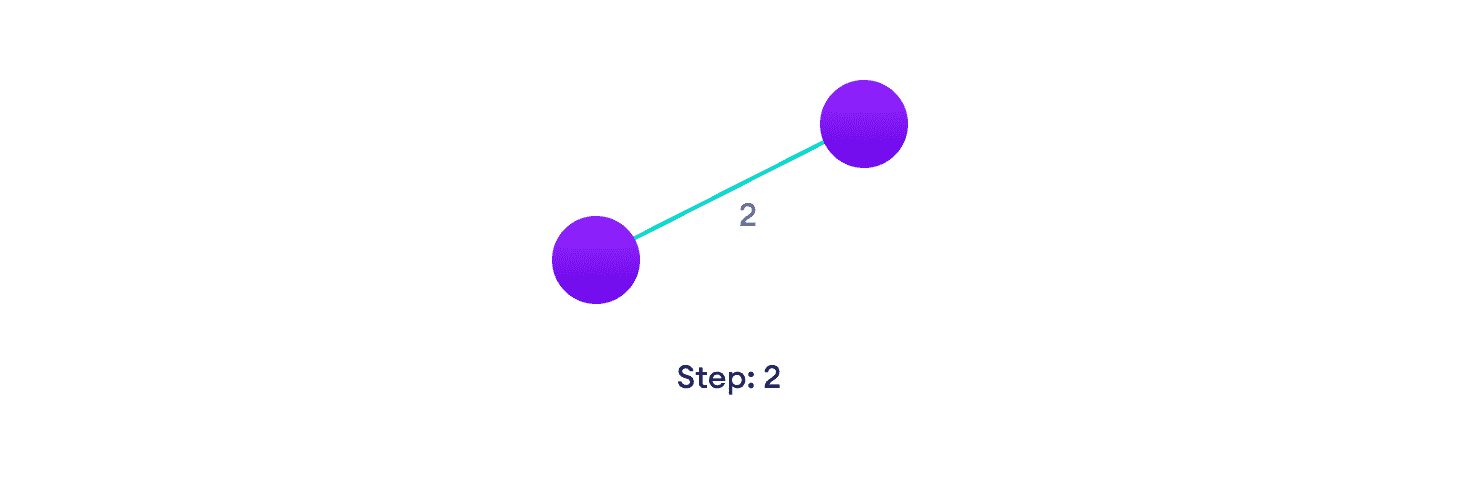
Kruskal 算法 - 图2

选择重量最小的边，如果大于 1，则选择任何东西

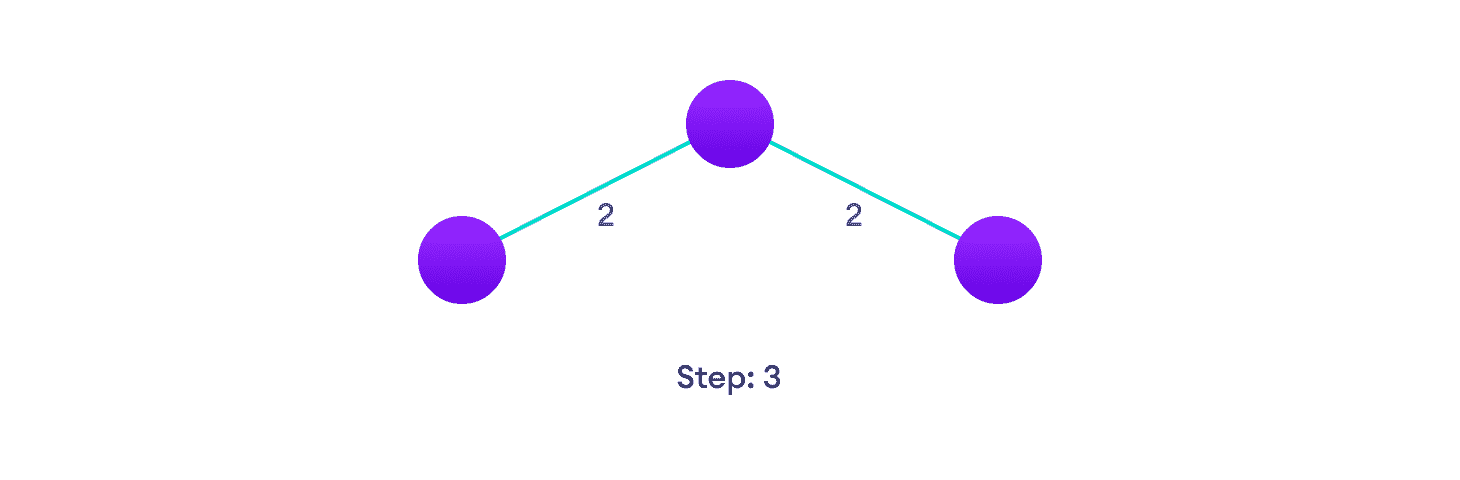
Kruskal 算法 - 图3

选择下一个最短边并添加

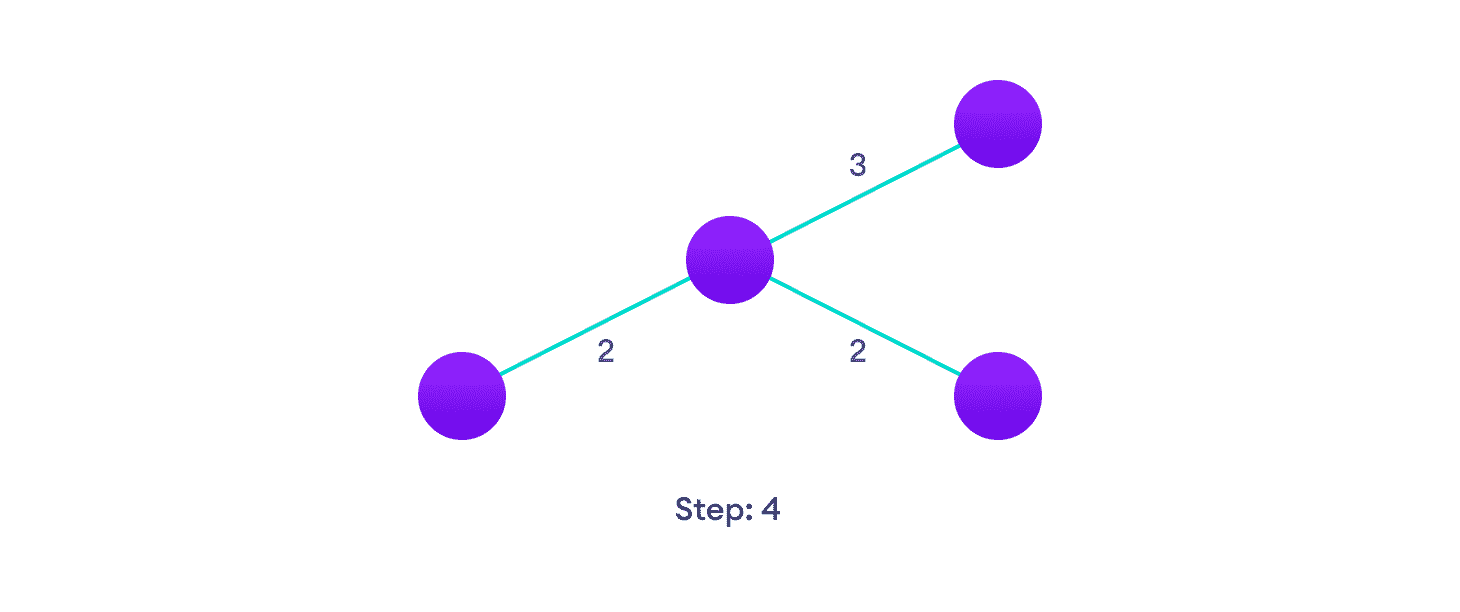
Kruskal 算法 - 图4

选择下一个最短边并添加

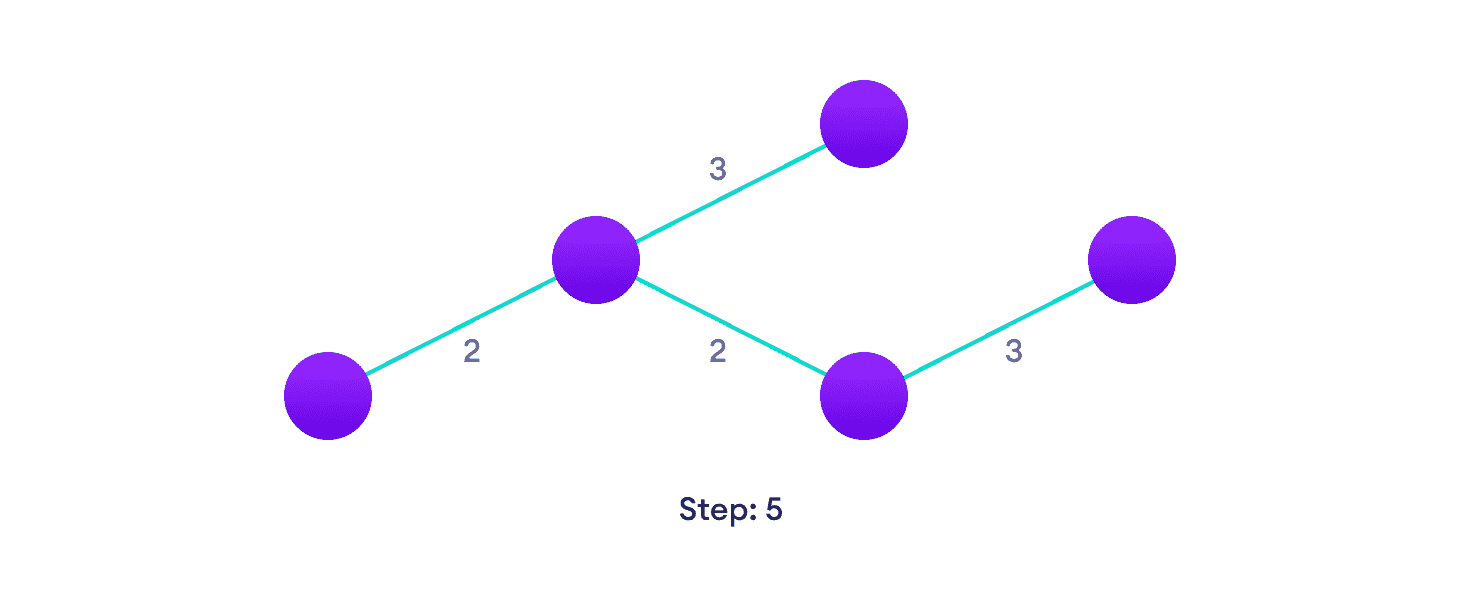
Kruskal 算法 - 图5

选择下一个最短边并添加

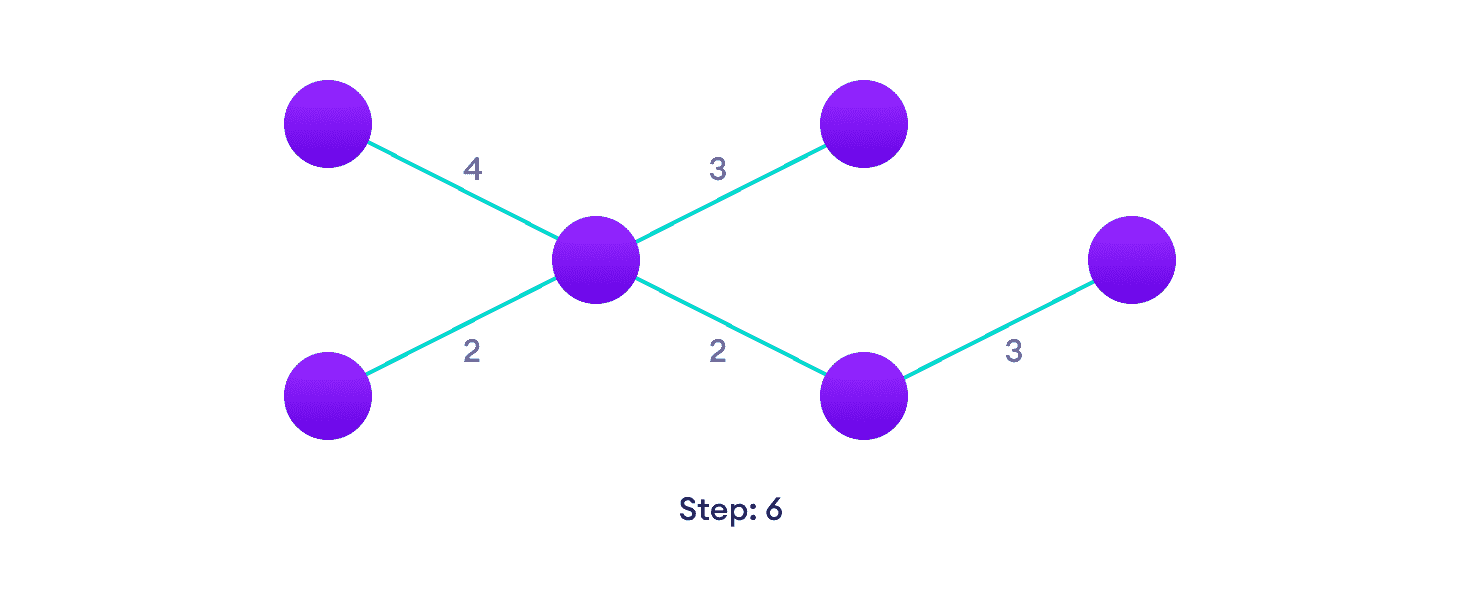
Kruskal 算法 - 图6

重复直到您有一棵生成树

Kruskal 算法伪代码

任何最小生成树算法都围绕检查是否添加边创建循环来进行。

最常见的查找方法是称为 UnionFind 的算法。 Union-Find 算法将顶点划分为簇，并允许我们检查两个顶点是否属于同一簇，从而确定是否添加边会创建一个循环。

  1. KRUSKAL(G):
  2. A = ∅
  3. For each vertex v ∈ G.V:
  4.     MAKE-SET(v)
  5. For each edge (u, v) ∈ G.E ordered by increasing order by weight(u, v):
  6.     if FIND-SET(u) ≠ FIND-SET(v):       
  7.     A = A ∪ {(u, v)}
  8.     UNION(u, v)
  9. return A

Python，Java 和 C/C++ 示例

# Kruskal's algorithm in Python

class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = []

    def add_edge(self, u, v, w):
        self.graph.append([u, v, w])

    # Search function

    def find(self, parent, i):
        if parent[i] == i:
            return i
        return self.find(parent, parent[i])

    def apply_union(self, parent, rank, x, y):
        xroot = self.find(parent, x)
        yroot = self.find(parent, y)
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot
        else:
            parent[yroot] = xroot
            rank[xroot] += 1

    #  Applying Kruskal algorithm
    def kruskal_algo(self):
        result = []
        i, e = 0, 0
        self.graph = sorted(self.graph, key=lambda item: item[2])
        parent = []
        rank = []
        for node in range(self.V):
            parent.append(node)
            rank.append(0)
        while e < self.V - 1:
            u, v, w = self.graph[i]
            i = i + 1
            x = self.find(parent, u)
            y = self.find(parent, v)
            if x != y:
                e = e + 1
                result.append([u, v, w])
                self.apply_union(parent, rank, x, y)
        for u, v, weight in result:
            print("%d - %d: %d" % (u, v, weight))

g = Graph(6)
g.add_edge(0, 1, 4)
g.add_edge(0, 2, 4)
g.add_edge(1, 2, 2)
g.add_edge(1, 0, 4)
g.add_edge(2, 0, 4)
g.add_edge(2, 1, 2)
g.add_edge(2, 3, 3)
g.add_edge(2, 5, 2)
g.add_edge(2, 4, 4)
g.add_edge(3, 2, 3)
g.add_edge(3, 4, 3)
g.add_edge(4, 2, 4)
g.add_edge(4, 3, 3)
g.add_edge(5, 2, 2)
g.add_edge(5, 4, 3)
g.kruskal_algo()

// Kruskal's algorithm in Java

import java.util.*;

class Graph {
  class Edge implements Comparable<Edge> {
    int src, dest, weight;

    public int compareTo(Edge compareEdge) {
      return this.weight - compareEdge.weight;
    }
  };

  // Union
  class subset {
    int parent, rank;
  };

  int vertices, edges;
  Edge edge[];

  // Graph creation
  Graph(int v, int e) {
    vertices = v;
    edges = e;
    edge = new Edge[edges];
    for (int i = 0; i < e; ++i)
      edge[i] = new Edge();
  }

  int find(subset subsets[], int i) {
    if (subsets[i].parent != i)
      subsets[i].parent = find(subsets, subsets[i].parent);
    return subsets[i].parent;
  }

  void Union(subset subsets[], int x, int y) {
    int xroot = find(subsets, x);
    int yroot = find(subsets, y);

    if (subsets[xroot].rank < subsets[yroot].rank)
      subsets[xroot].parent = yroot;
    else if (subsets[xroot].rank > subsets[yroot].rank)
      subsets[yroot].parent = xroot;
    else {
      subsets[yroot].parent = xroot;
      subsets[xroot].rank++;
    }
  }

  // Applying Krushkal Algorithm
  void KruskalAlgo() {
    Edge result[] = new Edge[vertices];
    int e = 0;
    int i = 0;
    for (i = 0; i < vertices; ++i)
      result[i] = new Edge();

    // Sorting the edges
    Arrays.sort(edge);
    subset subsets[] = new subset[vertices];
    for (i = 0; i < vertices; ++i)
      subsets[i] = new subset();

    for (int v = 0; v < vertices; ++v) {
      subsets[v].parent = v;
      subsets[v].rank = 0;
    }
    i = 0;
    while (e < vertices - 1) {
      Edge next_edge = new Edge();
      next_edge = edge[i++];
      int x = find(subsets, next_edge.src);
      int y = find(subsets, next_edge.dest);
      if (x != y) {
        result[e++] = next_edge;
        Union(subsets, x, y);
      }
    }
    for (i = 0; i < e; ++i)
      System.out.println(result[i].src + " - " + result[i].dest + ": " + result[i].weight);
  }

  public static void main(String[] args) {
    int vertices = 6; // Number of vertices
    int edges = 8; // Number of edges
    Graph G = new Graph(vertices, edges);

    G.edge[0].src = 0;
    G.edge[0].dest = 1;
    G.edge[0].weight = 4;

    G.edge[1].src = 0;
    G.edge[1].dest = 2;
    G.edge[1].weight = 4;

    G.edge[2].src = 1;
    G.edge[2].dest = 2;
    G.edge[2].weight = 2;

    G.edge[3].src = 2;
    G.edge[3].dest = 3;
    G.edge[3].weight = 3;

    G.edge[4].src = 2;
    G.edge[4].dest = 5;
    G.edge[4].weight = 2;

    G.edge[5].src = 2;
    G.edge[5].dest = 4;
    G.edge[5].weight = 4;

    G.edge[6].src = 3;
    G.edge[6].dest = 4;
    G.edge[6].weight = 3;

    G.edge[7].src = 5;
    G.edge[7].dest = 4;
    G.edge[7].weight = 3;
    G.KruskalAlgo();
  }
}

// Kruskal's algorithm in C

#include <stdio.h>

#define MAX 30

typedef struct edge {
  int u, v, w;
} edge;

typedef struct edge_list {
  edge data[MAX];
  int n;
} edge_list;

edge_list elist;

int Graph[MAX][MAX], n;
edge_list spanlist;

void kruskalAlgo();
int find(int belongs[], int vertexno);
void applyUnion(int belongs[], int c1, int c2);
void sort();
void print();

// Applying Krushkal Algo
void kruskalAlgo() {
  int belongs[MAX], i, j, cno1, cno2;
  elist.n = 0;

  for (i = 1; i < n; i++)
    for (j = 0; j < i; j++) {
      if (Graph[i][j] != 0) {
        elist.data[elist.n].u = i;
        elist.data[elist.n].v = j;
        elist.data[elist.n].w = Graph[i][j];
        elist.n++;
      }
    }

  sort();

  for (i = 0; i < n; i++)
    belongs[i] = i;

  spanlist.n = 0;

  for (i = 0; i < elist.n; i++) {
    cno1 = find(belongs, elist.data[i].u);
    cno2 = find(belongs, elist.data[i].v);

    if (cno1 != cno2) {
      spanlist.data[spanlist.n] = elist.data[i];
      spanlist.n = spanlist.n + 1;
      applyUnion(belongs, cno1, cno2);
    }
  }
}

int find(int belongs[], int vertexno) {
  return (belongs[vertexno]);
}

void applyUnion(int belongs[], int c1, int c2) {
  int i;

  for (i = 0; i < n; i++)
    if (belongs[i] == c2)
      belongs[i] = c1;
}

// Sorting algo
void sort() {
  int i, j;
  edge temp;

  for (i = 1; i < elist.n; i++)
    for (j = 0; j < elist.n - 1; j++)
      if (elist.data[j].w > elist.data[j + 1].w) {
        temp = elist.data[j];
        elist.data[j] = elist.data[j + 1];
        elist.data[j + 1] = temp;
      }
}

// Printing the result
void print() {
  int i, cost = 0;

  for (i = 0; i < spanlist.n; i++) {
    printf("\n%d - %d : %d", spanlist.data[i].u, spanlist.data[i].v, spanlist.data[i].w);
    cost = cost + spanlist.data[i].w;
  }

  printf("\nSpanning tree cost: %d", cost);
}

int main() {
  int i, j, total_cost;

  n = 6;

  Graph[0][0] = 0;
  Graph[0][1] = 4;
  Graph[0][2] = 4;
  Graph[0][3] = 0;
  Graph[0][4] = 0;
  Graph[0][5] = 0;
  Graph[0][6] = 0;

  Graph[1][0] = 4;
  Graph[1][1] = 0;
  Graph[1][2] = 2;
  Graph[1][3] = 0;
  Graph[1][4] = 0;
  Graph[1][5] = 0;
  Graph[1][6] = 0;

  Graph[2][0] = 4;
  Graph[2][1] = 2;
  Graph[2][2] = 0;
  Graph[2][3] = 3;
  Graph[2][4] = 4;
  Graph[2][5] = 0;
  Graph[2][6] = 0;

  Graph[3][0] = 0;
  Graph[3][1] = 0;
  Graph[3][2] = 3;
  Graph[3][3] = 0;
  Graph[3][4] = 3;
  Graph[3][5] = 0;
  Graph[3][6] = 0;

  Graph[4][0] = 0;
  Graph[4][1] = 0;
  Graph[4][2] = 4;
  Graph[4][3] = 3;
  Graph[4][4] = 0;
  Graph[4][5] = 0;
  Graph[4][6] = 0;

  Graph[5][0] = 0;
  Graph[5][1] = 0;
  Graph[5][2] = 2;
  Graph[5][3] = 0;
  Graph[5][4] = 3;
  Graph[5][5] = 0;
  Graph[5][6] = 0;

  kruskalAlgo();
  print();
}

// Kruskal's algorithm in C++

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

#define edge pair<int, int>

class Graph {
   private:
  vector<pair<int, edge> > G;  // graph
  vector<pair<int, edge> > T;  // mst
  int *parent;
  int V;  // number of vertices/nodes in graph
   public:
  Graph(int V);
  void AddWeightedEdge(int u, int v, int w);
  int find_set(int i);
  void union_set(int u, int v);
  void kruskal();
  void print();
};
Graph::Graph(int V) {
  parent = new int[V];

  //i 0 1 2 3 4 5
  //parent[i] 0 1 2 3 4 5
  for (int i = 0; i < V; i++)
    parent[i] = i;

  G.clear();
  T.clear();
}
void Graph::AddWeightedEdge(int u, int v, int w) {
  G.push_back(make_pair(w, edge(u, v)));
}
int Graph::find_set(int i) {
  // If i is the parent of itself
  if (i == parent[i])
    return i;
  else
    // Else if i is not the parent of itself
    // Then i is not the representative of his set,
    // so we recursively call Find on its parent
    return find_set(parent[i]);
}

void Graph::union_set(int u, int v) {
  parent[u] = parent[v];
}
void Graph::kruskal() {
  int i, uRep, vRep;
  sort(G.begin(), G.end());  // increasing weight
  for (i = 0; i < G.size(); i++) {
    uRep = find_set(G[i].second.first);
    vRep = find_set(G[i].second.second);
    if (uRep != vRep) {
      T.push_back(G[i]);  // add to tree
      union_set(uRep, vRep);
    }
  }
}
void Graph::print() {
  cout << "Edge :"
     << " Weight" << endl;
  for (int i = 0; i < T.size(); i++) {
    cout << T[i].second.first << " - " << T[i].second.second << " : "
       << T[i].first;
    cout << endl;
  }
}
int main() {
  Graph g(6);
  g.AddWeightedEdge(0, 1, 4);
  g.AddWeightedEdge(0, 2, 4);
  g.AddWeightedEdge(1, 2, 2);
  g.AddWeightedEdge(1, 0, 4);
  g.AddWeightedEdge(2, 0, 4);
  g.AddWeightedEdge(2, 1, 2);
  g.AddWeightedEdge(2, 3, 3);
  g.AddWeightedEdge(2, 5, 2);
  g.AddWeightedEdge(2, 4, 4);
  g.AddWeightedEdge(3, 2, 3);
  g.AddWeightedEdge(3, 4, 3);
  g.AddWeightedEdge(4, 2, 4);
  g.AddWeightedEdge(4, 3, 3);
  g.AddWeightedEdge(5, 2, 2);
  g.AddWeightedEdge(5, 4, 3);
  g.kruskal();
  g.print();
  return 0;
}

Kruskal vs Prim 算法

Prim 算法是另一种流行的最小生成树算法，它使用不同的逻辑来查找图的 MST。 Prim 的算法不是从边开始，而是从顶点开始，并不断添加树中没有的权重最低的边，直到所有顶点都被覆盖为止。

Kruskal 算法的复杂度

Kruskal 算法的时间复杂度为：O(E log E)。

Kruskal 算法的应用

  • 为了布置电线
  • 在计算机网络中（LAN 连接）