渐近分析

原文： https://www.programiz.com/dsa/asymptotic-notations

算法的效率取决于执行算法所需的时间，存储空间和其他资源。借助渐近符号来测量效率。

对于不同类型的输入，算法可能不会具有相同的性能。随着输入大小的增加，性能将会改变。

将算法性能随输入大小顺序的变化而进行的研究定义为渐近分析。

渐近符号

渐进符号是当输入趋于特定值或极限值时用于描述算法运行时间的数学符号。

例如：在冒泡排序中，当输入数组已经排序时，算法花费的时间是线性的，即最佳情况。

但是，当输入数组处于反向条件时，该算法将花费最大时间（二次）对元素进行排序，即最坏的情况。

当输入数组既未排序也不反向时，则需要平均时间。这些持续时间使用渐近符号表示。

主要有三种渐近符号：Theta 符号，Omega 符号和大 O 符号。

Theta 表示法从上方和下方将函数括起来。由于它代表算法运行时间的上限和下限，因此可用于分析算法的平均用例复杂度。

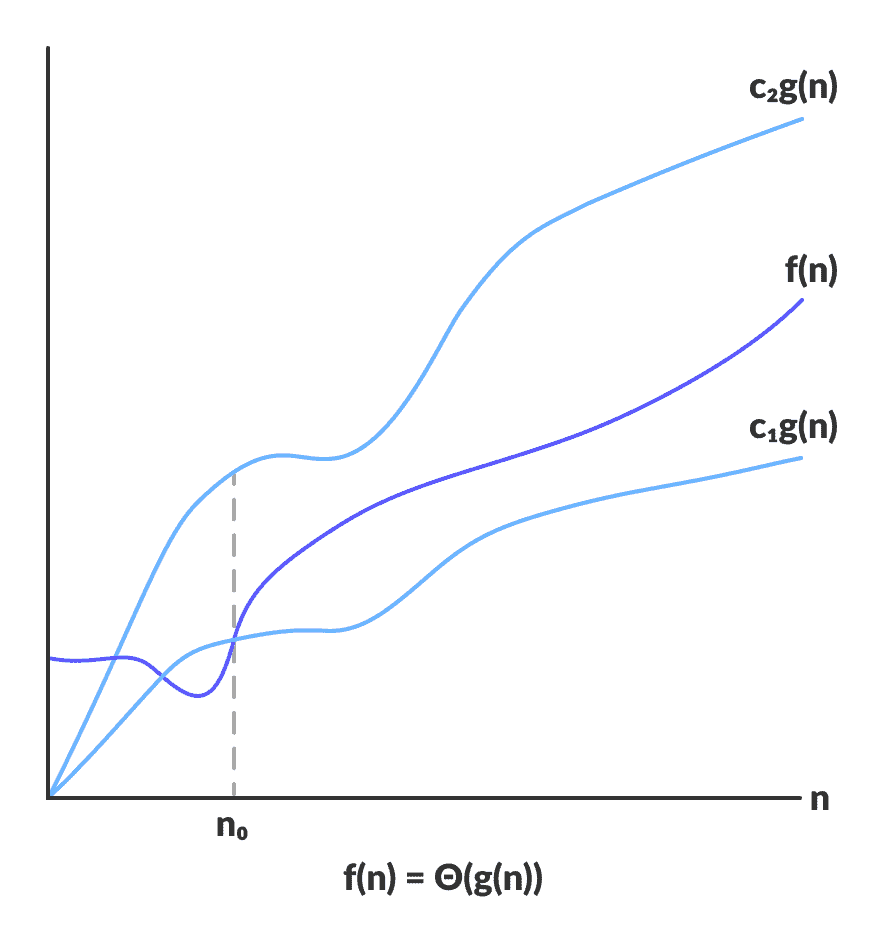
渐近分析 - 图1

Theta 将函数限制在常数因子之内

对于函数g(n)，Θ(g(n))由以下关系式给出：

Θ(g(n)) = { f(n): there exist positive constants c1, c2 and n0
            such that 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) for all n ≥ n0 }

如果存在正常数c1和c2，使得可以将其夹在c1g(n)和c2g(n)之间，则对于足够大的n，可以将上述表达式描述为函数f(n)属于集合Θ(g(n))。

如果对于所有n ≥ n0，函数f(n)位于c1g(n)和c2 > g(n)之间，则f(n)渐近严格。

大 O 表示法表示算法运行时间的上限。因此，它给出了算法的最坏情况的复杂度。

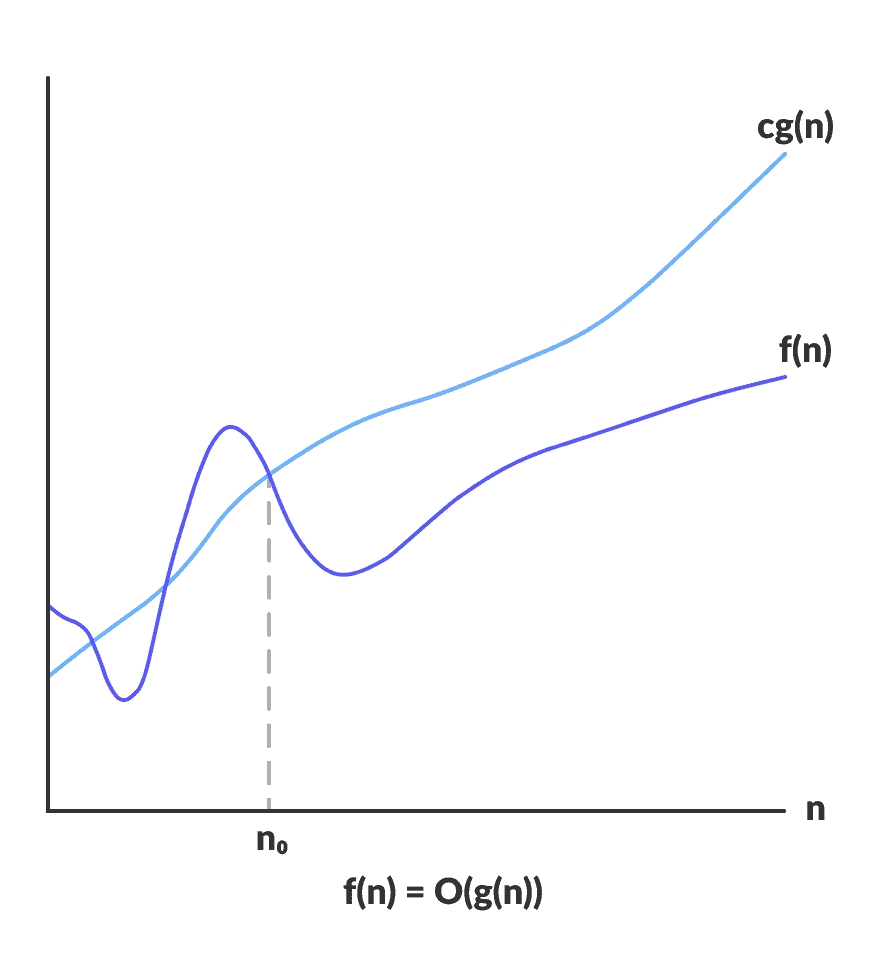
渐近分析 - 图2

大 O 给出函数的上限

O(g(n)) = { f(n): there exist positive constants c and n0
            such that 0 ≤ f(n) ≤ cg(n) for all n ≥ n0 }

对于存在足够大的n的情况，如果存在正常数c使得其位于0和cg(n)之间，则上述表达式可以被描述为函数f(n)属于集合O(g(n))。

对于n的任何值，算法的运行时间不会与O(g(n))提供的时间交叉。

由于它给出了算法的最坏情况下的运行时间，因此它被广泛用于分析算法，因为我们一直对最坏情况下的场景感兴趣。

Ω 表示算法运行时间的下限。因此，它提供了算法的最佳情况复杂度。

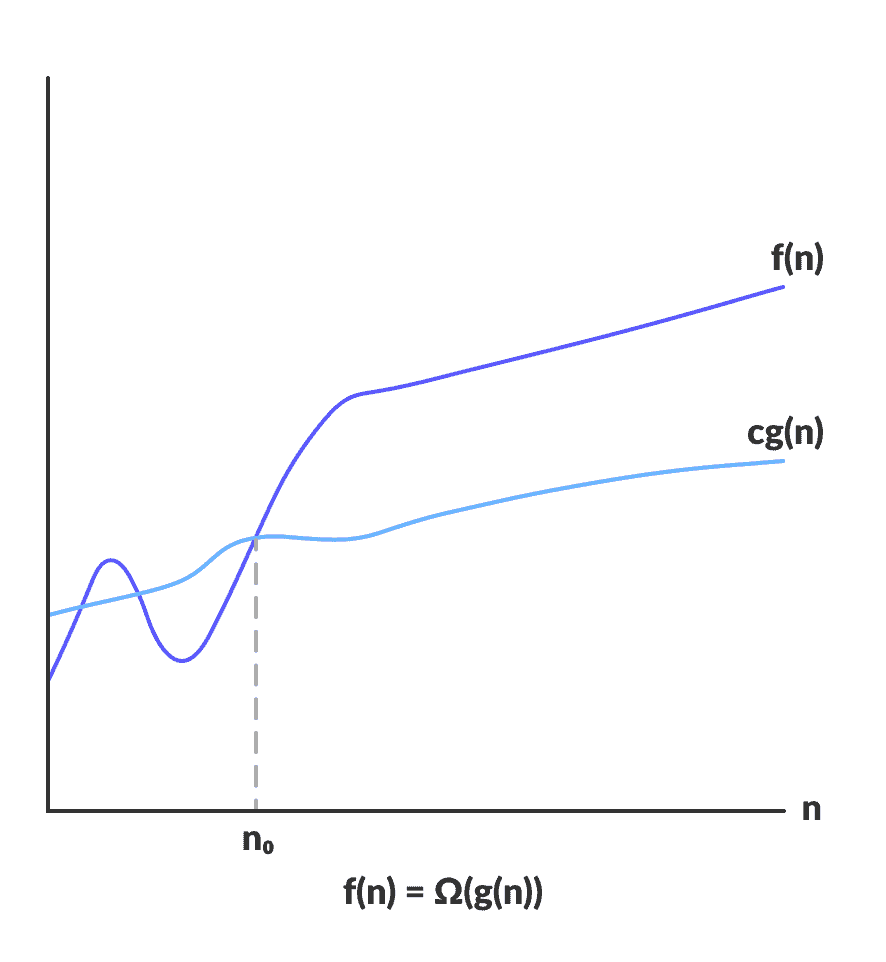
渐近分析 - 图3

Ω 给出函数的下限

Ω(g(n)) = { f(n): there exist positive constants c and n0 
            such that 0 ≤ cg(n) ≤ f(n) for all n ≥ n0 }

如果存在足够大的n，如果存在正常数c使得它位于cg(n)之上，则上述表达式可以描述为函数f(n)属于集合Ω(g(n))。

对于n的任何值，算法所需的最短时间由 Omega Ω(g(n))给出。