原文： https://www.programiz.com/dsa/insertion-into-a-b-tree

在本教程中，您将学习如何将键插入 B 树。 此外，您还将找到在 C，C++ ，Java 和 Python 中将键插入 B 树的工作示例。

在 B 树上插入元素包括两个事件：搜索适当的节点来插入元素，以及拆分节点。如有必要，插入操作始终从下往上进行。

让我们在下面了解这些事件。

插入操作

  1. 如果树为空，请分配一个根节点并插入键。
  2. 更新节点中允许的键数。
  3. 搜索适当的节点以进行插入。
  4. 如果节点已满，请执行以下步骤。
  5. 按递增顺序插入元素。
  6. 现在，有一些元素超出了其限制。 因此，将中位数拆分。
  7. 向上推中键，将左键作为左子代，将右键作为右子代。
  8. 如果节点未满，请执行以下步骤。
  9. 按升序插入节点。

插入示例

让我们通过以下插图了解插入操作。

要插入的元素是 8、9、10、11、15、16、17、18、20、23。

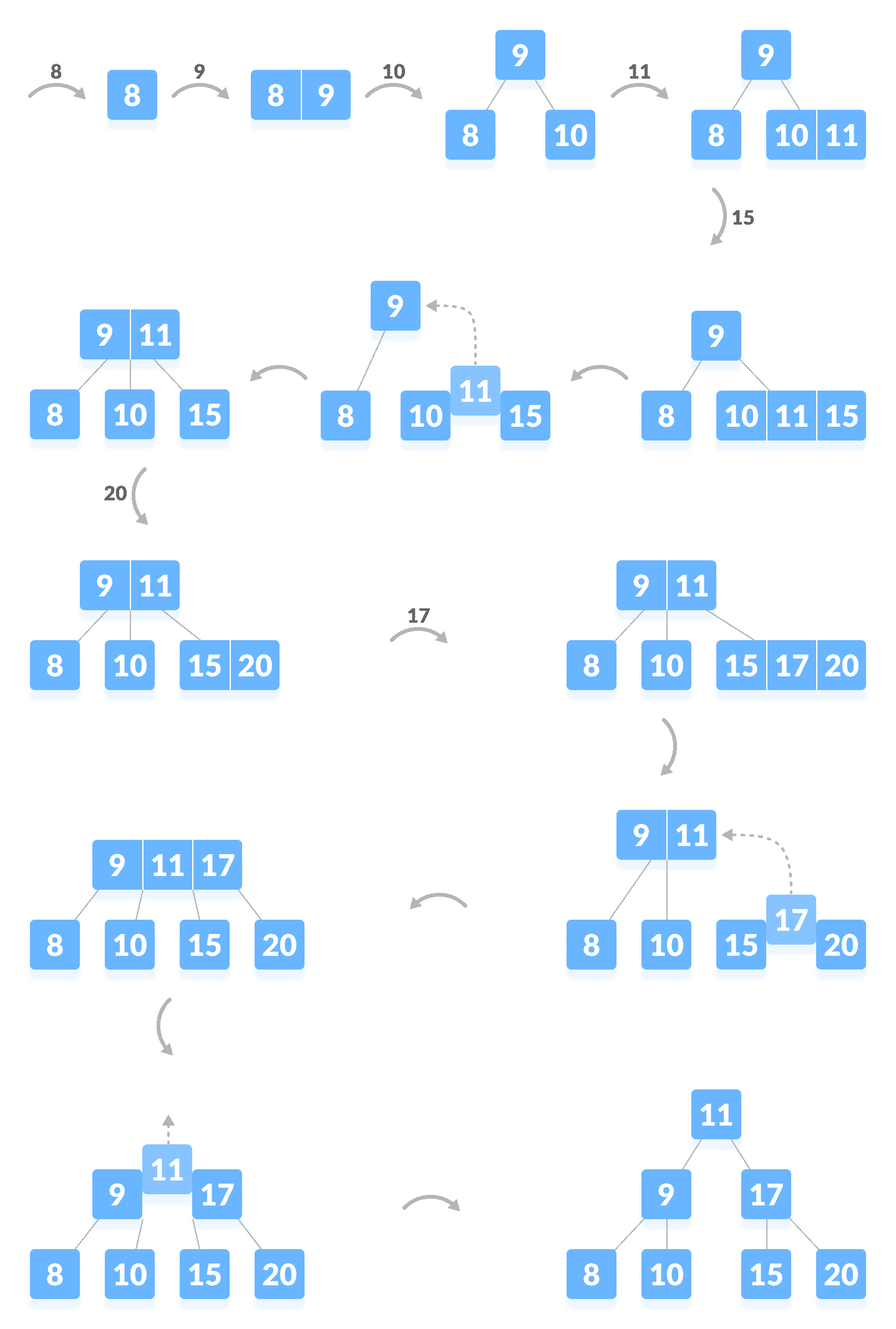
插入 B 树 - 图1

将元素插入 B 树

元素插入算法

  1. BreeInsertion(T, k)
  2. r  root[T]
  3. if n[r] = 2t - 1
  4.     s = AllocateNode()
  5.     root[T] = s
  6.     leaf[s] = FALSE
  7.     n[s] <- 0
  8.     c1[s] <- r
  9.     BtreeSplitChild(s, 1, r)
  10.     BtreeInsertNonFull(s, k)
  11. else BtreeInsertNonFull(r, k)
  12. BtreeInsertNonFull(x, k)
  13. i = n[x]
  14. if leaf[x]
  15.     while i ≥ 1 and k < keyi[x]
  16.         keyi+1 [x] = keyi[x]
  17.         i = i - 1
  18.     keyi+1[x] = k
  19.     n[x] = n[x] + 1
  20. else while i ≥ 1 and k < keyi[x]
  21.         i = i - 1
  22.     i = i + 1
  23.     if n[ci[x]] == 2t - 1
  24.         BtreeSplitChild(x, i, ci[x])
  25.         if k &rt; keyi[x]
  26.             i = i + 1
  27.     BtreeInsertNonFull(ci[x], k)
  28. BtreeSplitChild(x, i)
  29. BtreeSplitChild(x, i, y)
  30. z = AllocateNode()
  31. leaf[z] = leaf[y]
  32. n[z] = t - 1
  33. for j = 1 to t - 1
  34.     keyj[z] = keyj+t[y]
  35. if not leaf [y]
  36.     for j = 1 to t
  37.         cj[z] = cj + t[y]
  38. n[y] = t - 1
  39. for j = n[x] + 1 to i + 1
  40.     cj+1[x] = cj[x]
  41. ci+1[x] = z
  42. for j = n[x] to i
  43.     keyj+1[x] = keyj[x]
  44. keyi[x] = keyt[y]
  45. n[x] = n[x] + 1

Python，Java 和 C/C++ 示例

  1. # Inserting a key on a B-tree in Python
  3. # Create a node
  4. class BTreeNode:
  5.     def __init__(self, leaf=False):
  6.         self.leaf = leaf
  7.         self.keys = []
  8.         self.child = []
  10. # Tree
  11. class BTree:
  12.     def __init__(self, t):
  13.         self.root = BTreeNode(True)
  14.         self.t = t
  16.     # Insert node
  17.     def insert(self, k):
  18.         root = self.root
  19.         if len(root.keys) == (2 * self.t) - 1:
  20.             temp = BTreeNode()
  21.             self.root = temp
  22.             temp.child.insert(0, root)
  23.             self.split_child(temp, 0)
  24.             self.insert_non_full(temp, k)
  25.         else:
  26.             self.insert_non_full(root, k)
  28.     # Insert nonfull
  29.     def insert_non_full(self, x, k):
  30.         i = len(x.keys) - 1
  31.         if x.leaf:
  32.             x.keys.append((None, None))
  33.             while i >= 0 and k[0] < x.keys[i][0]:
  34.                 x.keys[i + 1] = x.keys[i]
  35.                 i -= 1
  36.             x.keys[i + 1] = k
  37.         else:
  38.             while i >= 0 and k[0] < x.keys[i][0]:
  39.                 i -= 1
  40.             i += 1
  41.             if len(x.child[i].keys) == (2 * self.t) - 1:
  42.                 self.split_child(x, i)
  43.                 if k[0] > x.keys[i][0]:
  44.                     i += 1
  45.             self.insert_non_full(x.child[i], k)
  47.     # Split the child
  48.     def split_child(self, x, i):
  49.         t = self.t
  50.         y = x.child[i]
  51.         z = BTreeNode(y.leaf)
  52.         x.child.insert(i + 1, z)
  53.         x.keys.insert(i, y.keys[t - 1])
  54.         z.keys = y.keys[t: (2 * t) - 1]
  55.         y.keys = y.keys[0: t - 1]
  56.         if not y.leaf:
  57.             z.child = y.child[t: 2 * t]
  58.             y.child = y.child[0: t - 1]
  60.     # Print the tree
  61.     def print_tree(self, x, l=0):
  62.         print("Level ", l, " ", len(x.keys), end=":")
  63.         for i in x.keys:
  64.             print(i, end=" ")
  65.         print()
  66.         l += 1
  67.         if len(x.child) > 0:
  68.             for i in x.child:
  69.                 self.print_tree(i, l)
  71. def main():
  72.     B = BTree(3)
  74.     for i in range(10):
  75.         B.insert((i, 2 * i))
  77.     B.print_tree(B.root)
  79. if __name__ == '__main__':
  80.     main()
  1. // Inserting a key on a B-tree in Java 
  3. public class BTree {
  5.   private int T;
  7.   // Node Creation
  8.   public class Node {
  9.     int n;
  10.     int key[] = new int[2 * T - 1];
  11.     Node child[] = new Node[2 * T];
  12.     boolean leaf = true;
  14.     public int Find(int k) {
  15.       for (int i = 0; i < this.n; i++) {
  16.         if (this.key[i] == k) {
  17.           return i;
  18.         }
  19.       }
  20.       return -1;
  21.     };
  22.   }
  24.   public BTree(int t) {
  25.     T = t;
  26.     root = new Node();
  27.     root.n = 0;
  28.     root.leaf = true;
  29.   }
  31.   private Node root;
  33.   // split
  34.   private void split(Node x, int pos, Node y) {
  35.     Node z = new Node();
  36.     z.leaf = y.leaf;
  37.     z.n = T - 1;
  38.     for (int j = 0; j < T - 1; j++) {
  39.       z.key[j] = y.key[j + T];
  40.     }
  41.     if (!y.leaf) {
  42.       for (int j = 0; j < T; j++) {
  43.         z.child[j] = y.child[j + T];
  44.       }
  45.     }
  46.     y.n = T - 1;
  47.     for (int j = x.n; j >= pos + 1; j--) {
  48.       x.child[j + 1] = x.child[j];
  49.     }
  50.     x.child[pos + 1] = z;
  52.     for (int j = x.n - 1; j >= pos; j--) {
  53.       x.key[j + 1] = x.key[j];
  54.     }
  55.     x.key[pos] = y.key[T - 1];
  56.     x.n = x.n + 1;
  57.   }
  59.   // insert key
  60.   public void insert(final int key) {
  61.     Node r = root;
  62.     if (r.n == 2 * T - 1) {
  63.       Node s = new Node();
  64.       root = s;
  65.       s.leaf = false;
  66.       s.n = 0;
  67.       s.child[0] = r;
  68.       split(s, 0, r);
  69.       _insert(s, key);
  70.     } else {
  71.       _insert(r, key);
  72.     }
  73.   }
  75.   // insert node
  76.   final private void _insert(Node x, int k) {
  78.     if (x.leaf) {
  79.       int i = 0;
  80.       for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
  81.         x.key[i + 1] = x.key[i];
  82.       }
  83.       x.key[i + 1] = k;
  84.       x.n = x.n + 1;
  85.     } else {
  86.       int i = 0;
  87.       for (i = x.n - 1; i >= 0 && k < x.key[i]; i--) {
  88.       }
  89.       ;
  90.       i++;
  91.       Node tmp = x.child[i];
  92.       if (tmp.n == 2 * T - 1) {
  93.         split(x, i, tmp);
  94.         if (k > x.key[i]) {
  95.           i++;
  96.         }
  97.       }
  98.       _insert(x.child[i], k);
  99.     }
  101.   }
  103.   public void display() {
  104.     display(root);
  105.   }
  107.   // Display the tree
  108.   private void display(Node x) {
  109.     assert (x == null);
  110.     for (int i = 0; i < x.n; i++) {
  111.       System.out.print(x.key[i] + " ");
  112.     }
  113.     if (!x.leaf) {
  114.       for (int i = 0; i < x.n + 1; i++) {
  115.         display(x.child[i]);
  116.       }
  117.     }
  118.   }
  120.   public static void main(String[] args) {
  121.     BTree b = new BTree(3);
  122.     b.insert(8);
  123.     b.insert(9);
  124.     b.insert(10);
  125.     b.insert(11);
  126.     b.insert(15);
  127.     b.insert(20);
  128.     b.insert(17);
  130.     b.display();
  131.   }
  132. }
  1. // insertioning a key on a B-tree in C
  3. #include <stdio.h>
  4. #include <stdlib.h>
  6. #define MAX 3
  7. #define MIN 2
  9. struct btreeNode {
  10.   int item[MAX + 1], count;
  11.   struct btreeNode *link[MAX + 1];
  12. };
  14. struct btreeNode *root;
  16. // Node creation
  17. struct btreeNode *createNode(int item, struct btreeNode *child) {
  18.   struct btreeNode *newNode;
  19.   newNode = (struct btreeNode *)malloc(sizeof(struct btreeNode));
  20.   newNode->item[1] = item;
  21.   newNode->count = 1;
  22.   newNode->link[0] = root;
  23.   newNode->link[1] = child;
  24.   return newNode;
  25. }
  27. // Insert
  28. void insertValue(int item, int pos, struct btreeNode *node,
  29.           struct btreeNode *child) {
  30.   int j = node->count;
  31.   while (j > pos) {
  32.     node->item[j + 1] = node->item[j];
  33.     node->link[j + 1] = node->link[j];
  34.     j--;
  35.   }
  36.   node->item[j + 1] = item;
  37.   node->link[j + 1] = child;
  38.   node->count++;
  39. }
  41. // Split node
  42. void splitNode(int item, int *pval, int pos, struct btreeNode *node,
  43.          struct btreeNode *child, struct btreeNode **newNode) {
  44.   int median, j;
  46.   if (pos > MIN)
  47.     median = MIN + 1;
  48.   else
  49.     median = MIN;
  51.   *newNode = (struct btreeNode *)malloc(sizeof(struct btreeNode));
  52.   j = median + 1;
  53.   while (j <= MAX) {
  54.     (*newNode)->item[j - median] = node->item[j];
  55.     (*newNode)->link[j - median] = node->link[j];
  56.     j++;
  57.   }
  58.   node->count = median;
  59.   (*newNode)->count = MAX - median;
  61.   if (pos <= MIN) {
  62.     insertValue(item, pos, node, child);
  63.   } else {
  64.     insertValue(item, pos - median, *newNode, child);
  65.   }
  66.   *pval = node->item[node->count];
  67.   (*newNode)->link[0] = node->link[node->count];
  68.   node->count--;
  69. }
  71. // Set the value of node
  72. int setNodeValue(int item, int *pval,
  73.            struct btreeNode *node, struct btreeNode **child) {
  74.   int pos;
  75.   if (!node) {
  76.     *pval = item;
  77.     *child = NULL;
  78.     return 1;
  79.   }
  81.   if (item < node->item[1]) {
  82.     pos = 0;
  83.   } else {
  84.     for (pos = node->count;
  85.        (item < node->item[pos] && pos > 1); pos--)
  86.       ;
  87.     if (item == node->item[pos]) {
  88.       printf("Duplicates not allowed\n");
  89.       return 0;
  90.     }
  91.   }
  92.   if (setNodeValue(item, pval, node->link[pos], child)) {
  93.     if (node->count < MAX) {
  94.       insertValue(*pval, pos, node, *child);
  95.     } else {
  96.       splitNode(*pval, pval, pos, node, *child, child);
  97.       return 1;
  98.     }
  99.   }
  100.   return 0;
  101. }
  103. // Insert the value
  104. void insertion(int item) {
  105.   int flag, i;
  106.   struct btreeNode *child;
  108.   flag = setNodeValue(item, &i, root, &child);
  109.   if (flag)
  110.     root = createNode(i, child);
  111. }
  113. // Copy the successor
  114. void copySuccessor(struct btreeNode *myNode, int pos) {
  115.   struct btreeNode *dummy;
  116.   dummy = myNode->link[pos];
  118.   for (; dummy->link[0] != NULL;)
  119.     dummy = dummy->link[0];
  120.   myNode->item[pos] = dummy->item[1];
  121. }
  123. // Do rightshift
  124. void rightShift(struct btreeNode *myNode, int pos) {
  125.   struct btreeNode *x = myNode->link[pos];
  126.   int j = x->count;
  128.   while (j > 0) {
  129.     x->item[j + 1] = x->item[j];
  130.     x->link[j + 1] = x->link[j];
  131.   }
  132.   x->item[1] = myNode->item[pos];
  133.   x->link[1] = x->link[0];
  134.   x->count++;
  136.   x = myNode->link[pos - 1];
  137.   myNode->item[pos] = x->item[x->count];
  138.   myNode->link[pos] = x->link[x->count];
  139.   x->count--;
  140.   return;
  141. }
  143. // Do leftshift
  144. void leftShift(struct btreeNode *myNode, int pos) {
  145.   int j = 1;
  146.   struct btreeNode *x = myNode->link[pos - 1];
  148.   x->count++;
  149.   x->item[x->count] = myNode->item[pos];
  150.   x->link[x->count] = myNode->link[pos]->link[0];
  152.   x = myNode->link[pos];
  153.   myNode->item[pos] = x->item[1];
  154.   x->link[0] = x->link[1];
  155.   x->count--;
  157.   while (j <= x->count) {
  158.     x->item[j] = x->item[j + 1];
  159.     x->link[j] = x->link[j + 1];
  160.     j++;
  161.   }
  162.   return;
  163. }
  165. // Merge the nodes
  166. void mergeNodes(struct btreeNode *myNode, int pos) {
  167.   int j = 1;
  168.   struct btreeNode *x1 = myNode->link[pos], *x2 = myNode->link[pos - 1];
  170.   x2->count++;
  171.   x2->item[x2->count] = myNode->item[pos];
  172.   x2->link[x2->count] = myNode->link[0];
  174.   while (j <= x1->count) {
  175.     x2->count++;
  176.     x2->item[x2->count] = x1->item[j];
  177.     x2->link[x2->count] = x1->link[j];
  178.     j++;
  179.   }
  181.   j = pos;
  182.   while (j < myNode->count) {
  183.     myNode->item[j] = myNode->item[j + 1];
  184.     myNode->link[j] = myNode->link[j + 1];
  185.     j++;
  186.   }
  187.   myNode->count--;
  188.   free(x1);
  189. }
  191. // Adjust the node
  192. void adjustNode(struct btreeNode *myNode, int pos) {
  193.   if (!pos) {
  194.     if (myNode->link[1]->count > MIN) {
  195.       leftShift(myNode, 1);
  196.     } else {
  197.       mergeNodes(myNode, 1);
  198.     }
  199.   } else {
  200.     if (myNode->count != pos) {
  201.       if (myNode->link[pos - 1]->count > MIN) {
  202.         rightShift(myNode, pos);
  203.       } else {
  204.         if (myNode->link[pos + 1]->count > MIN) {
  205.           leftShift(myNode, pos + 1);
  206.         } else {
  207.           mergeNodes(myNode, pos);
  208.         }
  209.       }
  210.     } else {
  211.       if (myNode->link[pos - 1]->count > MIN)
  212.         rightShift(myNode, pos);
  213.       else
  214.         mergeNodes(myNode, pos);
  215.     }
  216.   }
  217. }
  219. // Traverse the tree
  220. void traversal(struct btreeNode *myNode) {
  221.   int i;
  222.   if (myNode) {
  223.     for (i = 0; i < myNode->count; i++) {
  224.       traversal(myNode->link[i]);
  225.       printf("%d ", myNode->item[i + 1]);
  226.     }
  227.     traversal(myNode->link[i]);
  228.   }
  229. }
  231. int main() {
  232.   int item, ch;
  234.   insertion(8);
  235.   insertion(9);
  236.   insertion(10);
  237.   insertion(11);
  238.   insertion(15);
  239.   insertion(16);
  240.   insertion(17);
  241.   insertion(18);
  242.   insertion(20);
  243.   insertion(23);
  245.   traversal(root);
  246. }
// Inserting a key on a B-tree in C++

#include <iostream>
using namespace std;

class Node {
  int *keys;
  int t;
  Node **C;
  int n;
  bool leaf;

   public:
  Node(int _t, bool _leaf);

  void insertNonFull(int k);
  void splitChild(int i, Node *y);
  void traverse();

  friend class BTree;
};

class BTree {
  Node *root;
  int t;

   public:
  BTree(int _t) {
    root = NULL;
    t = _t;
  }

  void traverse() {
    if (root != NULL)
      root->traverse();
  }

  void insert(int k);
};

Node::Node(int t1, bool leaf1) {
  t = t1;
  leaf = leaf1;

  keys = new int[2 * t - 1];
  C = new Node *[2 * t];

  n = 0;
}

// Traverse the nodes
void Node::traverse() {
  int i;
  for (i = 0; i < n; i++) {
    if (leaf == false)
      C[i]->traverse();
    cout << " " << keys[i];
  }

  if (leaf == false)
    C[i]->traverse();
}

// Insert the node
void BTree::insert(int k) {
  if (root == NULL) {
    root = new Node(t, true);
    root->keys[0] = k;
    root->n = 1;
  } else {
    if (root->n == 2 * t - 1) {
      Node *s = new Node(t, false);

      s->C[0] = root;

      s->splitChild(0, root);

      int i = 0;
      if (s->keys[0] < k)
        i++;
      s->C[i]->insertNonFull(k);

      root = s;
    } else
      root->insertNonFull(k);
  }
}

// Insert non full condition
void Node::insertNonFull(int k) {
  int i = n - 1;

  if (leaf == true) {
    while (i >= 0 && keys[i] > k) {
      keys[i + 1] = keys[i];
      i--;
    }

    keys[i + 1] = k;
    n = n + 1;
  } else {
    while (i >= 0 && keys[i] > k)
      i--;

    if (C[i + 1]->n == 2 * t - 1) {
      splitChild(i + 1, C[i + 1]);

      if (keys[i + 1] < k)
        i++;
    }
    C[i + 1]->insertNonFull(k);
  }
}

// split the child
void Node::splitChild(int i, Node *y) {
  Node *z = new Node(y->t, y->leaf);
  z->n = t - 1;

  for (int j = 0; j < t - 1; j++)
    z->keys[j] = y->keys[j + t];

  if (y->leaf == false) {
    for (int j = 0; j < t; j++)
      z->C[j] = y->C[j + t];
  }

  y->n = t - 1;
  for (int j = n; j >= i + 1; j--)
    C[j + 1] = C[j];

  C[i + 1] = z;

  for (int j = n - 1; j >= i; j--)
    keys[j + 1] = keys[j];

  keys[i] = y->keys[t - 1];
  n = n + 1;
}

int main() {
  BTree t(3);
  t.insert(8);
  t.insert(9);
  t.insert(10);
  t.insert(11);
  t.insert(15);
  t.insert(16);
  t.insert(17);
  t.insert(18);
  t.insert(20);
  t.insert(23);

  cout << "The B-tree is: ";
  t.traverse();
}