原文： https://www.programiz.com/dsa/quick-sort

在本教程中，您将学习快速排序的工作原理。 此外，您还将找到 C，C++ Python 和 Java 中快速排序的工作示例。

快速排序是一种基于分治方法的算法，其中将数组拆分为子数组，然后递归调用这些子数组以对元素进行排序。

快速排序如何工作？

  1. 从数组中选择枢轴元素。 您可以从数组中选择任何元素作为枢轴元素。
    在这里，我们将数组的最右边（即最后一个元素）作为枢轴元素。
    快速排序算法 - 图1
    选择枢轴元素

  2. 小于枢轴元素的元素放在左侧，大于枢轴元素的元素放在右侧。
    快速排序算法 - 图2
    将所有较小的元素放在枢轴元素
    的左侧，将较大的元素放在右侧。

    1. 指针固定在枢轴元件上。 将枢轴元素与从第一个索引开始的元素进行比较。 如果达到大于枢轴元素的元素，则为该元素设置第二个指针。

    2. 现在，将枢轴元素与其他元素（第三个指针）进行比较。 如果到达的元素小于枢轴元素，则将较小的元素替换为较早找到的较大的元素。
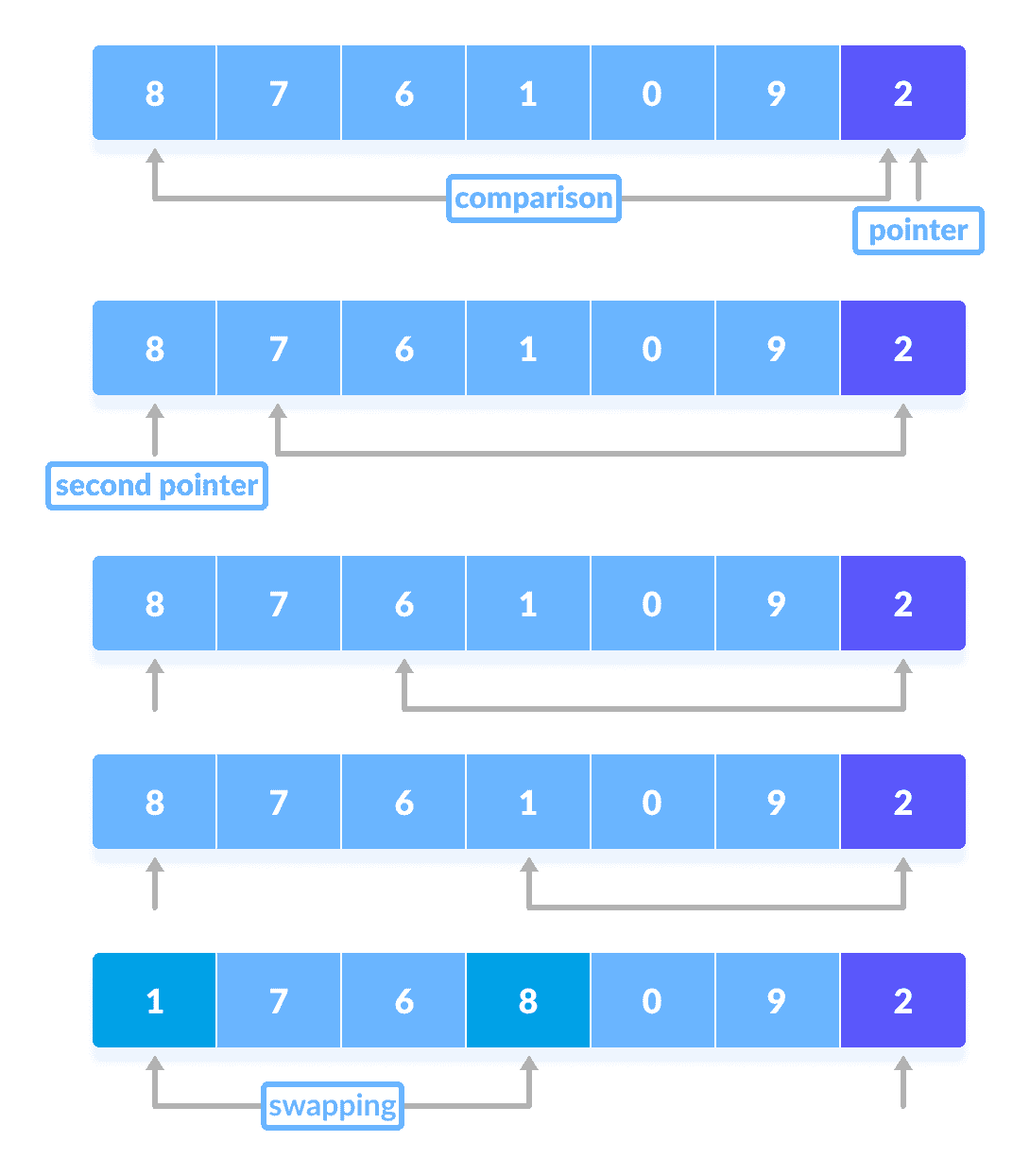
      快速排序算法 - 图3
      枢轴元素与其他元素的比较

    3. 该过程一直进行到到达倒数第二个元素为止。
      最后，将枢轴元素与第二个指针交换。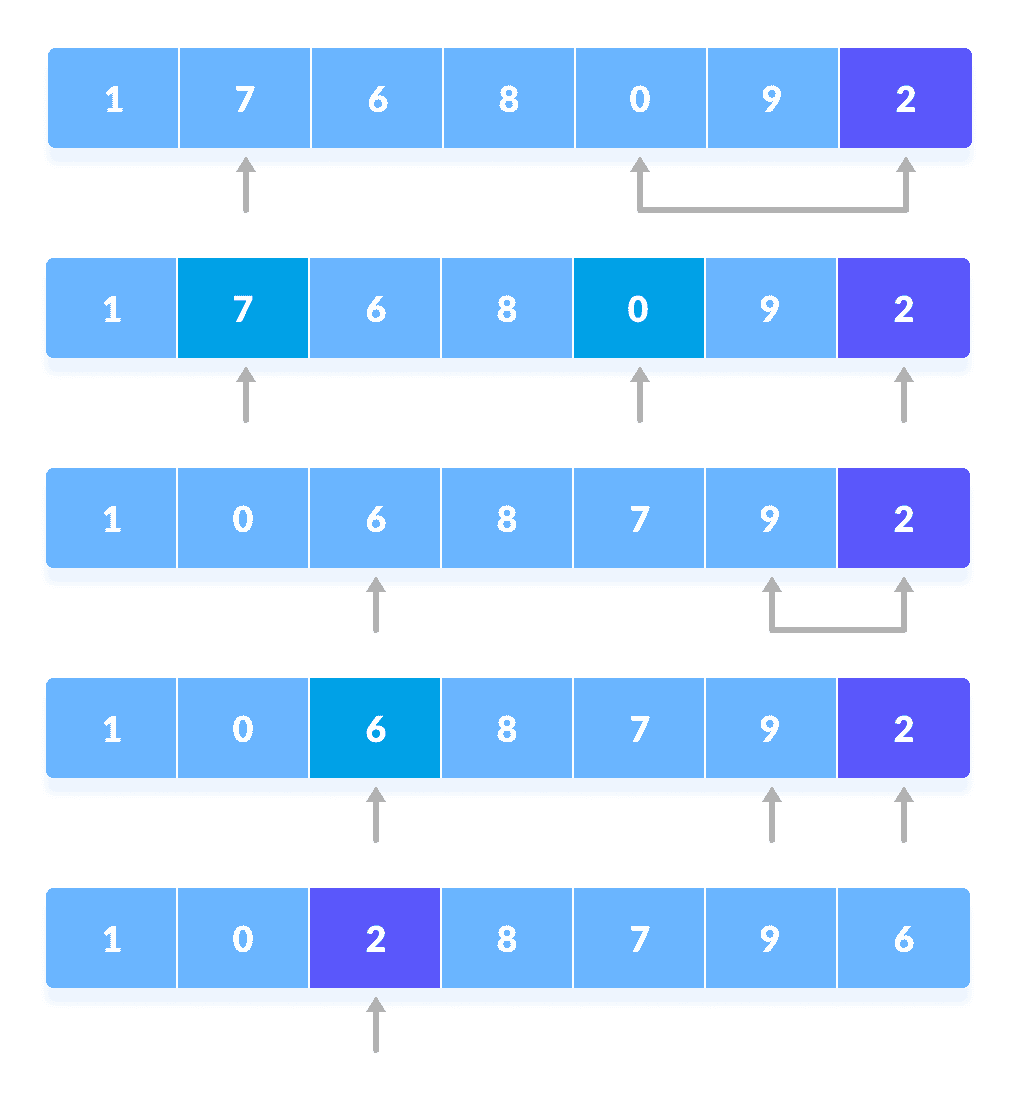
      快速排序算法 - 图4
      与第二个指针
      交换枢轴元素

  3. 再次分别为左子部分和右子部分选择了枢轴元素。 在这些子部件中，枢轴元件放置在正确的位置。 然后，重复步骤 2。
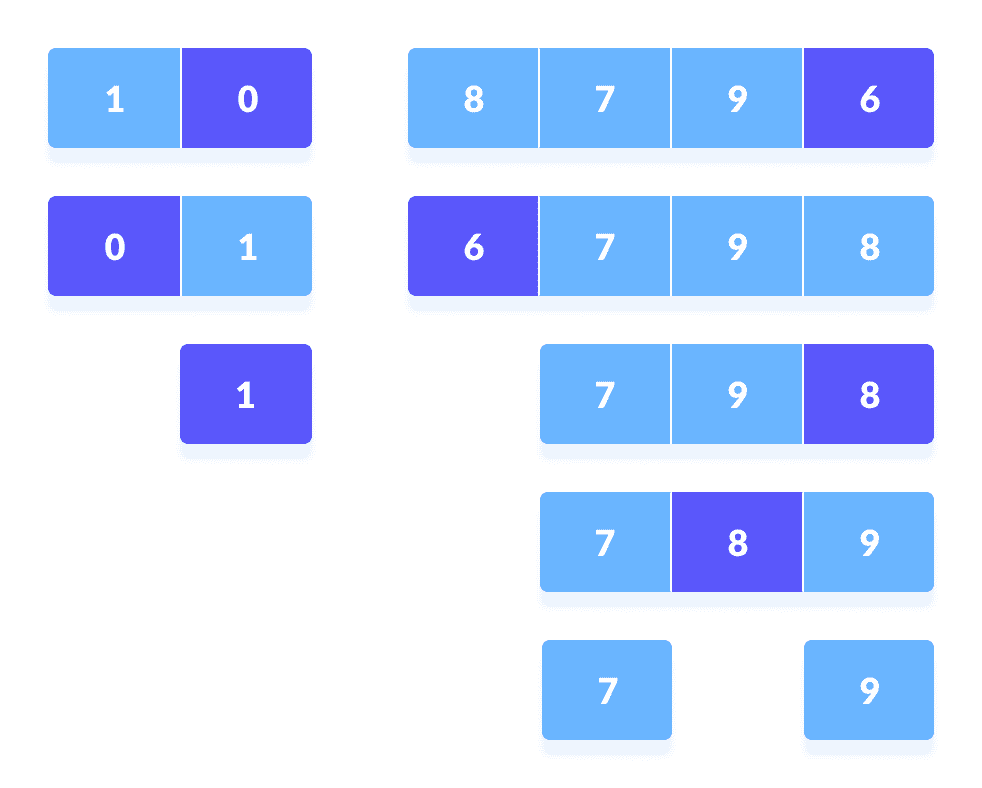
    快速排序算法 - 图5
    在每一半中选择枢轴元素，然后使用递归
    将其放置在正确的位置

  4. 将子部分再次划分为较小的子部分，直到每个子部分由单个元素形成。

  5. 至此，该数组已经排序。

快速排序使用递归对子部分进行排序。

在分治法的基础上，快速排序算法可以解释为：

  • 划分
    将数组划分为以枢轴为分割点的子部分。 小于枢轴的元素放置在枢轴的左侧，大于枢轴的元素放置在右侧。
  • 解决
    左子部分和右子部分再次通过选择枢轴元素进行划分。 这可以通过将子部分递归传递到算法中来实现。
  • 合并
    此步骤在快速排序中不起作用。 该数组已在解决步骤的末尾排序。

您可以在以下插图的帮助下了解快速排序的工作方式。

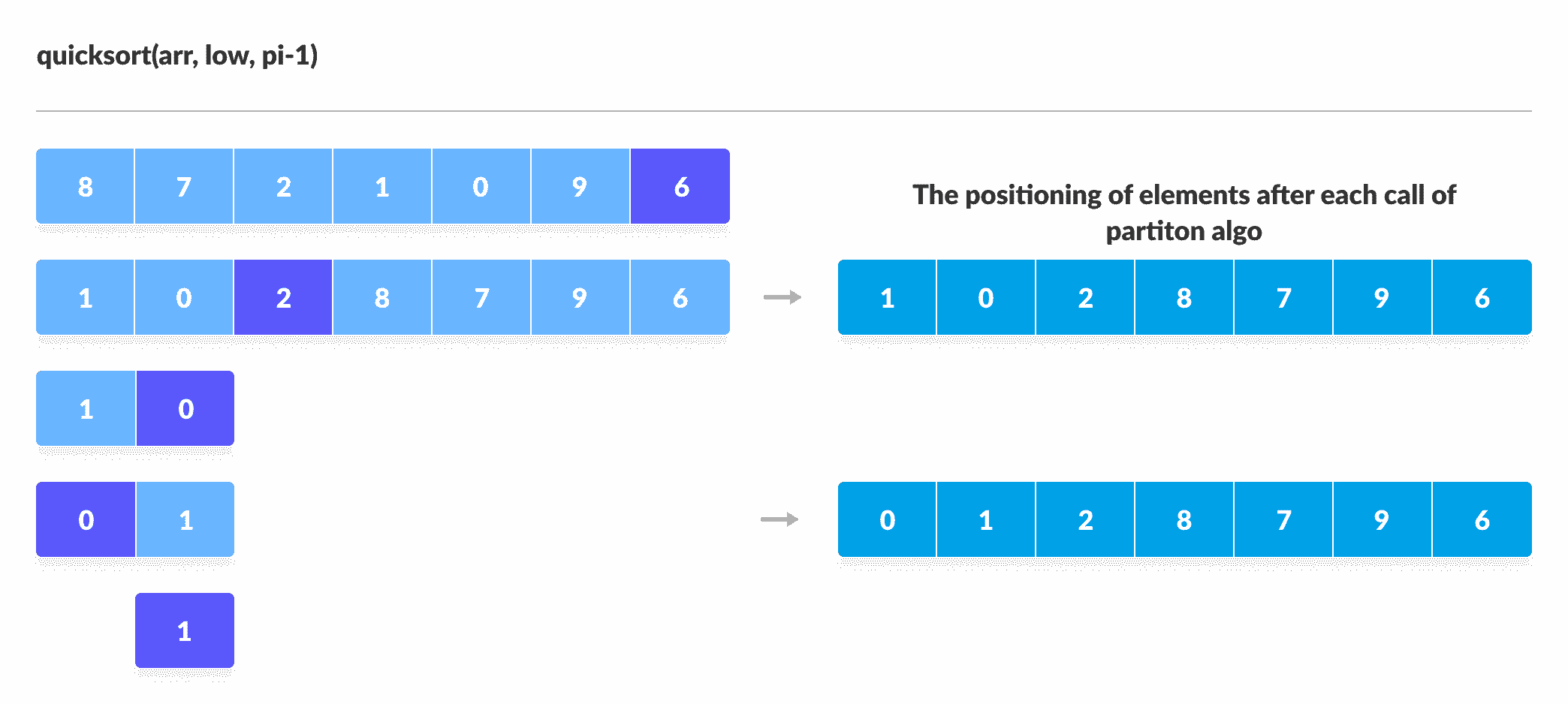
快速排序算法 - 图6

使用递归对枢轴左侧的元素进行排序

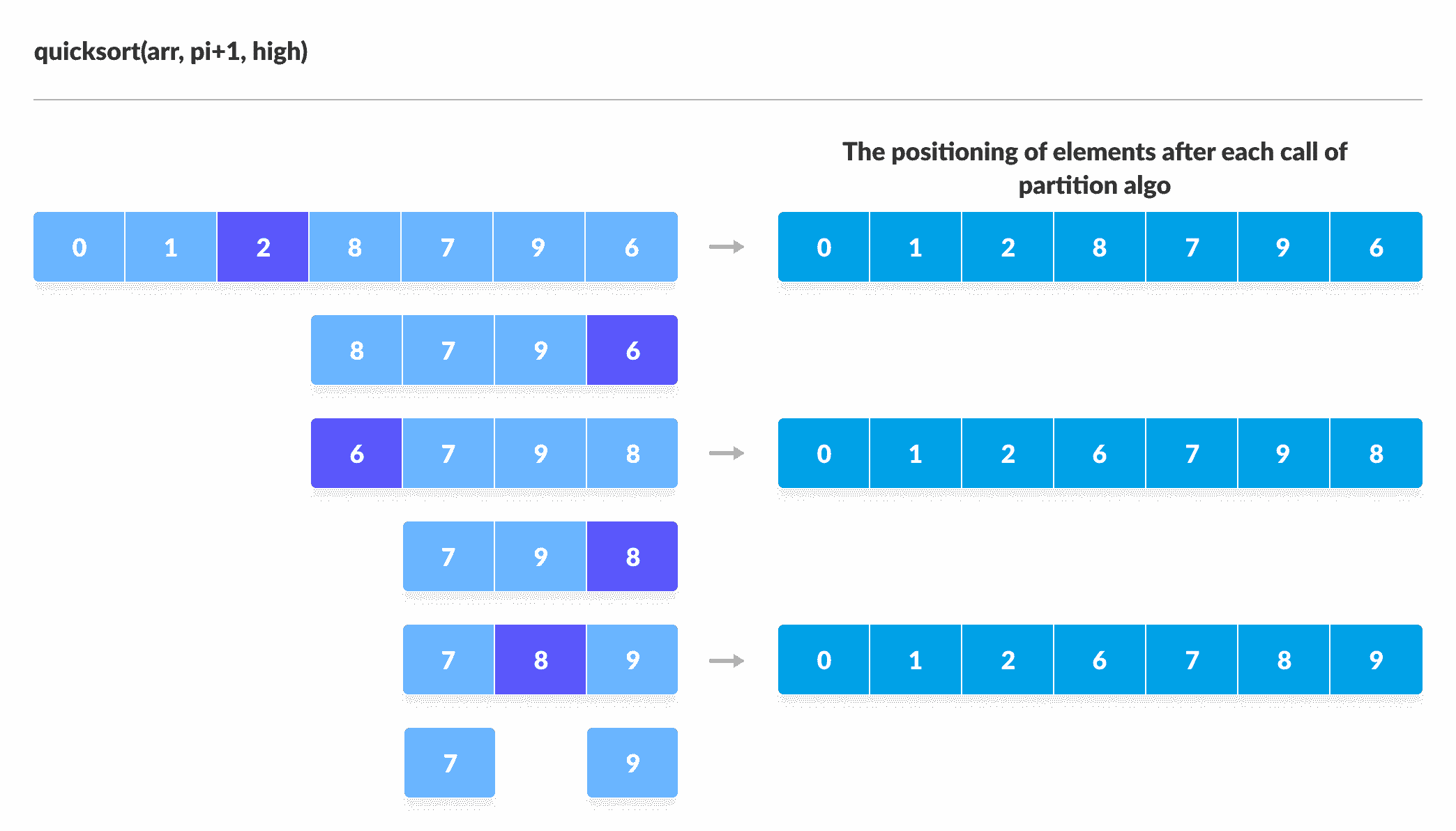
快速排序算法 - 图7

使用递归对枢轴右侧的元素进行排序

快速排序算法

  1. quickSort(array, leftmostIndex, rightmostIndex)
  2.   if (leftmostIndex < rightmostIndex)
  3.     pivotIndex <- partition(array,leftmostIndex, rightmostIndex)
  4.     quickSort(array, leftmostIndex, pivotIndex)
  5.     quickSort(array, pivotIndex + 1, rightmostIndex)
  7. partition(array, leftmostIndex, rightmostIndex)
  8.   set rightmostIndex as pivotIndex
  9.   storeIndex <- leftmostIndex - 1
  10.   for i <- leftmostIndex + 1 to rightmostIndex
  11.   if element[i] < pivotElement
  12.     swap element[i] and element[storeIndex]
  13.     storeIndex++
  14.   swap pivotElement and element[storeIndex+1]
  15. return storeIndex + 1

Python，Java 和 C/C++ 示例

# Quick sort in Python

# Function to partition the array on the basis of pivot element
def partition(array, low, high):

    # Select the pivot element
    pivot = array[high]
    i = low - 1

    # Put the elements smaller than pivot on the left and greater 
    #than pivot on the right of pivot
    for j in range(low, high):
        if array[j] <= pivot:
            i = i + 1
            (array[i], array[j]) = (array[j], array[i])

    (array[i + 1], array[high]) = (array[high], array[i + 1])

    return i + 1

def quickSort(array, low, high):
    if low < high:

        # Select pivot position and put all the elements smaller 
        # than pivot on left and greater than pivot on right
        pi = partition(array, low, high)

        # Sort the elements on the left of pivot
        quickSort(array, low, pi - 1)

        # Sort the elements on the right of pivot
        quickSort(array, pi + 1, high)

data = [8, 7, 2, 1, 0, 9, 6]
size = len(data)
quickSort(data, 0, size - 1)
print('Sorted Array in Ascending Order:')
print(data)

// Quick sort in Java

import java.util.Arrays;

class QuickSort {

  // Function to partition the array on the basis of pivot element
  int partition(int array[], int low, int high) {

    // Select the pivot element
    int pivot = array[high];
    int i = (low - 1);

    // Put the elements smaller than pivot on the left and 
    // greater than pivot on the right of pivot
    for (int j = low; j < high; j++) {
      if (array[j] <= pivot) {
        i++;
        int temp = array[i];
        array[i] = array[j];
        array[j] = temp;
      }
    }
    int temp = array[i + 1];
    array[i + 1] = array[high];
    array[high] = temp;
    return (i + 1);
  }

  void quickSort(int array[], int low, int high) {
    if (low < high) {

      // Select pivot position and put all the elements smaller 
      // than pivot on left and greater than pivot on right
      int pi = partition(array, low, high);

      // Sort the elements on the left of pivot
      quickSort(array, low, pi - 1);

      // Sort the elements on the right of pivot
      quickSort(array, pi + 1, high);
    }
  }

  // Driver code
  public static void main(String args[]) {
    int[] data = { 8, 7, 2, 1, 0, 9, 6 };
    int size = data.length;
    QuickSort qs = new QuickSort();
    qs.quickSort(data, 0, size - 1);
    System.out.println("Sorted Array in Ascending Order: ");
    System.out.println(Arrays.toString(data));
  }
}

// Quick sort in C

#include <stdio.h>

// Function to swap position of elements
void swap(int *a, int *b) {
  int t = *a;
  *a = *b;
  *b = t;
}

// Function to partition the array on the basis of pivot element
int partition(int array[], int low, int high) {

  // Select the pivot element
  int pivot = array[high];
  int i = (low - 1);

  // Put the elements smaller than pivot on the left 
  // and greater than pivot on the right of pivot
  for (int j = low; j < high; j++) {
    if (array[j] <= pivot) {
      i++;
      swap(&array[i], &array[j]);
    }
  }

  swap(&array[i + 1], &array[high]);
  return (i + 1);
}

void quickSort(int array[], int low, int high) {
  if (low < high) {

    // Select pivot position and put all the elements smaller 
    // than pivot on left and greater than pivot on right
    int pi = partition(array, low, high);

    // Sort the elements on the left of pivot
    quickSort(array, low, pi - 1);

    // Sort the elements on the right of pivot
    quickSort(array, pi + 1, high);
  }
}

// Function to print eklements of an array
void printArray(int array[], int size) {
  for (int i = 0; i < size; ++i) {
    printf("%d  ", array[i]);
  }
  printf("\n");
}

// Driver code
int main() {
  int data[] = {8, 7, 2, 1, 0, 9, 6};
  int n = sizeof(data) / sizeof(data[0]);
  quickSort(data, 0, n - 1);
  printf("Sorted array in ascending order: \n");
  printArray(data, n);
}

// Quick sort in C++

#include <iostream>
using namespace std;

// Function to swap position of elements
void swap(int *a, int *b) {
  int t = *a;
  *a = *b;
  *b = t;
}

// Function to print eklements of an array
void printArray(int array[], int size) {
  int i;
  for (i = 0; i < size; i++)
    cout << array[i] << " ";
  cout << endl;
}

// Function to partition the array on the basis of pivot element
int partition(int array[], int low, int high) {
  // Select the pivot element
  int pivot = array[high];
  int i = (low - 1);

  // Put the elements smaller than pivot on the left 
  // and greater than pivot on the right of pivot
  for (int j = low; j < high; j++) {
    if (array[j] <= pivot) {
      i++;
      swap(&array[i], &array[j]);
    }
  }
  printArray(array, 7);
  cout << "........\n";
  swap(&array[i + 1], &array[high]);
  return (i + 1);
}

void quickSort(int array[], int low, int high) {
  if (low < high) {
    // Select pivot position and put all the elements smaller 
    // than pivot on left and greater than pivot on right
    int pi = partition(array, low, high);

    // Sort the elements on the left of pivot
    quickSort(array, low, pi - 1);

    // Sort the elements on the right of pivot
    quickSort(array, pi + 1, high);
  }
}

// Driver code
int main() {
  int data[] = {8, 7, 6, 1, 0, 9, 2};
  int n = sizeof(data) / sizeof(data[0]);
  quickSort(data, 0, n - 1);
  cout << "Sorted array in ascending order: \n";
  printArray(data, n);
}

快速排序的复杂度

时间复杂度

  • 最坏情况的复杂度【大 O】 ：O(n^2)
    当拾取的枢轴元素为最大或最小元素时，会发生这种情况。
    这种情况导致枢轴元素位于已排序数组的最末端的情况。 一个子数组始终为空，而另一个子数组包含n - 1元素。 因此，仅在此子数组上调用快速排序。
    但是，快速排序算法对于分散的数据透视表具有更好的性能。

  • 最佳情况复杂度【大 Ω】 ：O(n*log n)
    当枢轴元素始终是中间元素或靠近中间元素时，会发生这种情况。

  • 平均病例复杂度【大 θ】 ：O(n*log n)
    当不出现上述条件时发生。

空间复杂度

快速排序的空间复杂度为O(log n)。

快速排序应用

快速排序在以下情况下实现

  • 编程语言适合递归
  • 时间复杂度很重要
  • 空间复杂度很重要