平衡二叉树

原文： https://www.programiz.com/dsa/balanced-binary-tree

在本教程中，您将了解平衡的二叉树及其不同类型。 此外，您还将在 C，C++ ，Java 和 Python 中找到平衡二叉树的工作示例。

平衡二叉树（也称为高度平衡二叉树）定义为二叉树，其中任何节点的左和右子树的高度相差不超过 1。

要了解有关树/节点的高度的更多信息，请访问树数据结构。以下是高度平衡的二叉树的条件：

1. 任何节点的左和右子树之间的差异不超过一个
2. 左子树是平衡的
3. 右子树是平衡的

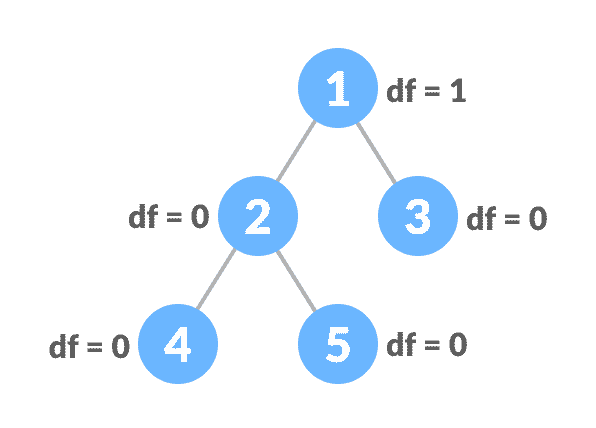
每个级别都有深度的平衡二叉树

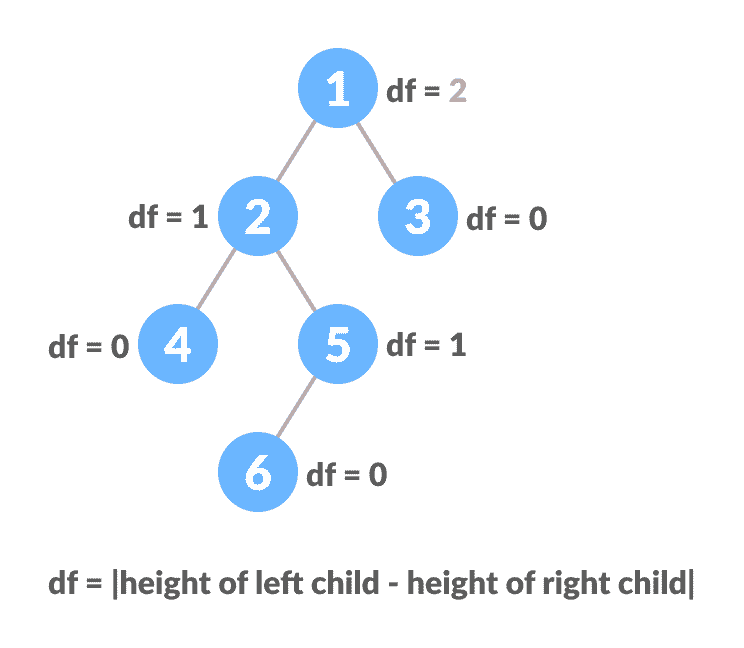
每个级别都有深度的不平衡二叉树

Python，Java 和 C/C++ 示例

以下代码用于检查树是否高度平衡。

# Checking if a binary tree is CalculateHeight balanced in Python
# CreateNode creation
class CreateNode:
    def __init__(self, item):
        self.item = item
        self.left = self.right = None
# Calculate height
class CalculateHeight:
    def __init__(self):
        self.CalculateHeight = 0
# Check height balance
def is_height_balanced(root, CalculateHeight):
    left_height = CalculateHeight()
    right_height = CalculateHeight()
    if root is None:
        return True
    l = is_height_balanced(root.left, left_height)
    r = is_height_balanced(root.right, right_height)
    CalculateHeight.CalculateHeight = max(
        left_height.CalculateHeight, right_height.CalculateHeight) + 1
    if abs(left_height.CalculateHeight - right_height.CalculateHeight) <= 1:
        return l and r
    return False
CalculateHeight = CalculateHeight()
root = CreateNode(1)
root.left = CreateNode(2)
root.right = CreateNode(3)
root.left.left = CreateNode(4)
root.left.right = CreateNode(5)
if is_height_balanced(root, CalculateHeight):
    print('The tree is balanced')
else:
    print('The tree is not balanced')

// Checking if a binary tree is height balanced in Java
// Node creation
class Node {
  int data;
  Node left, right;
  Node(int d) {
    data = d;
    left = right = null;
  }
}
// Calculate height
class Height {
  int height = 0;
}
class BinaryTree {
  Node root;
  // Check height balance
  boolean checkHeightBalance(Node root, Height height) {
    // Check for emptiness
    if (root == null) {
      height.height = 0;
      return true;
    }
    Height leftHeighteight = new Height(), rightHeighteight = new Height();
    boolean l = checkHeightBalance(root.left, leftHeighteight);
    boolean r = checkHeightBalance(root.right, rightHeighteight);
    int leftHeight = leftHeighteight.height, rightHeight = rightHeighteight.height;
    height.height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
    if ((leftHeight - rightHeight >= 2) || (rightHeight - leftHeight >= 2))
      return false;
    else
      return l && r;
  }
  public static void main(String args[]) {
    Height height = new Height();
    BinaryTree tree = new BinaryTree();
    tree.root = new Node(1);
    tree.root.left = new Node(2);
    tree.root.right = new Node(3);
    tree.root.left.left = new Node(4);
    tree.root.left.right = new Node(5);
    if (tree.checkHeightBalance(tree.root, height))
      System.out.println("The tree is balanced");
    else
      System.out.println("The tree is not balanced");
  }
}

// Checking if a binary tree is height balanced in C
#include <stdio.h>
#include <stdlib.h>
#define bool int
// Node creation
struct node {
  int item;
  struct node *left;
  struct node *right;
};
// Create a new node
struct node *newNode(int item) {
  struct node *node = (struct node *)malloc(sizeof(struct node));
  node->item = item;
  node->left = NULL;
  node->right = NULL;
  return (node);
}
// Check for height balance
bool checkHeightBalance(struct node *root, int *height) {
  // Check for emptiness
  int leftHeight = 0, rightHeight = 0;
  int l = 0, r = 0;
  if (root == NULL) {
    *height = 0;
    return 1;
  }
  l = checkHeightBalance(root->left, &leftHeight);
  r = checkHeightBalance(root->right, &rightHeight);
  *height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
  if ((leftHeight - rightHeight >= 2) || (rightHeight - leftHeight >= 2))
    return 0;
  else
    return l && r;
}
int main() {
  int height = 0;
  struct node *root = newNode(1);
  root->left = newNode(2);
  root->right = newNode(3);
  root->left->left = newNode(4);
  root->left->right = newNode(5);
  if (checkHeightBalance(root, &height))
    printf("The tree is balanced");
  else
    printf("The tree is not balanced");
}

// Checking if a binary tree is height balanced in C++
#include <iostream>
using namespace std;
#define bool int
class node {
   public:
  int item;
  node *left;
  node *right;
};
// Create anew node
node *newNode(int item) {
  node *Node = new node();
  Node->item = item;
  Node->left = NULL;
  Node->right = NULL;
  return (Node);
}
// Check height balance
bool checkHeightBalance(node *root, int *height) {
  // Check for emptiness
  int leftHeight = 0, rightHeight = 0;
  int l = 0, r = 0;
  if (root == NULL) {
    *height = 0;
    return 1;
  }
  l = checkHeightBalance(root->left, &leftHeight);
  r = checkHeightBalance(root->right, &rightHeight);
  *height = (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
  if ((leftHeight - rightHeight >= 2) || (rightHeight - leftHeight >= 2))
    return 0;
  else
    return l && r;
}
int main() {
  int height = 0;
  node *root = newNode(1);
  root->left = newNode(2);
  root->right = newNode(3);
  root->left->left = newNode(4);
  root->left->right = newNode(5);
  if (checkHeightBalance(root, &height))
    cout << "The tree is balanced";
  else
    cout << "The tree is not balanced";
}

平衡二叉树应用

• AVL 树
• 平衡的二叉搜索树