原文： https://www.programiz.com/dsa/shell-sort

在本教程中，您将学习 shell 排序的工作方式。 此外，您还将找到使用 C，C++ ，Java 和 Python 进行 shell 排序的工作示例。

Shell 排序是一种算法，该算法首先对彼此分开的元素进行排序，然后依次减小要排序的元素之间的间隔。 它是插入排序的通用版本。

在 Shell 排序中，将按特定间隔对元素进行排序。 元素之间的间隔根据使用的顺序逐渐减小。 shell 排序的性能取决于给定输入数组使用的序列类型。

使用的一些最佳顺序是：

  • Shell 的原始顺序：N/2 , N/4 , …, 1
  • Knuth 的增量：1, 4, 13, …, (3k – 1) / 2
  • Sedgewick 的增量：1, 8, 23, 77, 281, 1073, 4193, 16577...4j+1+ 3·2j+ 1
  • 希伯德的增幅：1, 3, 7, 15, 31, 63, 127, 255, 511…
  • Papernov & Stasevich 增量：1, 3, 5, 9, 17, 33, 65,...
  • 普拉特：1, 2, 3, 4, 6, 9, 8, 12, 18, 27, 16, 24, 36, 54, 81....

Shell 排序如何工作？

  1. 假设我们需要对以下数组进行排序。
    Shell 排序算法 - 图1
    初始数组

  2. 我们在算法中使用了外壳的原始序列(N/2, N/4, ...1)作为间隔。
    在第一个循环中，如果数组大小为N = 8，则比较N/2 = 4间隔的元素，如果顺序不对则交换它们。

    1. 将第 0 个元素与第 4 个元素进行比较。

    2. 如果第 0 个元素大于第 4 个，则首先将第 4 个元素存储在temp变量中，并将第 0 个元素（即更大的元素）存储在第 4 个位置和存储在temp中的元素存储在第 0 个位置。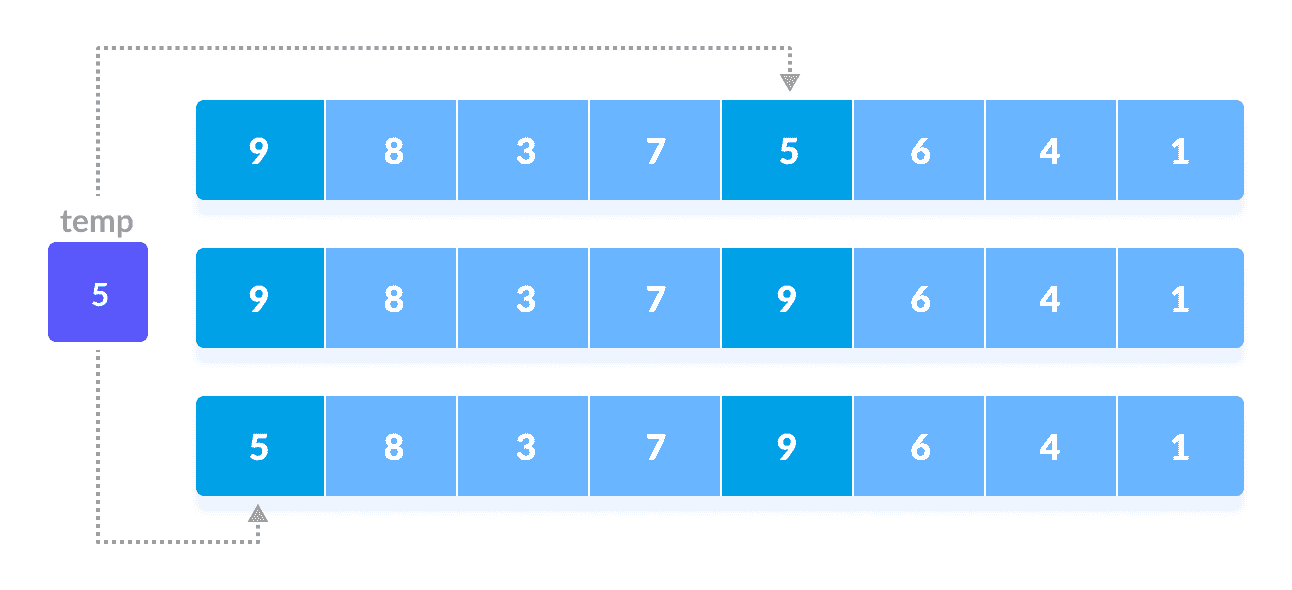
      Shell 排序算法 - 图2
      以n / 2的间隔重新排列元素。
      对于所有其余元素，此过程将继续进行。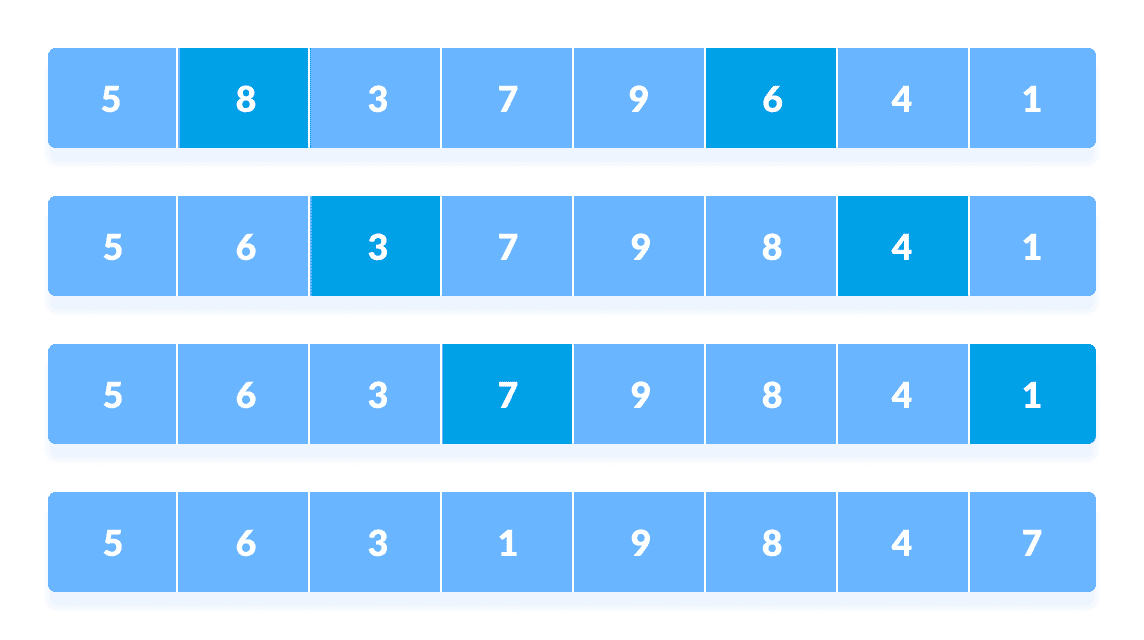
      Shell 排序算法 - 图3
      以n / 2间隔重新排列所有元素

  3. 在第二个循环中，采用N/4 = 8/4 = 2的间隔，并再次对位于这些间隔的元素进行排序。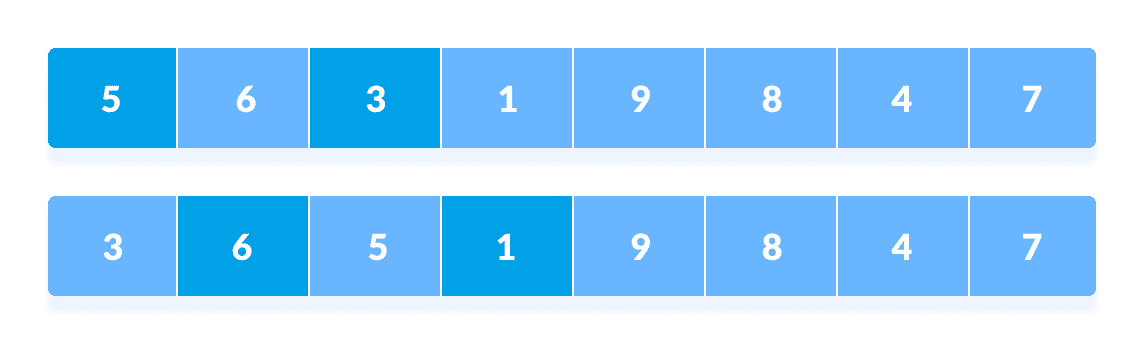
    Shell 排序算法 - 图4
    以n / 4的间隔重新排列元素
    此时，您可能会感到困惑。
    Shell 排序算法 - 图5
    比较当前间隔中数组中的所有元素。 比较第 4 个和第 2 个位置的元素。 还比较了第 2 个和第 0 个位置的元素。 比较当前间隔中数组中的所有元素。

  4. 其余元素的处理相同。
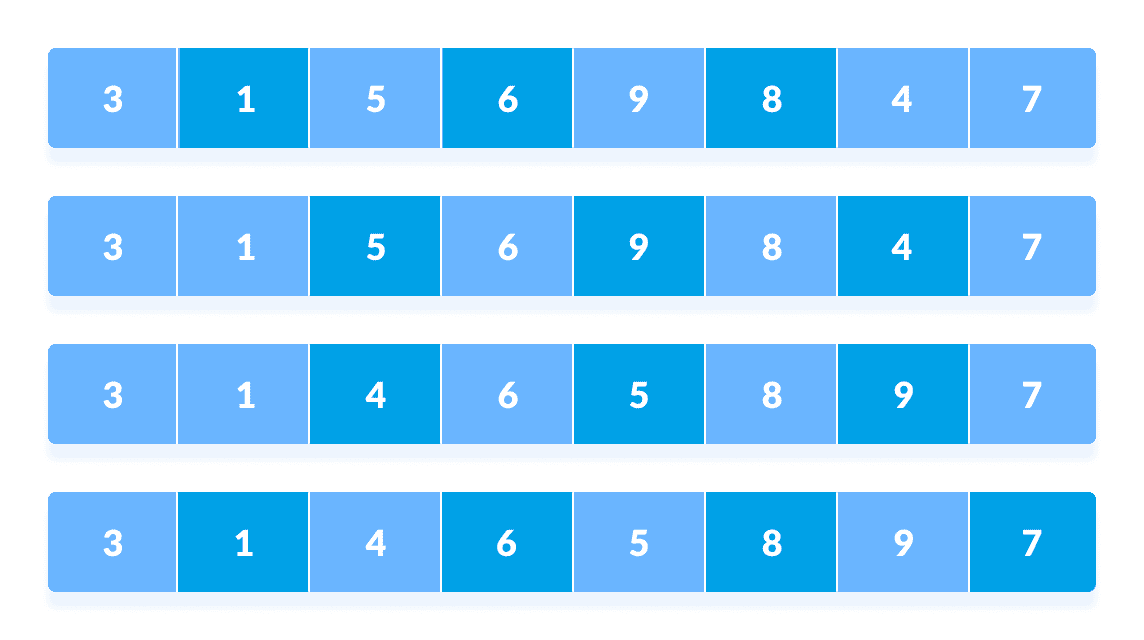
    Shell 排序算法 - 图6
    以n / 4间隔重新排列所有元素

  5. 最后，当间隔为N/8 = 8/8 =1时，将对间隔为 1 的数组元素进行排序。 数组现在已完全排序。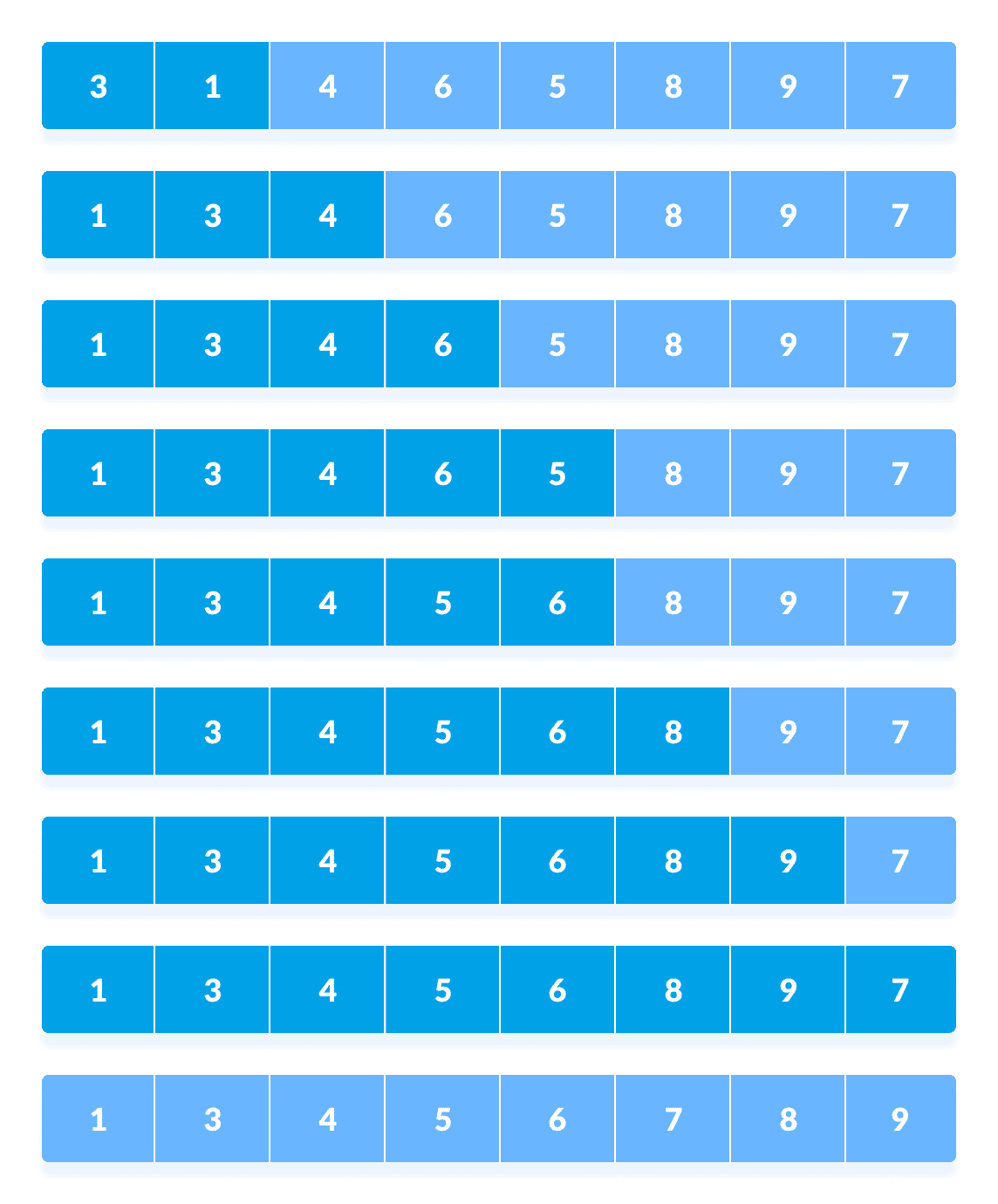
    Shell 排序算法 - 图7
    以n / 8间隔重新排列元素

Shell 排序算法

  1. shellSort(array, size)
  2.   for interval i <- size/2n down to 1
  3.     for each interval "i" in array
  4.         sort all the elements at interval "i"
  5. end shellSort

Python，Java 和 C/C++ 示例

  1. # Shell sort in python
  3. def shellSort(array, n):
  5.     # Rearrange elements at each n/2, n/4, n/8, ... intervals
  6.     interval = n // 2
  7.     while interval > 0:
  8.         for i in range(interval, n):
  9.             temp = array[i]
  10.             j = i
  11.             while j >= interval and array[j - interval] > temp:
  12.                 array[j] = array[j - interval]
  13.                 j -= interval
  15.             array[j] = temp
  16.         interval //= 2
  18. data = [9, 8, 3, 7, 5, 6, 4, 1]
  19. size = len(data)
  20. shellSort(data, size)
  21. print('Sorted Array in Ascending Order:')
  22. print(data)
  1. // Shell sort in Java programming
  3. import java.util.Arrays;
  5. // Shell sort
  6. class ShellSort {
  8.   // Rearrange elements at each n/2, n/4, n/8, ... intervals
  9.   void shellSort(int array[], int n) {
  10.   for (int interval = n / 2; interval > 0; interval /= 2) {
  11.     for (int i = interval; i < n; i += 1) {
  12.     int temp = array[i];
  13.     int j;
  14.     for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
  15.       array[j] = array[j - interval];
  16.     }
  17.     array[j] = temp;
  18.     }
  19.   }
  20.   }
  22.   // Driver code
  23.   public static void main(String args[]) {
  24.   int[] data = { 9, 8, 3, 7, 5, 6, 4, 1 };
  25.   int size = data.length;
  26.   ShellSort ss = new ShellSort();
  27.   ss.shellSort(data, size);
  28.   System.out.println("Sorted Array in Ascending Order: ");
  29.   System.out.println(Arrays.toString(data));
  30.   }
  31. }
  1. // Shell Sort in C programming
  3. #include <stdio.h>
  5. // Shell sort
  6. void shellSort(int array[], int n) {
  7.   // Rearrange elements at each n/2, n/4, n/8, ... intervals
  8.   for (int interval = n / 2; interval > 0; interval /= 2) {
  9.     for (int i = interval; i < n; i += 1) {
  10.       int temp = array[i];
  11.       int j;
  12.       for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
  13.         array[j] = array[j - interval];
  14.       }
  15.       array[j] = temp;
  16.     }
  17.   }
  18. }
  20. // Print an array
  21. void printArray(int array[], int size) {
  22.   for (int i = 0; i < size; ++i) {
  23.     printf("%d  ", array[i]);
  24.   }
  25.   printf("\n");
  26. }
  28. // Driver code
  29. int main() {
  30.   int data[] = {9, 8, 3, 7, 5, 6, 4, 1};
  31.   int size = sizeof(data) / sizeof(data[0]);
  32.   shellSort(data, size);
  33.   printf("Sorted array: \n");
  34.   printArray(data, size);
  35. }
  1. // Shell Sort in C++ programming
  3. #include <iostream>
  4. using namespace std;
  6. // Shell sort
  7. void shellSort(int array[], int n) {
  8.   // Rearrange elements at each n/2, n/4, n/8, ... intervals
  9.   for (int interval = n / 2; interval > 0; interval /= 2) {
  10.     for (int i = interval; i < n; i += 1) {
  11.       int temp = array[i];
  12.       int j;
  13.       for (j = i; j >= interval && array[j - interval] > temp; j -= interval) {
  14.         array[j] = array[j - interval];
  15.       }
  16.       array[j] = temp;
  17.     }
  18.   }
  19. }
  21. // Print an array
  22. void printArray(int array[], int size) {
  23.   int i;
  24.   for (i = 0; i < size; i++)
  25.     cout << array[i] << " ";
  26.   cout << endl;
  27. }
  29. // Driver code
  30. int main() {
  31.   int data[] = {9, 8, 3, 7, 5, 6, 4, 1};
  32.   int size = sizeof(data) / sizeof(data[0]);
  33.   shellSort(data, size);
  34.   cout << "Sorted array: \n";
  35.   printArray(data, size);
  36. }

复杂度

Shell 排序是一种不稳定的排序算法，因为该算法不会检查间隔之间的元素。

时间复杂度

  • 最坏情况复杂度：小于或等于O(n^2)
    外Shell 排序的最坏情况复杂度始终小于或等于O(n^2)。
    根据 Poonen 定理，Shell 排序的最坏情况复杂度是Θ(Nlog N)^2/(log log N)^2)或Θ(Nlog N)^2/log log N)或Θ(N(log N)^2)或介于两者之间。

  • 最佳情况复杂度：O(n*log n)
    对数组进行排序后，每个时间间隔（或增量）的比较总数等于数组的大小。

  • 平均情况复杂度：O(n*log n)
    在O(n^1.25)附近。

复杂程度取决于选择的间隔。 对于选择的不同增量序列，上述复杂度有所不同。 最佳递增顺序未知。

空间复杂度：

外Shell 排序的空间复杂度为O(1)。

Shell 排序应用

在以下情况下使用 Shell 排序：

  • 调用栈是开销。 uClibc 库使用这种排序。
  • 递归超出限制。 bzip2 压缩器使用它。
  • 当接近的元素相距很远时，插入排序的效果不佳。 Shell 排序有助于缩短封闭元素之间的距离。 因此，将执行的交换次数将更少。