图数据结构

原文： https://www.programiz.com/dsa/graph

图数据结构是具有数据并连接到其他节点的节点的集合。

让我们尝试通过一个例子来理解这一点。在 facebook 上，一切都是节点。包括用户，照片，相册，事件，组，页面，评论，故事，视频，链接，注释…任何有数据的都是节点。

每个关系都是从一个节点到另一个节点的一条边。无论您发布照片，加入群组（如页面等），都会为该关系创建新的边。

图数据结构 - 图1

图数据结构示例

然后，所有的 facebook 都是这些节点和边的集合。这是因为 facebook 使用图数据结构来存储其数据。

更准确地说，图是一种数据结构(V, E)，由

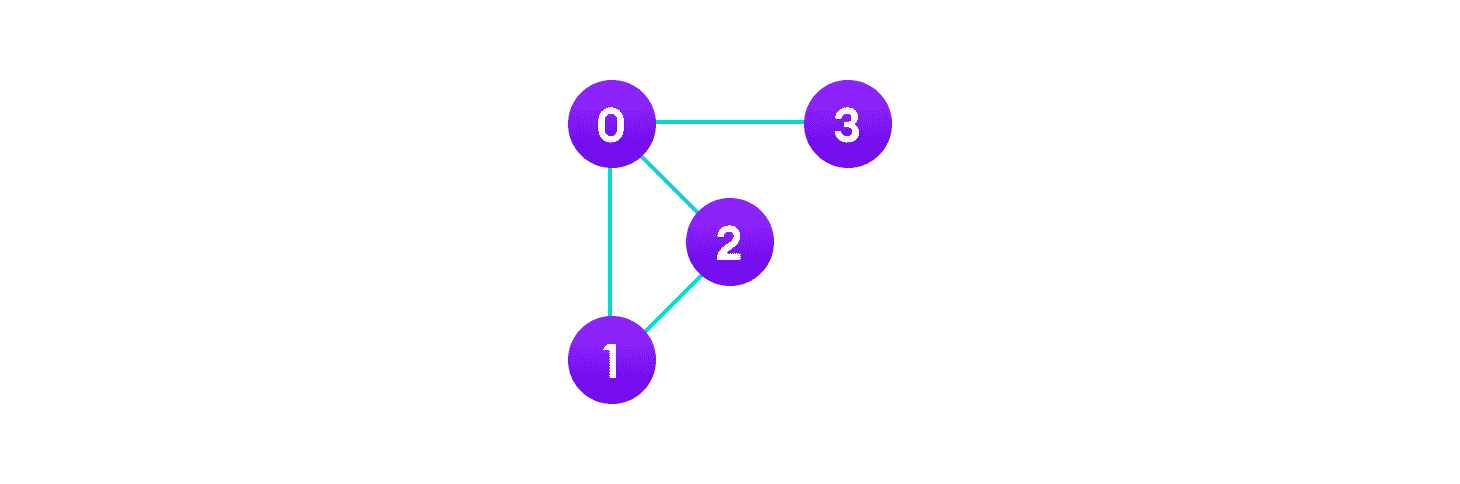
图数据结构 - 图2

顶点和边

在图中，

V = {0, 1, 2, 3}
E = {(0,1), (0,2), (0,3), (1,2)}
G = {V, E}

图的术语

图通常以两种方式表示：

邻接矩阵是V x V顶点的 2D 数组。每行和每列代表一个顶点。

如果任何元素a[i][j]的值为 1，则表示存在连接顶点i和顶点j的边。

我们上面创建的图的邻接矩阵是

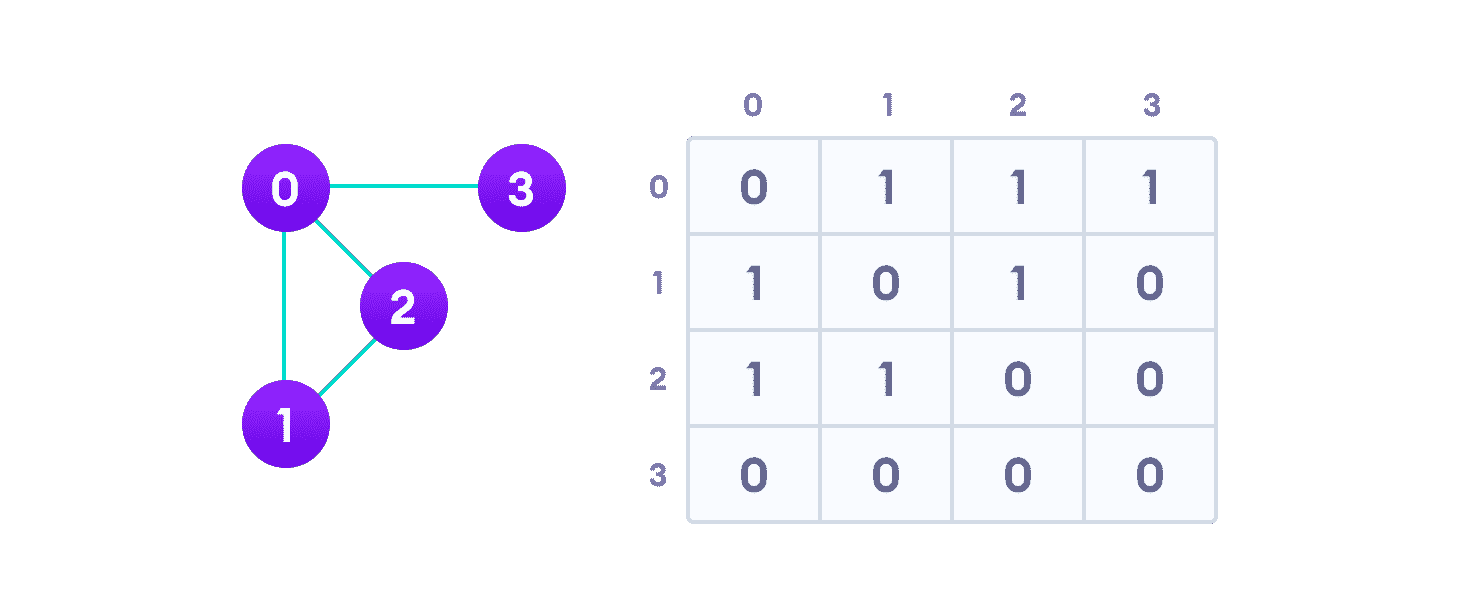
图数据结构 - 图3

图邻接矩阵

由于它是无向图，因此对于边(0, 2)，我们还需要标记边(2, 0)；使邻接矩阵关于对角线对称。

在邻接矩阵表示中，边查找（检查顶点A和顶点B之间是否存在边）非常快，但是我们必须为所有顶点之间的每个可能链接保留空间(V x V)，因此需要更多空间。

邻接列表将图表示为链表的数组。

数组的索引表示一个顶点，而其链表中的每个元素表示与该顶点形成边的其他顶点。

我们在第一个示例中创建的图的邻接列表如下：

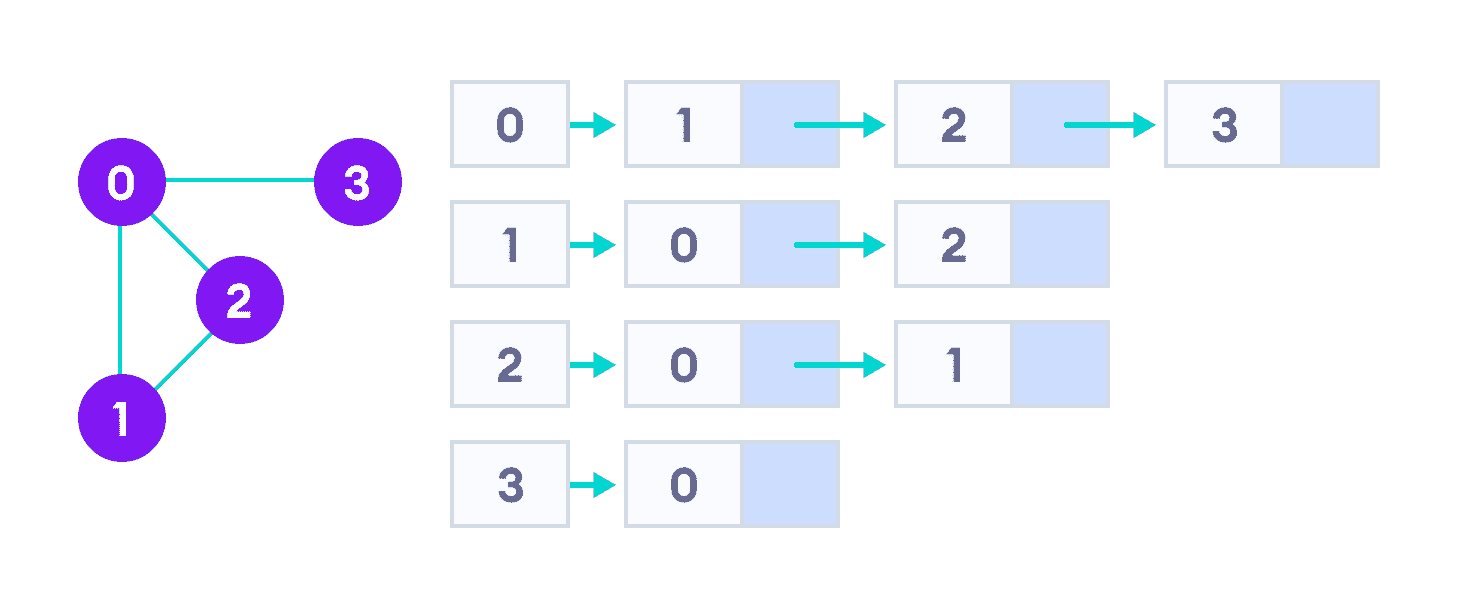
图数据结构 - 图4

邻接表表示

邻接表在存储方面非常有效，因为我们只需要存储边的值即可。对于具有数百万个顶点的图，这可能意味着节省了很多空间。

最常见的图操作是：