原文： https://www.programiz.com/dsa/red-black-tree

在本教程中，您将学习什么是红黑树。 此外，您还将找到在 C，C++ ，Java 和 Python 的红黑树上执行的各种操作的工作示例。

红黑树是一种自平衡二叉搜索树，其中每个节点都包含一个额外的位，用于表示该节点的颜色，红色还是黑色。

一棵红黑树满足以下属性：

  1. 红色/黑色属性：每个节点都是红色或黑色。
  2. 根属性：根是黑色的。
  3. 叶子属性：每片叶子（NIL）是黑色的。
  4. 红色属性：如果红色节点具有子代，则子代始终为黑色。
  5. 深度属性：对于每个节点，从此节点到其任何后代叶子的任何简单路径都具有相同的黑深度（黑节点的数量）。

红黑树的一个示例是：

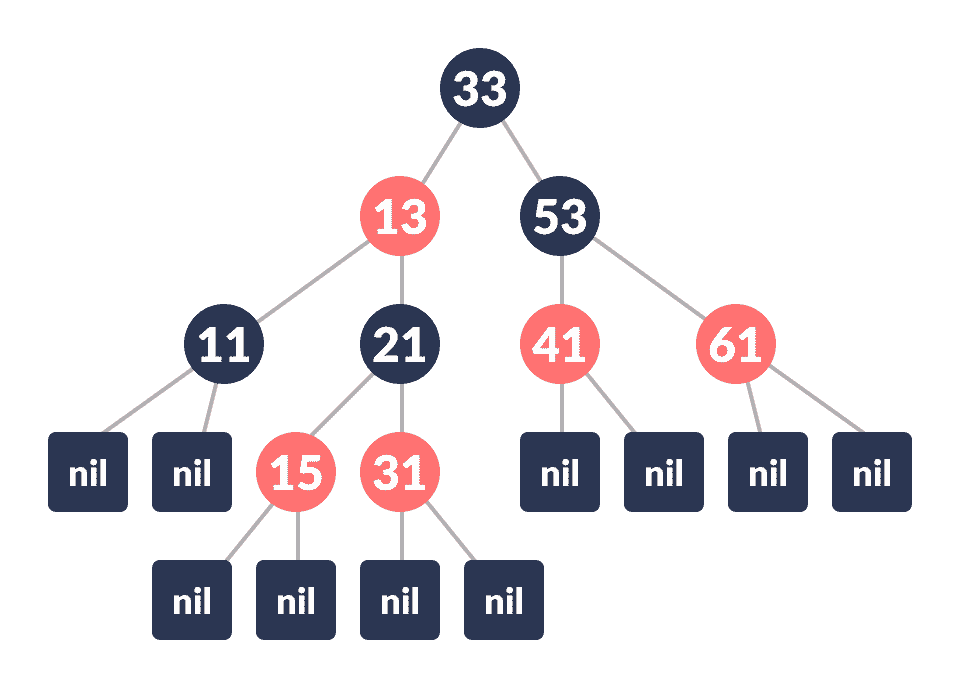
红黑树 - 图1

红黑树

每个节点具有以下属性：

  • 颜色
  • 键
  • 左子级
  • 右子级
  • 父级（根节点除外）

红黑树如何保持自我平衡的性质？

红黑颜色用于平衡树。

节点颜色的限制确保从根到叶的任何简单路径的长度都不会超过其他路径的两倍。 它有助于维持红黑树的自平衡特性。

红黑树上的操作

可以在红黑树上执行的各种操作包括：

旋转红黑树中的子树

在旋转操作中，子树的节点位置互换。

旋转操作用于在其他操作（例如插入和删除）破坏红黑树的属性时维护它们。

轮播有两种类型：

向左旋转

在向左旋转时，右侧节点的排列将转换为左侧节点的排列。

算法

  1. 令初始树为：
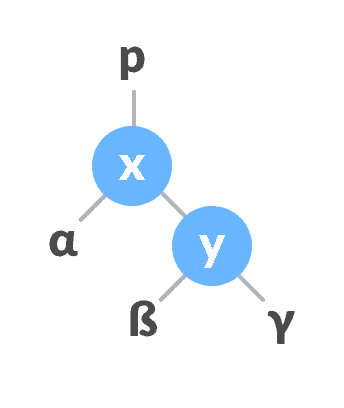
    红黑树 - 图2
    初始树

  2. 如果y具有左子树，则将x分配为y的左子树的父树。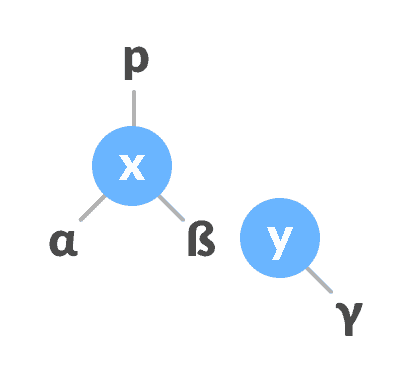
    红黑树 - 图3
    将x分配为y的左子树的父级

  3. 如果x的父级是NULL，则将y作为树的根。

  4. 否则，如果x是p的左子代，则将y设为p的左子代。

  5. 否则，将y分配为p的右子元素。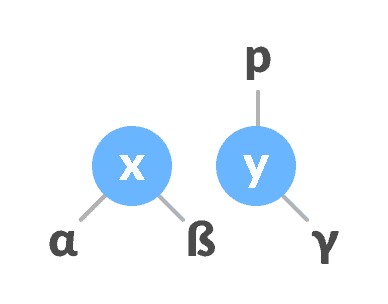
    红黑树 - 图4
    将x的父级更改为y的父级

  6. 将y设为x的父代。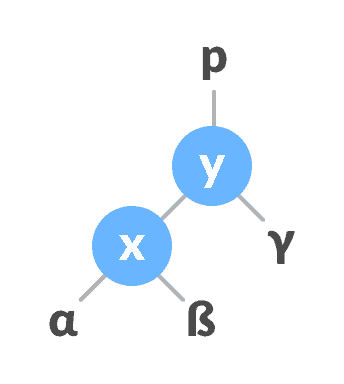
    红黑树 - 图5
    将y指定为x的父代。

向右旋转

在向右旋转时，左侧节点的排列将转换为右侧节点的排列。

  1. 令初始树为：
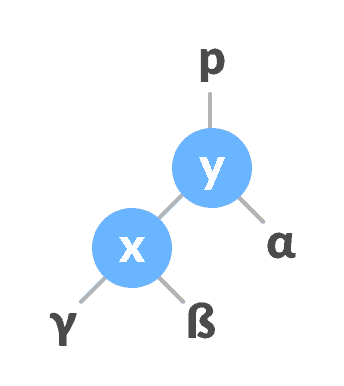
    红黑树 - 图6
    初始树

  2. 如果x具有右子树，则将y分配为x的右子树的父树。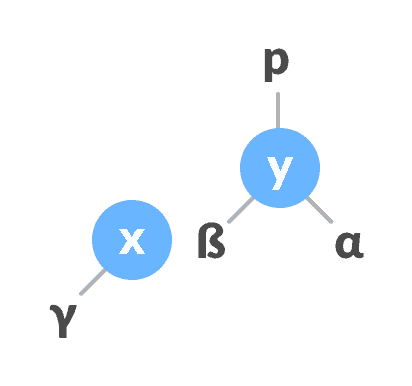
    红黑树 - 图7
    将y分配为x
    的右子树的父级

  3. 如果y的父级为NULL，则将x作为树的根。

  4. 否则，如果y是其父级p的右子，则将x作为p的右子。

  5. 否则，将x分配为p的左子元素。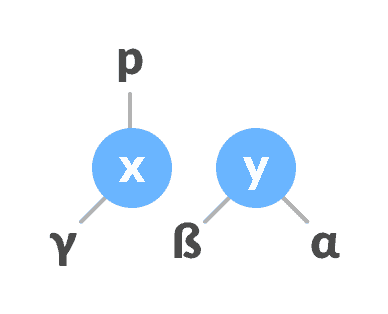
    红黑树 - 图8
    将y的父级指定为x的父级

  6. 使x为y的父代。
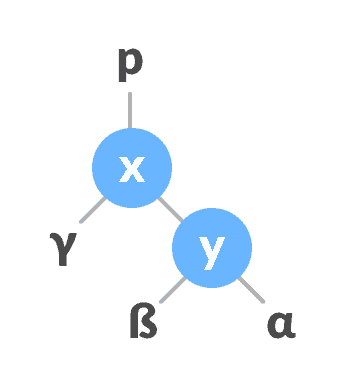
    红黑树 - 图9
    将x分配为y的父项

左右旋转

在左右旋转时，首先将布置向左移动，然后向右移动。

  1. 在x-y上向左旋转。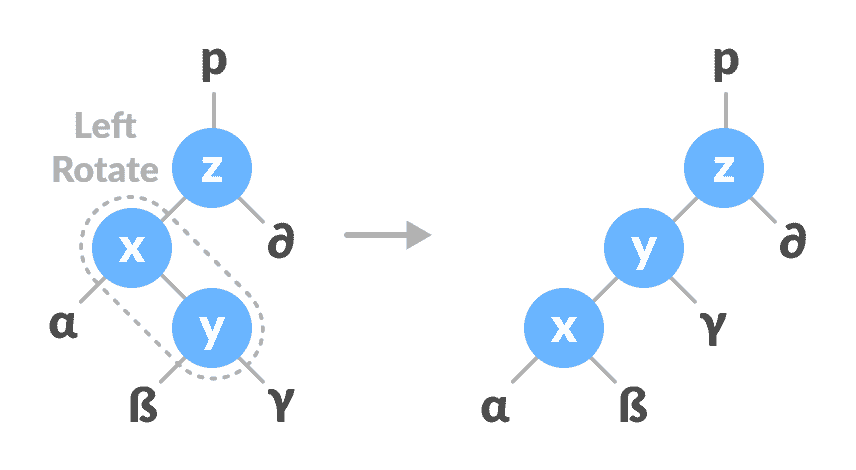
    红黑树 - 图10
    向左旋转x-y

  2. 在y-z上向右旋转。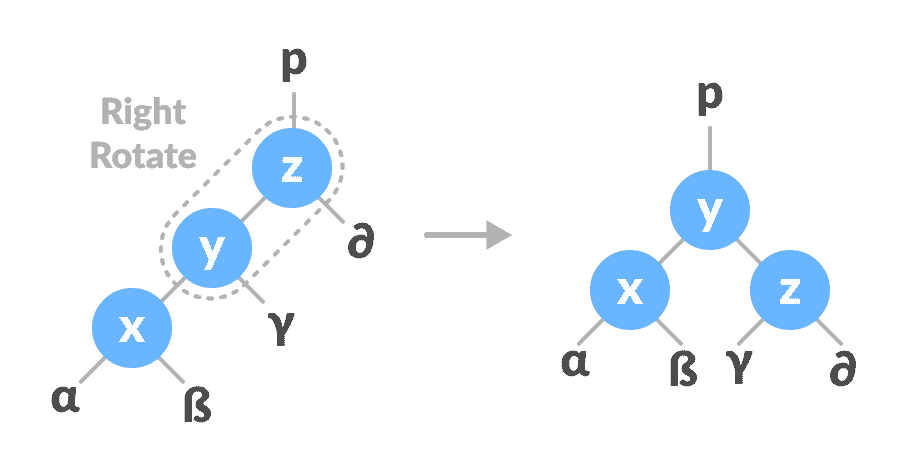
    红黑树 - 图11
    向右旋转z-y

在左右旋转时，排列首先移至右侧，然后移至左侧。

  1. 在x-y上向右旋转。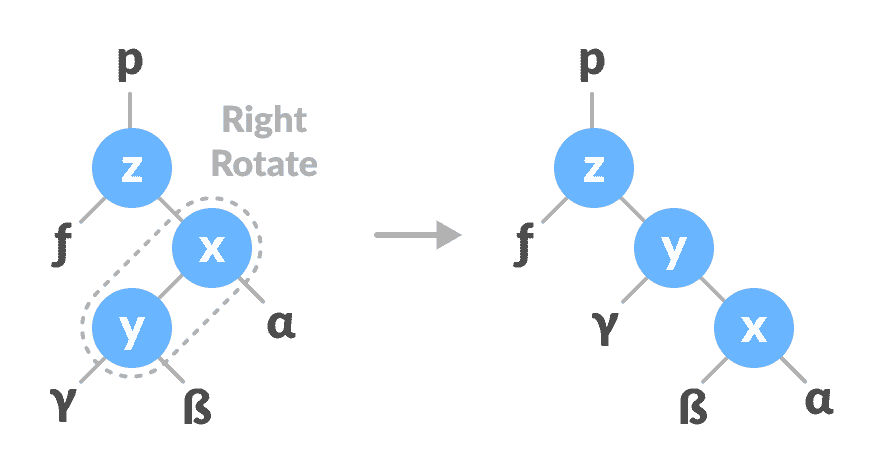
    红黑树 - 图12
    右旋转x-y

  2. 在z-y上向左旋转。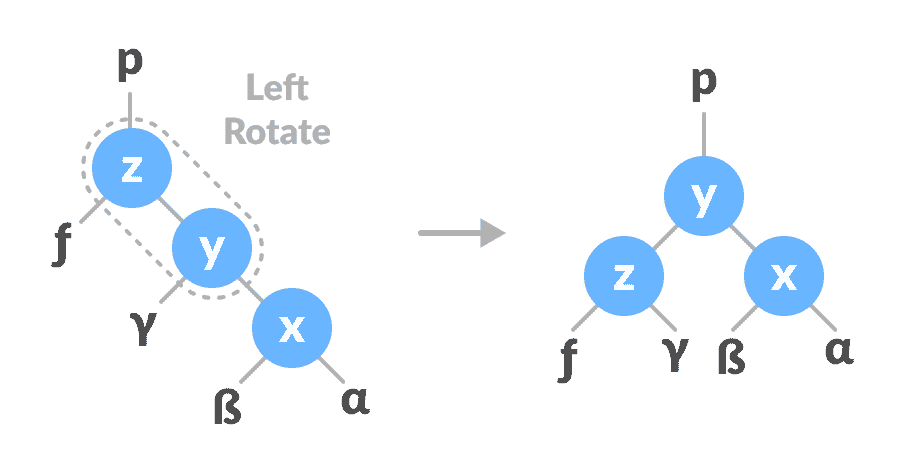
    红黑树 - 图13
    向左旋转z-y

将元素插入红黑树

插入新节点时，新节点始终作为红色节点插入。 插入新节点后，如果树违反了红黑树的属性，则执行以下操作。

  1. 重新着色
  2. 重新旋转

插入节点的算法

按照以下步骤将新元素插入到红黑树中：

  1. 令y为叶子（即NIL），x为树的根。
  2. 检查树是否为空（即x是否为NIL）。 如果是，请插入newNode作为根节点，并将其着色为黑色。

  3. 否则，请重复以下步骤，直到达到叶子（NIL）。

    1. 比较newKey与rootKey。
    2. 如果newKey大于rootKey，则遍历右侧子树。
    3. 否则，遍历左子树。
  4. 将叶子的父级分配为newNode的父级。
  5. 如果leafKey大于newKey，则将newNode设置为rightChild。
  6. 否则，将newNode设置为leftChild。
  7. 在newNode的左侧分配NULL，在右边分配子级。
  8. 为newNode分配红色。
  9. 调用InsertFix算法来维护红黑树的属性（如果违反）。

为什么新插入的节点在红黑树中总是红色？

这是因为插入红色节点不会违反红黑树的depth属性。

如果将红色节点附加到红色节点，则会违反该规则，但是比通过违反depth属性引入的问题更容易解决此问题。

插入后保持红黑属性的算法

如果newNode的插入违反了此属性，则此算法用于维护红黑树的属性。

  1. 进行以下操作，直到newNode p的父级为红色。

  2. 如果p是z的grandParent gP的左子级，请执行以下操作。
    情况一：

    1. 如果z的gP的右子色为红色，则将gP的两个子级分别设置为黑色和红色。
    2. 将gP分配给newNode。
      情况 II：
    3. 否则，如果newNode是p的右子代，则将p分配给newNode。
    4. 向左旋转newNode。
      情况 III：
    5. 将p的颜色设置为黑色，将gP的颜色设置为红色。
    6. 右旋gP。

  3. 否则，请执行以下操作。

    1. 如果z的gP的左子色为红色，则将gP的两个子色分别设为黑色和红色。
    2. 将gP分配给newNode。
    3. 否则，如果newNode是p的左子代，则将p分配给newNode和向右旋转newNode。
    4. 将p的颜色设置为黑色，将gP的颜色设置为红色。
    5. 左旋gP。
  4. 将树的根设置为黑色。

从红黑树中删除元素

此操作从树中删除节点。 删除节点后，再次保留红黑属性。

删除节点的算法

  1. 将nodeToBeDeleted的颜色保存在origrinalColor中。

  2. 如果nodeToBeDeleted的左子级是NULL

    1. 将nodeToBeDeleted的右子代分配给x。
    2. 用x移植nodeToBeDeleted。

  3. 否则，如果nodeToBeDeleted的右子对象是NULL

    1. 将nodeToBeDeleted的左子级分配到x中。
    2. 用x移植nodeToBeDeleted。

  4. 其他

    1. 将noteToBeDeleted的右子树的最小值分配到y中。
    2. 将sum的颜色保存在originalColor中。
    3. 将y的rightChild分配到x中。
    4. 如果y是nodeToBeDeleted的子级，则将x的父级设置为y。
    5. 否则，将y移植为y的rightChild。
    6. 将sum移植到nodeToBeDeleted中。
    7. 使用originalColor设置y的颜色。
  5. 如果originalColor为黑色，则调用DeleteFix(x)。

删除后保持红黑属性的算法

当删除黑色节点时会执行此算法，因为它违反了红黑树的黑色深度属性。

通过假定节点x（占据y的原始位置）具有额外的黑色来纠正此冲突。 这使得节点x既不是红色的，也不是黑色的。 它是双黑色或黑色和红色。 这违反了红黑色属性。

但是，x的颜色属性未更改，而是在指向节点的x的表示中表示了额外的黑色。

如果多余的黑色可以去除

  1. 它到达根节点。
  2. 如果x指向红黑节点。 在这种情况下，x被涂成黑色。
  3. 进行适当的旋转和重新着色。

以下算法保留了红黑树的属性。

  1. 执行以下操作，直到x不是树的根并且x的颜色为黑色

  2. 如果x是其父级的左子级，

    1. 将w分配给x的同级。

    2. 如果x的父级的右子是红色，则
      情况 I：

      1. 将x的父级的右子级的颜色设置为黑色。
      2. 将x的父级颜色设置为红色。
      3. 左旋转x的父级。
      4. 将x的父级的rightChild分配给w。

    3. 如果w的右侧和leftChild的颜色均为黑色，则
      情况 II：

      1. 将w的颜色设置为红色
      2. 将x的父级分配给x。

    4. 否则，如果w的rightChild的颜色是黑色
      情况 III：

      1. 将w的leftChild的颜色设置为黑色
      2. 将w的颜色设置为红色
      3. 向右旋转w。
      4. 将x的父级的rightChild分配给w。

    5. 如果以上情况均未发生，请执行以下操作。
      情况 IV：

      1. 将w的颜色设置为x的父代的颜色。
      2. 将x的父级的颜色设置为黑色。
      3. 将w的右子元素的颜色设置为黑色。
      4. 左旋转x的父级。
      5. 将x设置为树的根。
  3. 其他与上述相同，将右侧更改为左侧，反之亦然。
  4. 将x的颜色设置为黑色。

有关示例的更多说明，请参见插入和删除操作。

Python，Java 和 C/C++ 示例

  1. # Implementing Red-Black Tree in Python
  3. import sys
  5. # Node creation
  6. class Node():
  7.     def __init__(self, item):
  8.         self.item = item
  9.         self.parent = None
  10.         self.left = None
  11.         self.right = None
  12.         self.color = 1
  14. class RedBlackTree():
  15.     def __init__(self):
  16.         self.TNULL = Node(0)
  17.         self.TNULL.color = 0
  18.         self.TNULL.left = None
  19.         self.TNULL.right = None
  20.         self.root = self.TNULL
  22.     # Preorder
  23.     def pre_order_helper(self, node):
  24.         if node != TNULL:
  25.             sys.stdout.write(node.item + " ")
  26.             self.pre_order_helper(node.left)
  27.             self.pre_order_helper(node.right)
  29.     # Inorder
  30.     def in_order_helper(self, node):
  31.         if node != TNULL:
  32.             self.in_order_helper(node.left)
  33.             sys.stdout.write(node.item + " ")
  34.             self.in_order_helper(node.right)
  36.     # Postorder
  37.     def post_order_helper(self, node):
  38.         if node != TNULL:
  39.             self.post_order_helper(node.left)
  40.             self.post_order_helper(node.right)
  41.             sys.stdout.write(node.item + " ")
  43.     # Search the tree
  44.     def search_tree_helper(self, node, key):
  45.         if node == TNULL or key == node.item:
  46.             return node
  48.         if key < node.item:
  49.             return self.search_tree_helper(node.left, key)
  50.         return self.search_tree_helper(node.right, key)
  52.     # Balancing the tree after deletion
  53.     def delete_fix(self, x):
  54.         while x != self.root and x.color == 0:
  55.             if x == x.parent.left:
  56.                 s = x.parent.right
  57.                 if s.color == 1:
  58.                     s.color = 0
  59.                     x.parent.color = 1
  60.                     self.left_rotate(x.parent)
  61.                     s = x.parent.right
  63.                 if s.left.color == 0 and s.right.color == 0:
  64.                     s.color = 1
  65.                     x = x.parent
  66.                 else:
  67.                     if s.right.color == 0:
  68.                         s.left.color = 0
  69.                         s.color = 1
  70.                         self.right_rotate(s)
  71.                         s = x.parent.right
  73.                     s.color = x.parent.color
  74.                     x.parent.color = 0
  75.                     s.right.color = 0
  76.                     self.left_rotate(x.parent)
  77.                     x = self.root
  78.             else:
  79.                 s = x.parent.left
  80.                 if s.color == 1:
  81.                     s.color = 0
  82.                     x.parent.color = 1
  83.                     self.right_rotate(x.parent)
  84.                     s = x.parent.left
  86.                 if s.right.color == 0 and s.right.color == 0:
  87.                     s.color = 1
  88.                     x = x.parent
  89.                 else:
  90.                     if s.left.color == 0:
  91.                         s.right.color = 0
  92.                         s.color = 1
  93.                         self.left_rotate(s)
  94.                         s = x.parent.left
  96.                     s.color = x.parent.color
  97.                     x.parent.color = 0
  98.                     s.left.color = 0
  99.                     self.right_rotate(x.parent)
  100.                     x = self.root
  101.         x.color = 0
  103.     def __rb_transplant(self, u, v):
  104.         if u.parent == None:
  105.             self.root = v
  106.         elif u == u.parent.left:
  107.             u.parent.left = v
  108.         else:
  109.             u.parent.right = v
  110.         v.parent = u.parent
  112.     # Node deletion
  113.     def delete_node_helper(self, node, key):
  114.         z = self.TNULL
  115.         while node != self.TNULL:
  116.             if node.item == key:
  117.                 z = node
  119.             if node.item <= key:
  120.                 node = node.right
  121.             else:
  122.                 node = node.left
  124.         if z == self.TNULL:
  125.             print("Cannot find key in the tree")
  126.             return
  128.         y = z
  129.         y_original_color = y.color
  130.         if z.left == self.TNULL:
  131.             x = z.right
  132.             self.__rb_transplant(z, z.right)
  133.         elif (z.right == self.TNULL):
  134.             x = z.left
  135.             self.__rb_transplant(z, z.left)
  136.         else:
  137.             y = self.minimum(z.right)
  138.             y_original_color = y.color
  139.             x = y.right
  140.             if y.parent == z:
  141.                 x.parent = y
  142.             else:
  143.                 self.__rb_transplant(y, y.right)
  144.                 y.right = z.right
  145.                 y.right.parent = y
  147.             self.__rb_transplant(z, y)
  148.             y.left = z.left
  149.             y.left.parent = y
  150.             y.color = z.color
  151.         if y_original_color == 0:
  152.             self.delete_fix(x)
  154.     # Balance the tree after insertion
  155.     def fix_insert(self, k):
  156.         while k.parent.color == 1:
  157.             if k.parent == k.parent.parent.right:
  158.                 u = k.parent.parent.left
  159.                 if u.color == 1:
  160.                     u.color = 0
  161.                     k.parent.color = 0
  162.                     k.parent.parent.color = 1
  163.                     k = k.parent.parent
  164.                 else:
  165.                     if k == k.parent.left:
  166.                         k = k.parent
  167.                         self.right_rotate(k)
  168.                     k.parent.color = 0
  169.                     k.parent.parent.color = 1
  170.                     self.left_rotate(k.parent.parent)
  171.             else:
  172.                 u = k.parent.parent.right
  174.                 if u.color == 1:
  175.                     u.color = 0
  176.                     k.parent.color = 0
  177.                     k.parent.parent.color = 1
  178.                     k = k.parent.parent
  179.                 else:
  180.                     if k == k.parent.right:
  181.                         k = k.parent
  182.                         self.left_rotate(k)
  183.                     k.parent.color = 0
  184.                     k.parent.parent.color = 1
  185.                     self.right_rotate(k.parent.parent)
  186.             if k == self.root:
  187.                 break
  188.         self.root.color = 0
  190.     # Printing the tree
  191.     def __print_helper(self, node, indent, last):
  192.         if node != self.TNULL:
  193.             sys.stdout.write(indent)
  194.             if last:
  195.                 sys.stdout.write("R----")
  196.                 indent += "     "
  197.             else:
  198.                 sys.stdout.write("L----")
  199.                 indent += "|    "
  201.             s_color = "RED" if node.color == 1 else "BLACK"
  202.             print(str(node.item) + "(" + s_color + ")")
  203.             self.__print_helper(node.left, indent, False)
  204.             self.__print_helper(node.right, indent, True)
  206.     def preorder(self):
  207.         self.pre_order_helper(self.root)
  209.     def inorder(self):
  210.         self.in_order_helper(self.root)
  212.     def postorder(self):
  213.         self.post_order_helper(self.root)
  215.     def searchTree(self, k):
  216.         return self.search_tree_helper(self.root, k)
  218.     def minimum(self, node):
  219.         while node.left != self.TNULL:
  220.             node = node.left
  221.         return node
  223.     def maximum(self, node):
  224.         while node.right != self.TNULL:
  225.             node = node.right
  226.         return node
  228.     def successor(self, x):
  229.         if x.right != self.TNULL:
  230.             return self.minimum(x.right)
  232.         y = x.parent
  233.         while y != self.TNULL and x == y.right:
  234.             x = y
  235.             y = y.parent
  236.         return y
  238.     def predecessor(self,  x):
  239.         if (x.left != self.TNULL):
  240.             return self.maximum(x.left)
  242.         y = x.parent
  243.         while y != self.TNULL and x == y.left:
  244.             x = y
  245.             y = y.parent
  247.         return y
  249.     def left_rotate(self, x):
  250.         y = x.right
  251.         x.right = y.left
  252.         if y.left != self.TNULL:
  253.             y.left.parent = x
  255.         y.parent = x.parent
  256.         if x.parent == None:
  257.             self.root = y
  258.         elif x == x.parent.left:
  259.             x.parent.left = y
  260.         else:
  261.             x.parent.right = y
  262.         y.left = x
  263.         x.parent = y
  265.     def right_rotate(self, x):
  266.         y = x.left
  267.         x.left = y.right
  268.         if y.right != self.TNULL:
  269.             y.right.parent = x
  271.         y.parent = x.parent
  272.         if x.parent == None:
  273.             self.root = y
  274.         elif x == x.parent.right:
  275.             x.parent.right = y
  276.         else:
  277.             x.parent.left = y
  278.         y.right = x
  279.         x.parent = y
  281.     def insert(self, key):
  282.         node = Node(key)
  283.         node.parent = None
  284.         node.item = key
  285.         node.left = self.TNULL
  286.         node.right = self.TNULL
  287.         node.color = 1
  289.         y = None
  290.         x = self.root
  292.         while x != self.TNULL:
  293.             y = x
  294.             if node.item < x.item:
  295.                 x = x.left
  296.             else:
  297.                 x = x.right
  299.         node.parent = y
  300.         if y == None:
  301.             self.root = node
  302.         elif node.item < y.item:
  303.             y.left = node
  304.         else:
  305.             y.right = node
  307.         if node.parent == None:
  308.             node.color = 0
  309.             return
  311.         if node.parent.parent == None:
  312.             return
  314.         self.fix_insert(node)
  316.     def get_root(self):
  317.         return self.root
  319.     def delete_node(self, item):
  320.         self.delete_node_helper(self.root, item)
  322.     def print_tree(self):
  323.         self.__print_helper(self.root, "", True)
  325. if __name__ == "__main__":
  326.     bst = RedBlackTree()
  328.     bst.insert(55)
  329.     bst.insert(40)
  330.     bst.insert(65)
  331.     bst.insert(60)
  332.     bst.insert(75)
  333.     bst.insert(57)
  335.     bst.print_tree()
  337.     print("\nAfter deleting an element")
  338.     bst.delete_node(40)
  339.     bst.print_tree()
// Implementing Red-Black Tree in Java

class Node {
  int data;
  Node parent;
  Node left;
  Node right;
  int color;
}

public class RedBlackTree {
  private Node root;
  private Node TNULL;

  // Preorder
  private void preOrderHelper(Node node) {
    if (node != TNULL) {
      System.out.print(node.data + " ");
      preOrderHelper(node.left);
      preOrderHelper(node.right);
    }
  }

  // Inorder
  private void inOrderHelper(Node node) {
    if (node != TNULL) {
      inOrderHelper(node.left);
      System.out.print(node.data + " ");
      inOrderHelper(node.right);
    }
  }

  // Post order
  private void postOrderHelper(Node node) {
    if (node != TNULL) {
      postOrderHelper(node.left);
      postOrderHelper(node.right);
      System.out.print(node.data + " ");
    }
  }

  // Search the tree
  private Node searchTreeHelper(Node node, int key) {
    if (node == TNULL || key == node.data) {
      return node;
    }

    if (key < node.data) {
      return searchTreeHelper(node.left, key);
    }
    return searchTreeHelper(node.right, key);
  }

  // Balance the tree after deletion of a node
  private void fixDelete(Node x) {
    Node s;
    while (x != root && x.color == 0) {
      if (x == x.parent.left) {
        s = x.parent.right;
        if (s.color == 1) {
          s.color = 0;
          x.parent.color = 1;
          leftRotate(x.parent);
          s = x.parent.right;
        }

        if (s.left.color == 0 && s.right.color == 0) {
          s.color = 1;
          x = x.parent;
        } else {
          if (s.right.color == 0) {
            s.left.color = 0;
            s.color = 1;
            rightRotate(s);
            s = x.parent.right;
          }

          s.color = x.parent.color;
          x.parent.color = 0;
          s.right.color = 0;
          leftRotate(x.parent);
          x = root;
        }
      } else {
        s = x.parent.left;
        if (s.color == 1) {
          s.color = 0;
          x.parent.color = 1;
          rightRotate(x.parent);
          s = x.parent.left;
        }

        if (s.right.color == 0 && s.right.color == 0) {
          s.color = 1;
          x = x.parent;
        } else {
          if (s.left.color == 0) {
            s.right.color = 0;
            s.color = 1;
            leftRotate(s);
            s = x.parent.left;
          }

          s.color = x.parent.color;
          x.parent.color = 0;
          s.left.color = 0;
          rightRotate(x.parent);
          x = root;
        }
      }
    }
    x.color = 0;
  }

  private void rbTransplant(Node u, Node v) {
    if (u.parent == null) {
      root = v;
    } else if (u == u.parent.left) {
      u.parent.left = v;
    } else {
      u.parent.right = v;
    }
    v.parent = u.parent;
  }

  private void deleteNodeHelper(Node node, int key) {
    Node z = TNULL;
    Node x, y;
    while (node != TNULL) {
      if (node.data == key) {
        z = node;
      }

      if (node.data <= key) {
        node = node.right;
      } else {
        node = node.left;
      }
    }

    if (z == TNULL) {
      System.out.println("Couldn't find key in the tree");
      return;
    }

    y = z;
    int yOriginalColor = y.color;
    if (z.left == TNULL) {
      x = z.right;
      rbTransplant(z, z.right);
    } else if (z.right == TNULL) {
      x = z.left;
      rbTransplant(z, z.left);
    } else {
      y = minimum(z.right);
      yOriginalColor = y.color;
      x = y.right;
      if (y.parent == z) {
        x.parent = y;
      } else {
        rbTransplant(y, y.right);
        y.right = z.right;
        y.right.parent = y;
      }

      rbTransplant(z, y);
      y.left = z.left;
      y.left.parent = y;
      y.color = z.color;
    }
    if (yOriginalColor == 0) {
      fixDelete(x);
    }
  }

  // Balance the node after insertion
  private void fixInsert(Node k) {
    Node u;
    while (k.parent.color == 1) {
      if (k.parent == k.parent.parent.right) {
        u = k.parent.parent.left;
        if (u.color == 1) {
          u.color = 0;
          k.parent.color = 0;
          k.parent.parent.color = 1;
          k = k.parent.parent;
        } else {
          if (k == k.parent.left) {
            k = k.parent;
            rightRotate(k);
          }
          k.parent.color = 0;
          k.parent.parent.color = 1;
          leftRotate(k.parent.parent);
        }
      } else {
        u = k.parent.parent.right;

        if (u.color == 1) {
          u.color = 0;
          k.parent.color = 0;
          k.parent.parent.color = 1;
          k = k.parent.parent;
        } else {
          if (k == k.parent.right) {
            k = k.parent;
            leftRotate(k);
          }
          k.parent.color = 0;
          k.parent.parent.color = 1;
          rightRotate(k.parent.parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root.color = 0;
  }

  private void printHelper(Node root, String indent, boolean last) {
    if (root != TNULL) {
      System.out.print(indent);
      if (last) {
        System.out.print("R----");
        indent += "   ";
      } else {
        System.out.print("L----");
        indent += "|  ";
      }

      String sColor = root.color == 1 ? "RED" : "BLACK";
      System.out.println(root.data + "(" + sColor + ")");
      printHelper(root.left, indent, false);
      printHelper(root.right, indent, true);
    }
  }

  public RedBlackTree() {
    TNULL = new Node();
    TNULL.color = 0;
    TNULL.left = null;
    TNULL.right = null;
    root = TNULL;
  }

  public void preorder() {
    preOrderHelper(this.root);
  }

  public void inorder() {
    inOrderHelper(this.root);
  }

  public void postorder() {
    postOrderHelper(this.root);
  }

  public Node searchTree(int k) {
    return searchTreeHelper(this.root, k);
  }

  public Node minimum(Node node) {
    while (node.left != TNULL) {
      node = node.left;
    }
    return node;
  }

  public Node maximum(Node node) {
    while (node.right != TNULL) {
      node = node.right;
    }
    return node;
  }

  public Node successor(Node x) {
    if (x.right != TNULL) {
      return minimum(x.right);
    }

    Node y = x.parent;
    while (y != TNULL && x == y.right) {
      x = y;
      y = y.parent;
    }
    return y;
  }

  public Node predecessor(Node x) {
    if (x.left != TNULL) {
      return maximum(x.left);
    }

    Node y = x.parent;
    while (y != TNULL && x == y.left) {
      x = y;
      y = y.parent;
    }

    return y;
  }

  public void leftRotate(Node x) {
    Node y = x.right;
    x.right = y.left;
    if (y.left != TNULL) {
      y.left.parent = x;
    }
    y.parent = x.parent;
    if (x.parent == null) {
      this.root = y;
    } else if (x == x.parent.left) {
      x.parent.left = y;
    } else {
      x.parent.right = y;
    }
    y.left = x;
    x.parent = y;
  }

  public void rightRotate(Node x) {
    Node y = x.left;
    x.left = y.right;
    if (y.right != TNULL) {
      y.right.parent = x;
    }
    y.parent = x.parent;
    if (x.parent == null) {
      this.root = y;
    } else if (x == x.parent.right) {
      x.parent.right = y;
    } else {
      x.parent.left = y;
    }
    y.right = x;
    x.parent = y;
  }

  public void insert(int key) {
    Node node = new Node();
    node.parent = null;
    node.data = key;
    node.left = TNULL;
    node.right = TNULL;
    node.color = 1;

    Node y = null;
    Node x = this.root;

    while (x != TNULL) {
      y = x;
      if (node.data < x.data) {
        x = x.left;
      } else {
        x = x.right;
      }
    }

    node.parent = y;
    if (y == null) {
      root = node;
    } else if (node.data < y.data) {
      y.left = node;
    } else {
      y.right = node;
    }

    if (node.parent == null) {
      node.color = 0;
      return;
    }

    if (node.parent.parent == null) {
      return;
    }

    fixInsert(node);
  }

  public Node getRoot() {
    return this.root;
  }

  public void deleteNode(int data) {
    deleteNodeHelper(this.root, data);
  }

  public void printTree() {
    printHelper(this.root, "", true);
  }

  public static void main(String[] args) {
    RedBlackTree bst = new RedBlackTree();
    bst.insert(55);
    bst.insert(40);
    bst.insert(65);
    bst.insert(60);
    bst.insert(75);
    bst.insert(57);
    bst.printTree();

    System.out.println("\nAfter deleting:");
    bst.deleteNode(40);
    bst.printTree();
  }
}

// Implementing Red-Black Tree in C

#include <stdio.h>
#include <stdlib.h>

enum nodeColor {
  RED,
  BLACK
};

struct rbNode {
  int data, color;
  struct rbNode *link[2];
};

struct rbNode *root = NULL;

// Create a red-black tree
struct rbNode *createNode(int data) {
  struct rbNode *newnode;
  newnode = (struct rbNode *)malloc(sizeof(struct rbNode));
  newnode->data = data;
  newnode->color = RED;
  newnode->link[0] = newnode->link[1] = NULL;
  return newnode;
}

// Insert an node
void insertion(int data) {
  struct rbNode *stack[98], *ptr, *newnode, *xPtr, *yPtr;
  int dir[98], ht = 0, index;
  ptr = root;
  if (!root) {
    root = createNode(data);
    return;
  }

  stack[ht] = root;
  dir[ht++] = 0;
  while (ptr != NULL) {
    if (ptr->data == data) {
      printf("Duplicates Not Allowed!!\n");
      return;
    }
    index = (data - ptr->data) > 0 ? 1 : 0;
    stack[ht] = ptr;
    ptr = ptr->link[index];
    dir[ht++] = index;
  }
  stack[ht - 1]->link[index] = newnode = createNode(data);
  while ((ht >= 3) && (stack[ht - 1]->color == RED)) {
    if (dir[ht - 2] == 0) {
      yPtr = stack[ht - 2]->link[1];
      if (yPtr != NULL && yPtr->color == RED) {
        stack[ht - 2]->color = RED;
        stack[ht - 1]->color = yPtr->color = BLACK;
        ht = ht - 2;
      } else {
        if (dir[ht - 1] == 0) {
          yPtr = stack[ht - 1];
        } else {
          xPtr = stack[ht - 1];
          yPtr = xPtr->link[1];
          xPtr->link[1] = yPtr->link[0];
          yPtr->link[0] = xPtr;
          stack[ht - 2]->link[0] = yPtr;
        }
        xPtr = stack[ht - 2];
        xPtr->color = RED;
        yPtr->color = BLACK;
        xPtr->link[0] = yPtr->link[1];
        yPtr->link[1] = xPtr;
        if (xPtr == root) {
          root = yPtr;
        } else {
          stack[ht - 3]->link[dir[ht - 3]] = yPtr;
        }
        break;
      }
    } else {
      yPtr = stack[ht - 2]->link[0];
      if ((yPtr != NULL) && (yPtr->color == RED)) {
        stack[ht - 2]->color = RED;
        stack[ht - 1]->color = yPtr->color = BLACK;
        ht = ht - 2;
      } else {
        if (dir[ht - 1] == 1) {
          yPtr = stack[ht - 1];
        } else {
          xPtr = stack[ht - 1];
          yPtr = xPtr->link[0];
          xPtr->link[0] = yPtr->link[1];
          yPtr->link[1] = xPtr;
          stack[ht - 2]->link[1] = yPtr;
        }
        xPtr = stack[ht - 2];
        yPtr->color = BLACK;
        xPtr->color = RED;
        xPtr->link[1] = yPtr->link[0];
        yPtr->link[0] = xPtr;
        if (xPtr == root) {
          root = yPtr;
        } else {
          stack[ht - 3]->link[dir[ht - 3]] = yPtr;
        }
        break;
      }
    }
  }
  root->color = BLACK;
}

// Delete a node
void deletion(int data) {
  struct rbNode *stack[98], *ptr, *xPtr, *yPtr;
  struct rbNode *pPtr, *qPtr, *rPtr;
  int dir[98], ht = 0, diff, i;
  enum nodeColor color;

  if (!root) {
    printf("Tree not available\n");
    return;
  }

  ptr = root;
  while (ptr != NULL) {
    if ((data - ptr->data) == 0)
      break;
    diff = (data - ptr->data) > 0 ? 1 : 0;
    stack[ht] = ptr;
    dir[ht++] = diff;
    ptr = ptr->link[diff];
  }

  if (ptr->link[1] == NULL) {
    if ((ptr == root) && (ptr->link[0] == NULL)) {
      free(ptr);
      root = NULL;
    } else if (ptr == root) {
      root = ptr->link[0];
      free(ptr);
    } else {
      stack[ht - 1]->link[dir[ht - 1]] = ptr->link[0];
    }
  } else {
    xPtr = ptr->link[1];
    if (xPtr->link[0] == NULL) {
      xPtr->link[0] = ptr->link[0];
      color = xPtr->color;
      xPtr->color = ptr->color;
      ptr->color = color;

      if (ptr == root) {
        root = xPtr;
      } else {
        stack[ht - 1]->link[dir[ht - 1]] = xPtr;
      }

      dir[ht] = 1;
      stack[ht++] = xPtr;
    } else {
      i = ht++;
      while (1) {
        dir[ht] = 0;
        stack[ht++] = xPtr;
        yPtr = xPtr->link[0];
        if (!yPtr->link[0])
          break;
        xPtr = yPtr;
      }

      dir[i] = 1;
      stack[i] = yPtr;
      if (i > 0)
        stack[i - 1]->link[dir[i - 1]] = yPtr;

      yPtr->link[0] = ptr->link[0];

      xPtr->link[0] = yPtr->link[1];
      yPtr->link[1] = ptr->link[1];

      if (ptr == root) {
        root = yPtr;
      }

      color = yPtr->color;
      yPtr->color = ptr->color;
      ptr->color = color;
    }
  }

  if (ht < 1)
    return;

  if (ptr->color == BLACK) {
    while (1) {
      pPtr = stack[ht - 1]->link[dir[ht - 1]];
      if (pPtr && pPtr->color == RED) {
        pPtr->color = BLACK;
        break;
      }

      if (ht < 2)
        break;

      if (dir[ht - 2] == 0) {
        rPtr = stack[ht - 1]->link[1];

        if (!rPtr)
          break;

        if (rPtr->color == RED) {
          stack[ht - 1]->color = RED;
          rPtr->color = BLACK;
          stack[ht - 1]->link[1] = rPtr->link[0];
          rPtr->link[0] = stack[ht - 1];

          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          dir[ht] = 0;
          stack[ht] = stack[ht - 1];
          stack[ht - 1] = rPtr;
          ht++;

          rPtr = stack[ht - 1]->link[1];
        }

        if ((!rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
          (!rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
          rPtr->color = RED;
        } else {
          if (!rPtr->link[1] || rPtr->link[1]->color == BLACK) {
            qPtr = rPtr->link[0];
            rPtr->color = RED;
            qPtr->color = BLACK;
            rPtr->link[0] = qPtr->link[1];
            qPtr->link[1] = rPtr;
            rPtr = stack[ht - 1]->link[1] = qPtr;
          }
          rPtr->color = stack[ht - 1]->color;
          stack[ht - 1]->color = BLACK;
          rPtr->link[1]->color = BLACK;
          stack[ht - 1]->link[1] = rPtr->link[0];
          rPtr->link[0] = stack[ht - 1];
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          break;
        }
      } else {
        rPtr = stack[ht - 1]->link[0];
        if (!rPtr)
          break;

        if (rPtr->color == RED) {
          stack[ht - 1]->color = RED;
          rPtr->color = BLACK;
          stack[ht - 1]->link[0] = rPtr->link[1];
          rPtr->link[1] = stack[ht - 1];

          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          dir[ht] = 1;
          stack[ht] = stack[ht - 1];
          stack[ht - 1] = rPtr;
          ht++;

          rPtr = stack[ht - 1]->link[0];
        }
        if ((!rPtr->link[0] || rPtr->link[0]->color == BLACK) &&
          (!rPtr->link[1] || rPtr->link[1]->color == BLACK)) {
          rPtr->color = RED;
        } else {
          if (!rPtr->link[0] || rPtr->link[0]->color == BLACK) {
            qPtr = rPtr->link[1];
            rPtr->color = RED;
            qPtr->color = BLACK;
            rPtr->link[1] = qPtr->link[0];
            qPtr->link[0] = rPtr;
            rPtr = stack[ht - 1]->link[0] = qPtr;
          }
          rPtr->color = stack[ht - 1]->color;
          stack[ht - 1]->color = BLACK;
          rPtr->link[0]->color = BLACK;
          stack[ht - 1]->link[0] = rPtr->link[1];
          rPtr->link[1] = stack[ht - 1];
          if (stack[ht - 1] == root) {
            root = rPtr;
          } else {
            stack[ht - 2]->link[dir[ht - 2]] = rPtr;
          }
          break;
        }
      }
      ht--;
    }
  }
}

// Print the inorder traversal of the tree
void inorderTraversal(struct rbNode *node) {
  if (node) {
    inorderTraversal(node->link[0]);
    printf("%d  ", node->data);
    inorderTraversal(node->link[1]);
  }
  return;
}

// Driver code
int main() {
  int ch, data;
  while (1) {
    printf("1\. Insertion\t2\. Deletion\n");
    printf("3\. Traverse\t4\. Exit");
    printf("\nEnter your choice:");
    scanf("%d", &ch);
    switch (ch) {
      case 1:
        printf("Enter the element to insert:");
        scanf("%d", &data);
        insertion(data);
        break;
      case 2:
        printf("Enter the element to delete:");
        scanf("%d", &data);
        deletion(data);
        break;
      case 3:
        inorderTraversal(root);
        printf("\n");
        break;
      case 4:
        exit(0);
      default:
        printf("Not available\n");
        break;
    }
    printf("\n");
  }
  return 0;
}

// Implementing Red-Black Tree in C++

#include <iostream>
using namespace std;

struct Node {
  int data;
  Node *parent;
  Node *left;
  Node *right;
  int color;
};

typedef Node *NodePtr;

class RedBlackTree {
   private:
  NodePtr root;
  NodePtr TNULL;

  void initializeNULLNode(NodePtr node, NodePtr parent) {
    node->data = 0;
    node->parent = parent;
    node->left = nullptr;
    node->right = nullptr;
    node->color = 0;
  }

  // Preorder
  void preOrderHelper(NodePtr node) {
    if (node != TNULL) {
      cout << node->data << " ";
      preOrderHelper(node->left);
      preOrderHelper(node->right);
    }
  }

  // Inorder
  void inOrderHelper(NodePtr node) {
    if (node != TNULL) {
      inOrderHelper(node->left);
      cout << node->data << " ";
      inOrderHelper(node->right);
    }
  }

  // Post order
  void postOrderHelper(NodePtr node) {
    if (node != TNULL) {
      postOrderHelper(node->left);
      postOrderHelper(node->right);
      cout << node->data << " ";
    }
  }

  NodePtr searchTreeHelper(NodePtr node, int key) {
    if (node == TNULL || key == node->data) {
      return node;
    }

    if (key < node->data) {
      return searchTreeHelper(node->left, key);
    }
    return searchTreeHelper(node->right, key);
  }

  // For balancing the tree after deletion
  void deleteFix(NodePtr x) {
    NodePtr s;
    while (x != root && x->color == 0) {
      if (x == x->parent->left) {
        s = x->parent->right;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          leftRotate(x->parent);
          s = x->parent->right;
        }

        if (s->left->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->right->color == 0) {
            s->left->color = 0;
            s->color = 1;
            rightRotate(s);
            s = x->parent->right;
          }

          s->color = x->parent->color;
          x->parent->color = 0;
          s->right->color = 0;
          leftRotate(x->parent);
          x = root;
        }
      } else {
        s = x->parent->left;
        if (s->color == 1) {
          s->color = 0;
          x->parent->color = 1;
          rightRotate(x->parent);
          s = x->parent->left;
        }

        if (s->right->color == 0 && s->right->color == 0) {
          s->color = 1;
          x = x->parent;
        } else {
          if (s->left->color == 0) {
            s->right->color = 0;
            s->color = 1;
            leftRotate(s);
            s = x->parent->left;
          }

          s->color = x->parent->color;
          x->parent->color = 0;
          s->left->color = 0;
          rightRotate(x->parent);
          x = root;
        }
      }
    }
    x->color = 0;
  }

  void rbTransplant(NodePtr u, NodePtr v) {
    if (u->parent == nullptr) {
      root = v;
    } else if (u == u->parent->left) {
      u->parent->left = v;
    } else {
      u->parent->right = v;
    }
    v->parent = u->parent;
  }

  void deleteNodeHelper(NodePtr node, int key) {
    NodePtr z = TNULL;
    NodePtr x, y;
    while (node != TNULL) {
      if (node->data == key) {
        z = node;
      }

      if (node->data <= key) {
        node = node->right;
      } else {
        node = node->left;
      }
    }

    if (z == TNULL) {
      cout << "Key not found in the tree" << endl;
      return;
    }

    y = z;
    int y_original_color = y->color;
    if (z->left == TNULL) {
      x = z->right;
      rbTransplant(z, z->right);
    } else if (z->right == TNULL) {
      x = z->left;
      rbTransplant(z, z->left);
    } else {
      y = minimum(z->right);
      y_original_color = y->color;
      x = y->right;
      if (y->parent == z) {
        x->parent = y;
      } else {
        rbTransplant(y, y->right);
        y->right = z->right;
        y->right->parent = y;
      }

      rbTransplant(z, y);
      y->left = z->left;
      y->left->parent = y;
      y->color = z->color;
    }
    delete z;
    if (y_original_color == 0) {
      deleteFix(x);
    }
  }

  // For balancing the tree after insertion
  void insertFix(NodePtr k) {
    NodePtr u;
    while (k->parent->color == 1) {
      if (k->parent == k->parent->parent->right) {
        u = k->parent->parent->left;
        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->left) {
            k = k->parent;
            rightRotate(k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          leftRotate(k->parent->parent);
        }
      } else {
        u = k->parent->parent->right;

        if (u->color == 1) {
          u->color = 0;
          k->parent->color = 0;
          k->parent->parent->color = 1;
          k = k->parent->parent;
        } else {
          if (k == k->parent->right) {
            k = k->parent;
            leftRotate(k);
          }
          k->parent->color = 0;
          k->parent->parent->color = 1;
          rightRotate(k->parent->parent);
        }
      }
      if (k == root) {
        break;
      }
    }
    root->color = 0;
  }

  void printHelper(NodePtr root, string indent, bool last) {
    if (root != TNULL) {
      cout << indent;
      if (last) {
        cout << "R----";
        indent += "   ";
      } else {
        cout << "L----";
        indent += "|  ";
      }

      string sColor = root->color ? "RED" : "BLACK";
      cout << root->data << "(" << sColor << ")" << endl;
      printHelper(root->left, indent, false);
      printHelper(root->right, indent, true);
    }
  }

   public:
  RedBlackTree() {
    TNULL = new Node;
    TNULL->color = 0;
    TNULL->left = nullptr;
    TNULL->right = nullptr;
    root = TNULL;
  }

  void preorder() {
    preOrderHelper(this->root);
  }

  void inorder() {
    inOrderHelper(this->root);
  }

  void postorder() {
    postOrderHelper(this->root);
  }

  NodePtr searchTree(int k) {
    return searchTreeHelper(this->root, k);
  }

  NodePtr minimum(NodePtr node) {
    while (node->left != TNULL) {
      node = node->left;
    }
    return node;
  }

  NodePtr maximum(NodePtr node) {
    while (node->right != TNULL) {
      node = node->right;
    }
    return node;
  }

  NodePtr successor(NodePtr x) {
    if (x->right != TNULL) {
      return minimum(x->right);
    }

    NodePtr y = x->parent;
    while (y != TNULL && x == y->right) {
      x = y;
      y = y->parent;
    }
    return y;
  }

  NodePtr predecessor(NodePtr x) {
    if (x->left != TNULL) {
      return maximum(x->left);
    }

    NodePtr y = x->parent;
    while (y != TNULL && x == y->left) {
      x = y;
      y = y->parent;
    }

    return y;
  }

  void leftRotate(NodePtr x) {
    NodePtr y = x->right;
    x->right = y->left;
    if (y->left != TNULL) {
      y->left->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->left) {
      x->parent->left = y;
    } else {
      x->parent->right = y;
    }
    y->left = x;
    x->parent = y;
  }

  void rightRotate(NodePtr x) {
    NodePtr y = x->left;
    x->left = y->right;
    if (y->right != TNULL) {
      y->right->parent = x;
    }
    y->parent = x->parent;
    if (x->parent == nullptr) {
      this->root = y;
    } else if (x == x->parent->right) {
      x->parent->right = y;
    } else {
      x->parent->left = y;
    }
    y->right = x;
    x->parent = y;
  }

  // Inserting a node
  void insert(int key) {
    NodePtr node = new Node;
    node->parent = nullptr;
    node->data = key;
    node->left = TNULL;
    node->right = TNULL;
    node->color = 1;

    NodePtr y = nullptr;
    NodePtr x = this->root;

    while (x != TNULL) {
      y = x;
      if (node->data < x->data) {
        x = x->left;
      } else {
        x = x->right;
      }
    }

    node->parent = y;
    if (y == nullptr) {
      root = node;
    } else if (node->data < y->data) {
      y->left = node;
    } else {
      y->right = node;
    }

    if (node->parent == nullptr) {
      node->color = 0;
      return;
    }

    if (node->parent->parent == nullptr) {
      return;
    }

    insertFix(node);
  }

  NodePtr getRoot() {
    return this->root;
  }

  void deleteNode(int data) {
    deleteNodeHelper(this->root, data);
  }

  void printTree() {
    if (root) {
      printHelper(this->root, "", true);
    }
  }
};

int main() {
  RedBlackTree bst;
  bst.insert(55);
  bst.insert(40);
  bst.insert(65);
  bst.insert(60);
  bst.insert(75);
  bst.insert(57);

  bst.printTree();
  cout << endl
     << "After deleting" << endl;
  bst.deleteNode(40);
  bst.printTree();
}

红黑树应用

  1. 实现有限图
  2. 要实现 Java 包：java.util.TreeMap和java.util.TreeSet
  3. 要在 C++ 中实现标准模板库（STL）：多集，映射，多映射
  4. 在 Linux 内核中