3.5.6 圆锥投影

圆锥投影

圆锥投影是以圆锥面为承影面的一类投影。假想用圆锥包裹着地球且与地球面相切(割)，将经纬网投影到圆锥面上，再将圆锥面展开为平面而成。
横轴和斜轴圆锥投影实际上很少应用，所以凡在地图上注明是圆锥投影的，一般都是正轴圆锥投影（兰勃特投影）。
由于地球上广大陆地位于中纬度地区，又因为圆锥投影经纬线网形状比较简单，所以被广泛应用于编制各种比例尺地图。

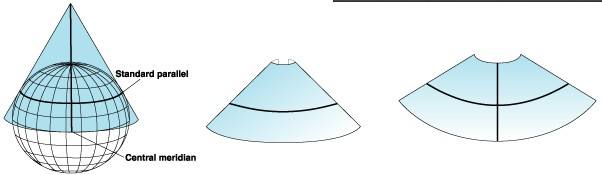
正轴圆锥投影特点如下

• 如将圆锥沿一线剪开展为平面，则成扇形，其顶角小于360°。
• 纬线表现为同心圆弧，且纬线之间平行。
• 经线表现为放射状的直线束，经线之间夹角和经差成正比，是同心圆弧的半径。
• 经纬线正交，且经纬线上的长度比为最大最小长度比。
• 变形大小随纬度变化，与经度无关，同纬线上的变形相等。
• 由于各类圆锥投影的变形性质不同，经线长度比不同，在图形上表现为纬线间隔的变化不一样。
• 等变形线与纬线平行呈同心圆弧分布。
• 以标准等变形线（标准纬线）和椭球的关系分为切和割两种情况。
• 在切圆锥投影上，相切的纬线是标准纬线，从标准纬线向南、北方向变形逐渐增大。标准纬线以北比标准纬线以南变形增加快。
• 在割圆锥投影上，相割的两条纬线是标准纬线，在两条标准纬线之间的纬线长度比小于1，两条标准纬线以外的纬线长段比大于1，离标准纬线愈远，变形愈大。

圆锥系数

圆锥系数c是指圆锥顶角与圆周角360度之比，其与圆锥的切、割位置等条件有关。
不同的圆锥投影具有不同的c，对一个具体的圆锥投影来说，c值固定。
方位投影和圆柱投影都是圆锥投影的特例。

• 0<c<1，圆锥投影。
• c=1，方位投影。
• c=0，圆柱投影。

圆锥投影分类

圆锥投影按变形性质可以分为等角、等积和任意三类投影，无论哪一种均有切与割之分。

• 正轴等角圆锥投影

使投影面上任一点的经线长度比与纬线长度比相等，即变形椭圆上长短半轴相等，就得到等角圆锥投影。

等角圆锥投影在全世界得到了广泛采用。我国1:100万基本比例尺地形图采取分带的边纬与中纬变形绝对值相等的双标准纬线兰勃特等角投影，每幅图单独进行投影。

• 正轴等积圆锥投影

使投影面上任一点的经线长度比与纬线长度比互为倒数，即变形椭圆上长短半轴成反比，就得到等积圆锥投影。

等积圆锥投影常用以编制行政区划图、人口密度图及社会经济地图等。