2.2.2 绝对精度指标

• 平均误差
  • 测量误差的平均，在一定观测条件下，一组观测值误差的算术平均值。
    测量误差的算术平均值不能反映偶然误差的离散程度，即测量误差平均值是反映准确度的指标。
    以下学习讨论中，涉及到精度这个概念，我们只讨论偶然误差影响，不考虑系统误差。
  • 偶然误差绝对值的平均，在一定观测条件下，一组观测值误差绝对值的算术平均值。
    不考虑系统误差的情况下，偶然误差绝对值的算术平均值用来评估精度是最简单的精度衡量方式，但偶然误差平均值不能很好地衡量误差的离散程度。
• 方差

在一定观测条件下，一组真误差平方的平均值叫方差，它度量了一组测量误差离散的程度。

当观测次数无穷大时，该组误差的离散度趋近最小。方差是误差正态分布曲线的拐点，方差的大小反映了误差函数离散程度。方差越小，代表一组观测值精度越高。

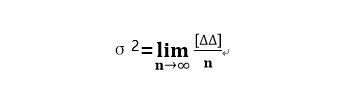
一般测量中，观测次数不可能无穷大，在n取值范围有限时，用改正数代替真误差来计算方差。改正数一般取观测值与观测值的算术平均值之差来求得，下式称为白塞尔公式。

由于对随机变量的测量，必要观测数为1，分母取多余观测数为（n-1）。相关内容参见（—-多余观测量章节）

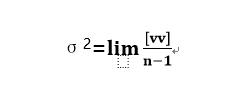
• 中误差

中误差为方差的平方根，在统计学里称作标准差，为了便于衡量精度大小，中误差恒取正值。

例题1
在某仪器检定场，某基线的长度是500m，为鉴定某台测距仪的精度，对该基线共观测了10次，得观测值为：500.010  499.992  499.998  500.005  499.987  500.002  500.009  499.999  499.993  500.003，该仪器的精度为多少？
解:
σ2=[∆∆]/n=506/10=50.6(mm2)  =>  σ=7.1(mm)
例题2
对某个距离共测量了10次，得观测值为（单位m）：500.010  499.992  499.998  500.005  499.987  500.002  500.009  499.999  499.993  500.003，则该组距离测量的中误差为多少？
解:
（课堂做）
解析（课堂说）
例题3
设在一个由n个三角形组成的三角锁中，以同精度观测了各三角形的三个内角，分别为Li1，Li2,，Li3; (i= 1，2，…，n)可得n个三角形的闭合差为w,求三内角和观测值的中误差。