1. 相关分析的适用情况
- 自变量和因变量均为数值型变量（定距与定比）
-例如学习时长与学习成绩之间的关系
- 有时定类和定序变量也可以看成数值型变量
-例如性别和对某明星喜爱度之间的关系
一般在进行相关分析前会先做散点图，观察基本情况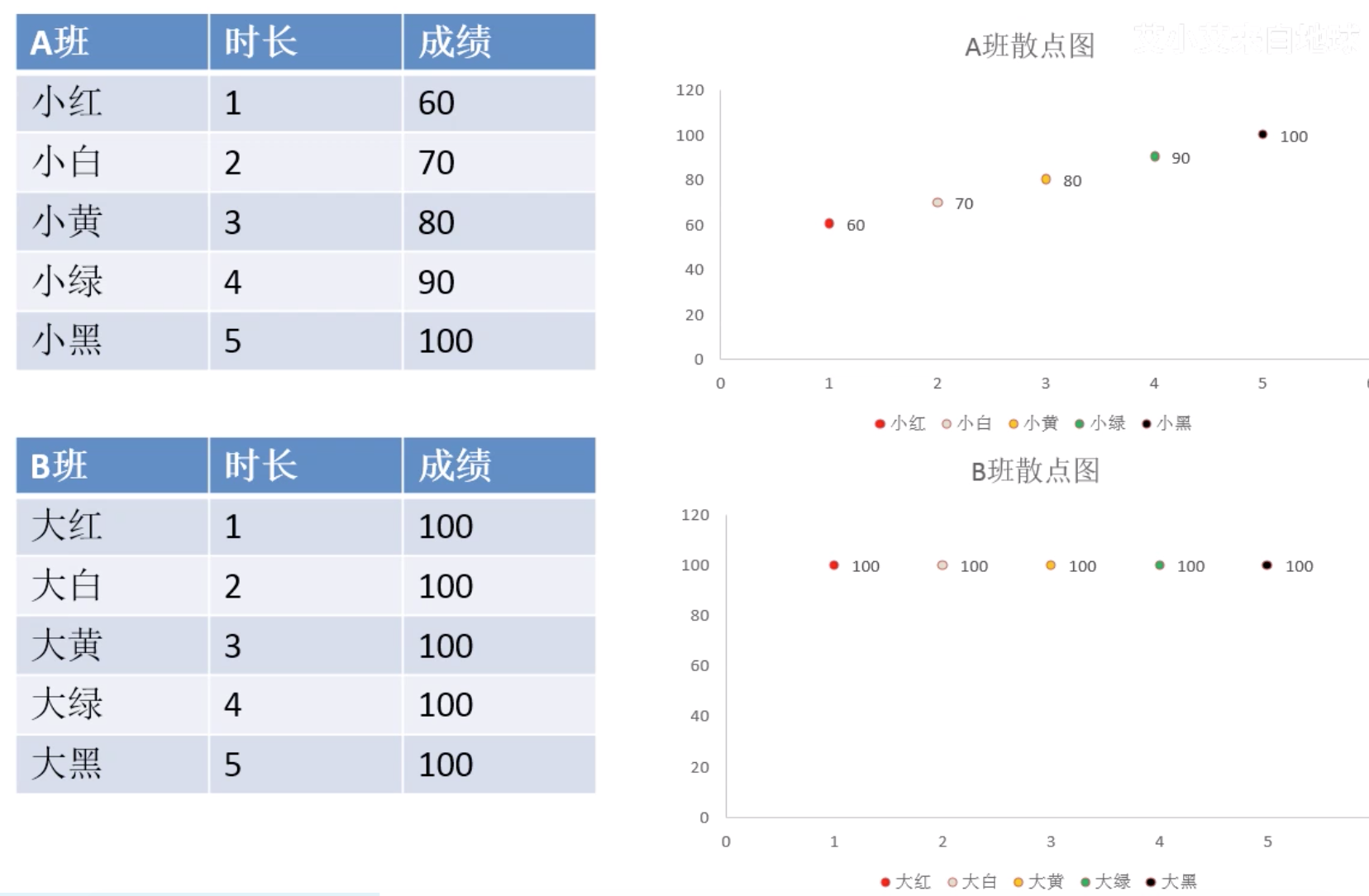
- 计算相关系数r
皮尔逊（Pearson）相关系数计算公式为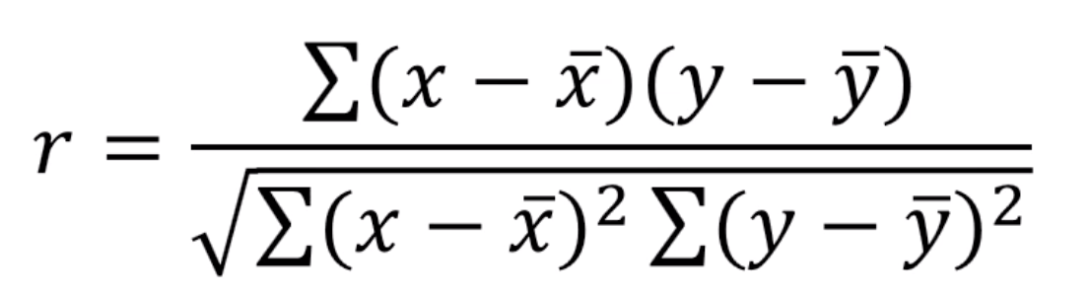
可以确定x与y之间相关性的强度和方向。
- -1 ≤ r ≤ 1，r的绝对值越接近1，相关性越强；越接近0，相关性越弱
- r > 0时为正相关；r < 0时为负相关
- r < 0.4时低度相关，r > 0.7时高度相关，0.4 ≤ r ≤ 0.7时中度相关
- 相关系数的检验，r符合t分布
H：ρ=0（ρ为总体的相关系数）
H：ρ≠0
r的比较分布为t分布，自由度df=n-2，标准误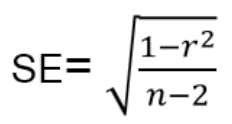
，t=r/SE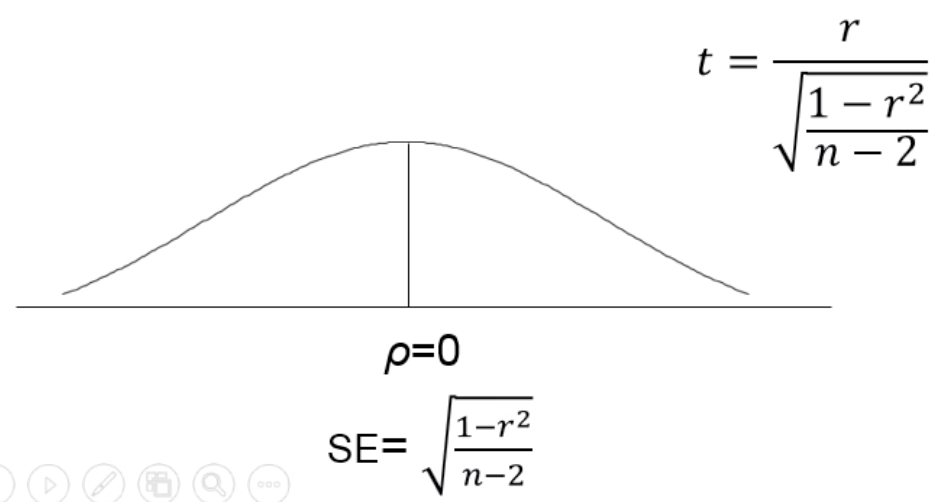
3. 案例
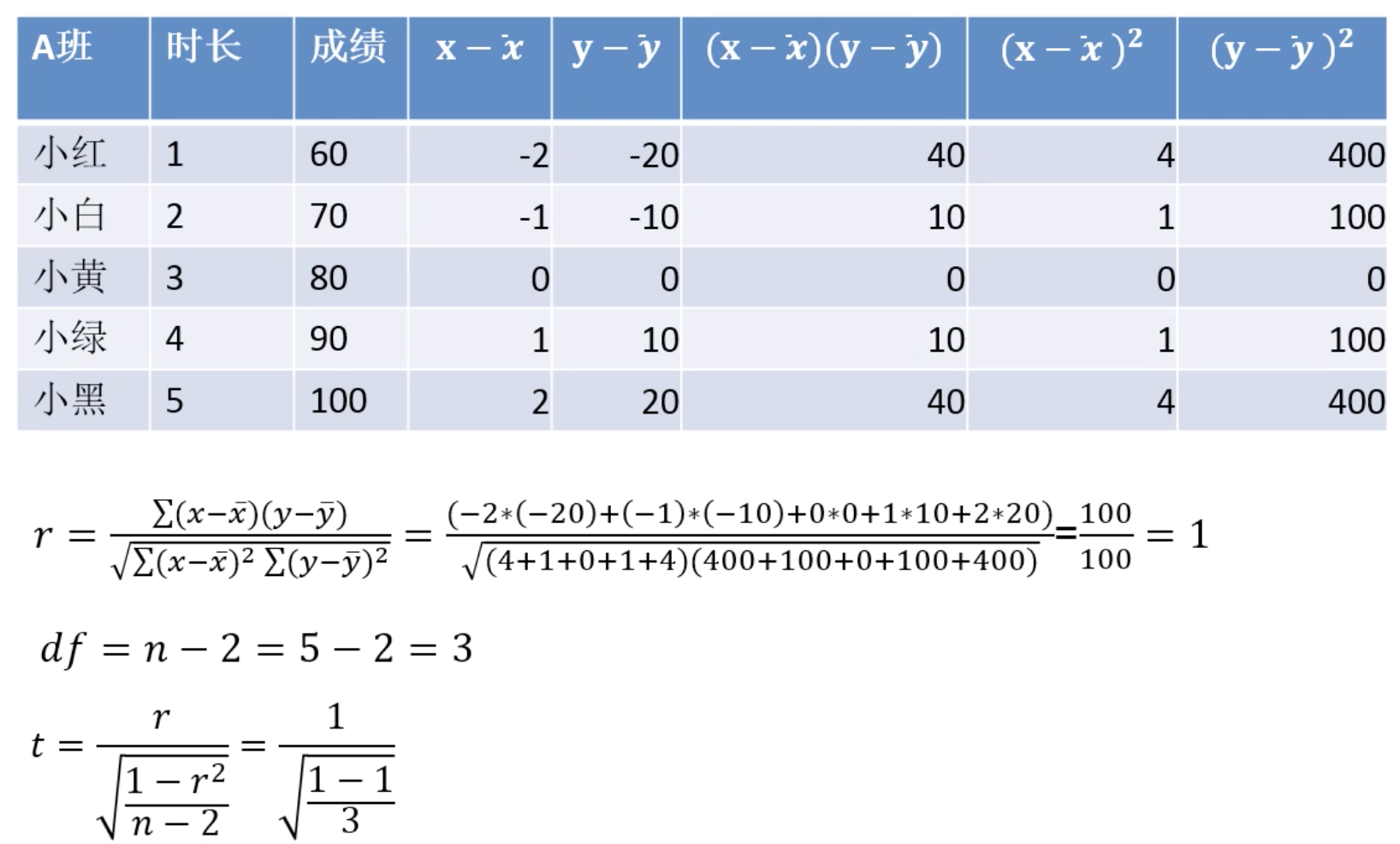
能否不计算t值就知道r是否统计意义上是否显著？
答案是：可以查表（如下图所示），只需知道r和df即可。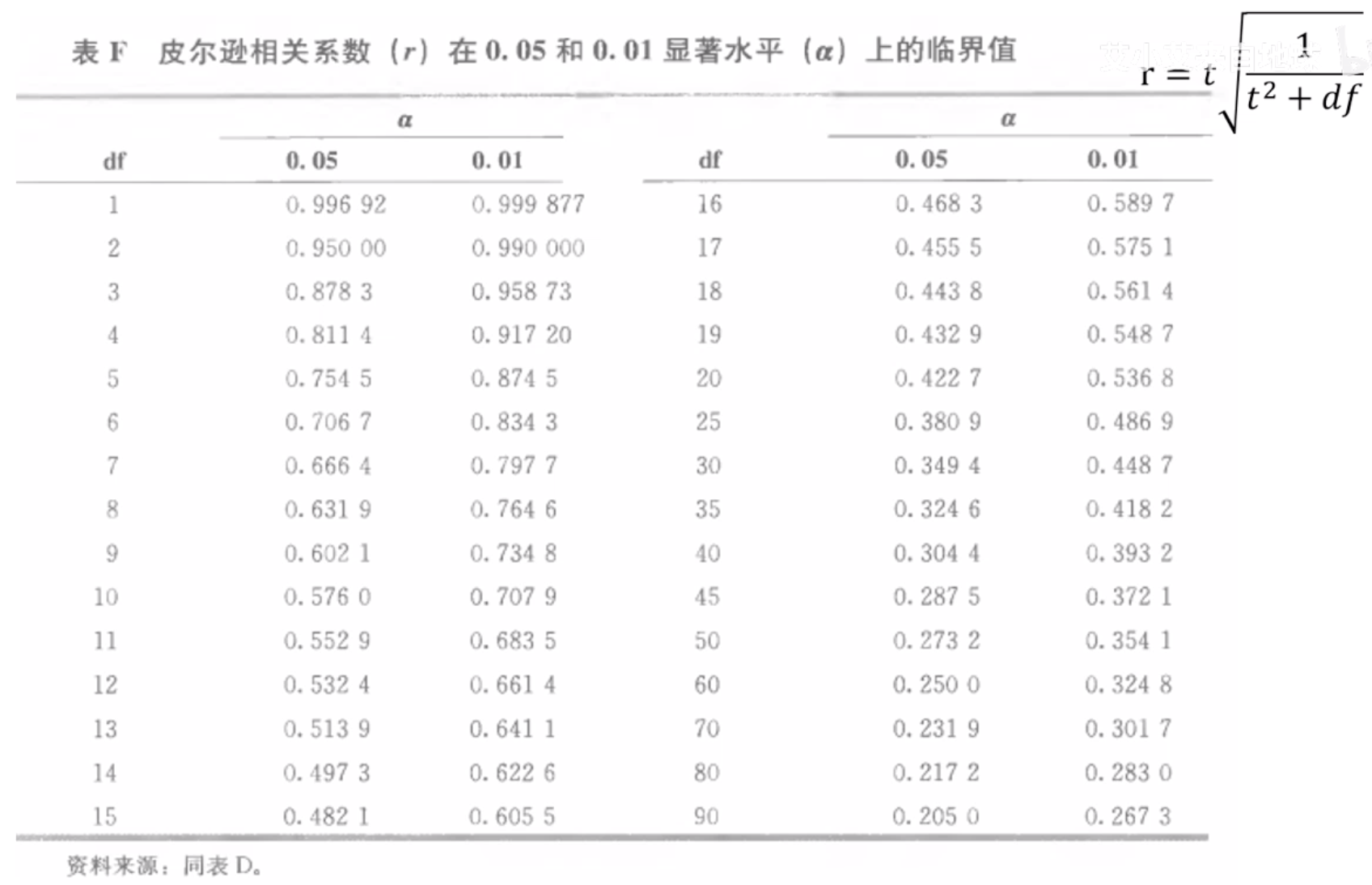
比如上述案例df=3，α=0.05时，临界值为0.8783，r ≥ 0.8783时，就具有显著的统计意义。
同时从表中也能观察到：df越大，临界值越小，r具有统计学意义所需的绝对值越小。**
若有收获，就点个赞吧
0 人点赞
