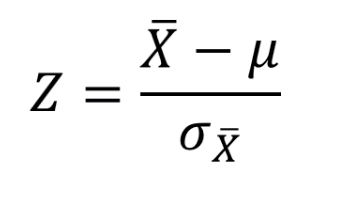6.1 样本、总体
1. 定义
总体:社会研究人员想试图了解的整个大群体。
样本:社会研究者通过抽样所调查的一个小群体。
2. 抽样方法
- 非随机抽样
- 方便抽样
- 配额抽样
- 判断抽样
- 随机抽样
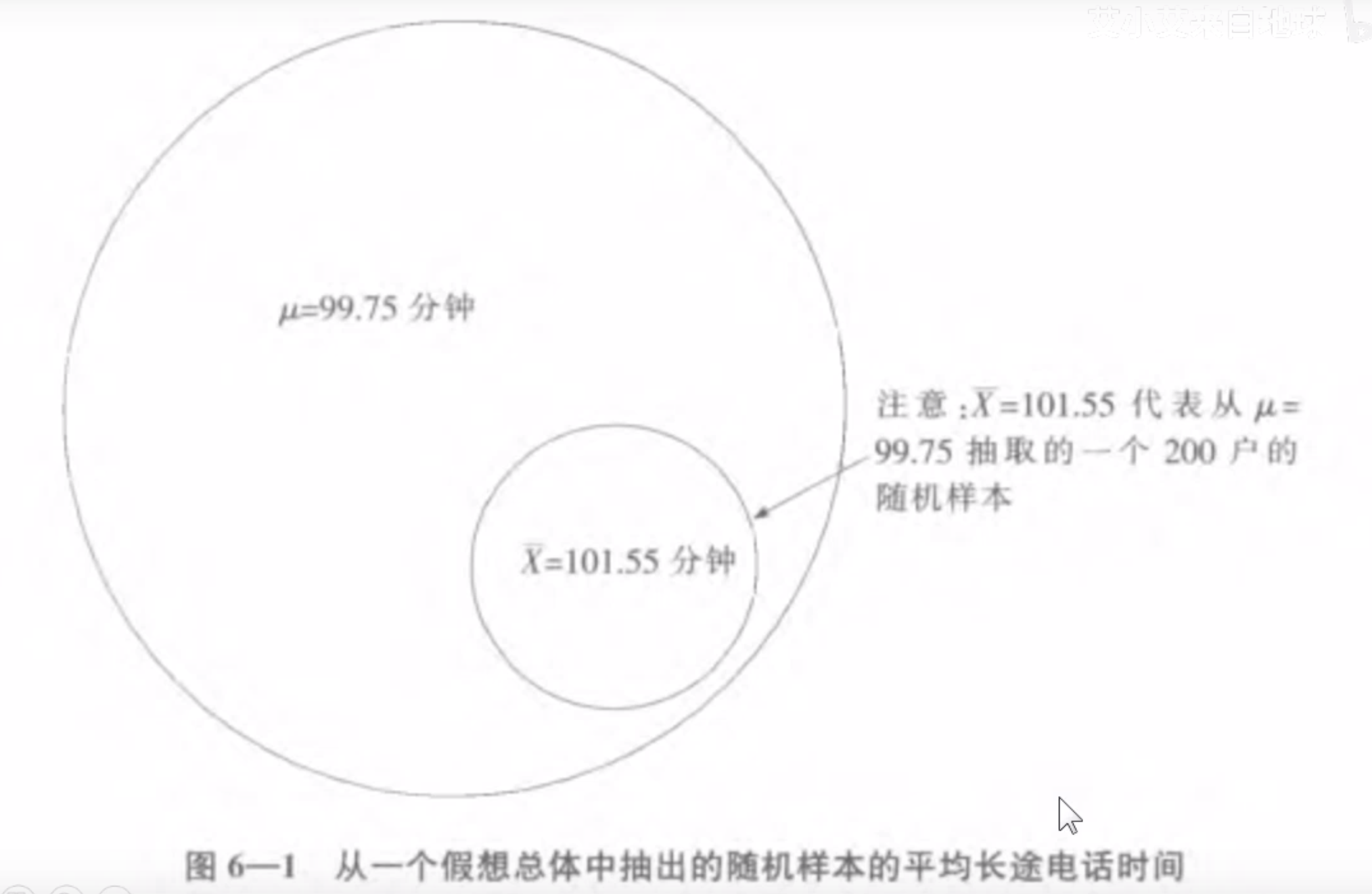
6.2 均值的抽样分布
1. 均值的抽样分布的特性
- 均值的抽样分布近似于正态分布。这一点对于所有的抽样分布的均值都成立,不论其总体的原始数据的分布形状是什么,而只要样本足够大(大于30)。
- 均值的抽样分布的均值(均值的均值)与真实的总体均值相等。
- 均值的抽样分布的标准差比总体的标准差要小。即样本均值更加稳定。
2. 标准误
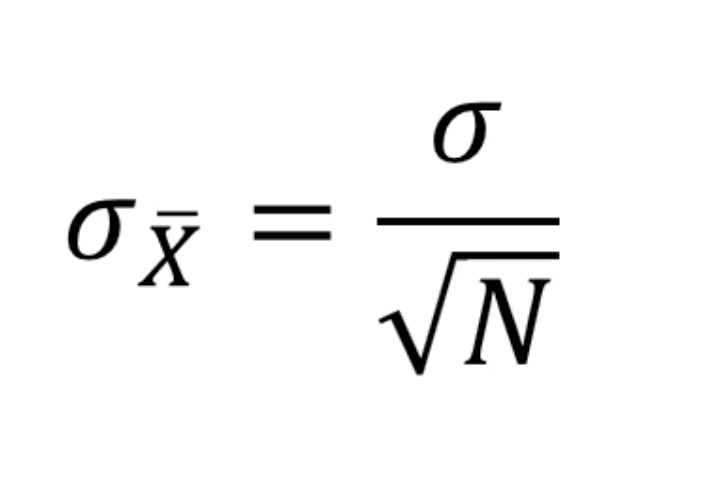
σx̅:均值抽样分布的标准误
σ:总体的标准差
N:抽样分布的样本数量
例如,标准化的智商测验的总体均值( μ )为100,总体标准差(σ)为15。如果抽取一个规模为10的样本,样本均 值的标准误将会是?> 解答:σ> x̅=>

3. Z值
x̅:某一样本的均值
v:总体均值
σx̅:均值的抽样分布的标准误 例如,标准化的智商测验的总体均值( μ )为100,总体标准差(σ)为15。如果抽取一个规模为10的样本,均值为105,请问样本均值的Z分数是多少?抽中样本均值等于或高于这个智商的概率是多少? 解答: 1)求抽样样本均值的标准误:σx̅=2)求Z分数:Z=(x̅-μ)/σx̅=(105-100)/4.74=1.05 3)根据Z值查表得P值为0.15
6.3 置信区间
1. 定义
由样本估计量构造出的总体参数在一定置信水平下的估计区间,称为置信区间(Confidence Interval, CI)。
例:假设一所私立中学的校长想要估计学生的平均智商,而又不想花费时间和精力在对1000名学生进行的测验上。因此,这位校长随机抽取了25名学生进行测试。他发现他的样本均值为105。( 假设总体标准差已知为σ=15)
解答:
1)样本均值的标准误:σx̅=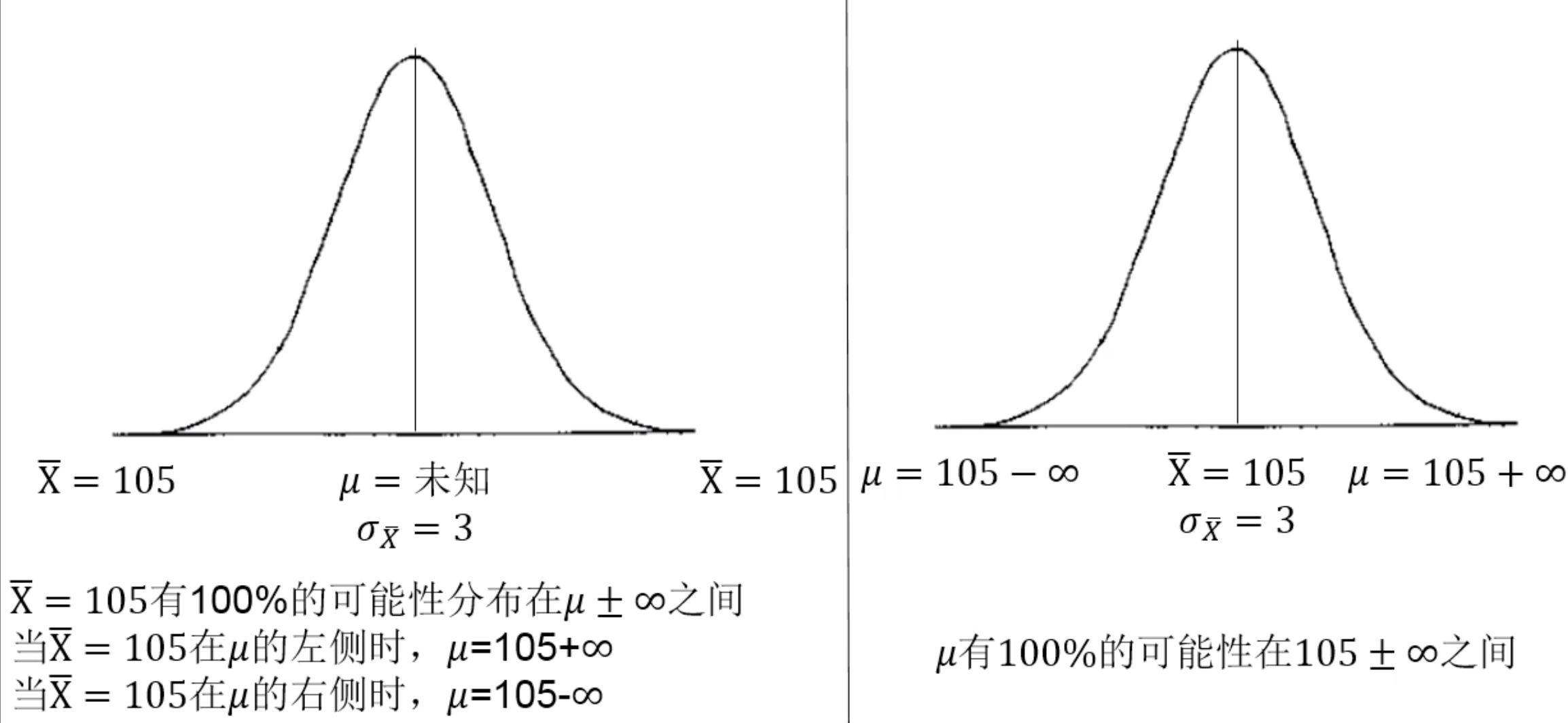
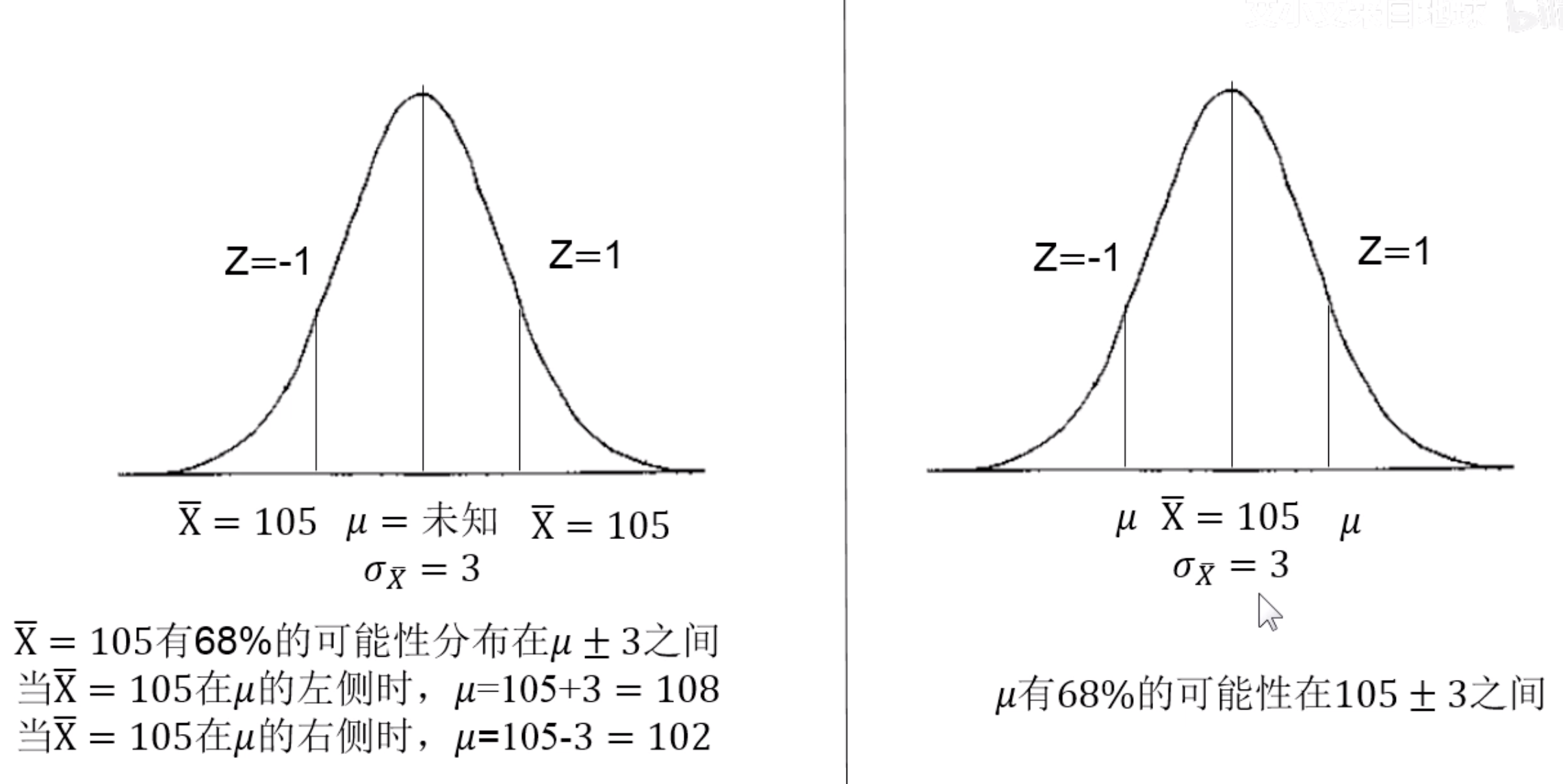
- 因此,这位校长可以以68%的置信度得出结论,全校的平均智商(μ)为105±3。
- 换句话说,有68%的机会(p=0.68),真实的总体均值在102-108这个区间内,即置信区间。
- 在一个特定的概率水平(如68%)上有±3的误差范围,或者叫做估计误差。
一般在研究问题时,构建的是在95%置信水平的置信区间。95%叫置信度、置信水平、置信系数,或表示为α=0.05的显著性水平。
上述例题若使用95%的置信度,则如下所示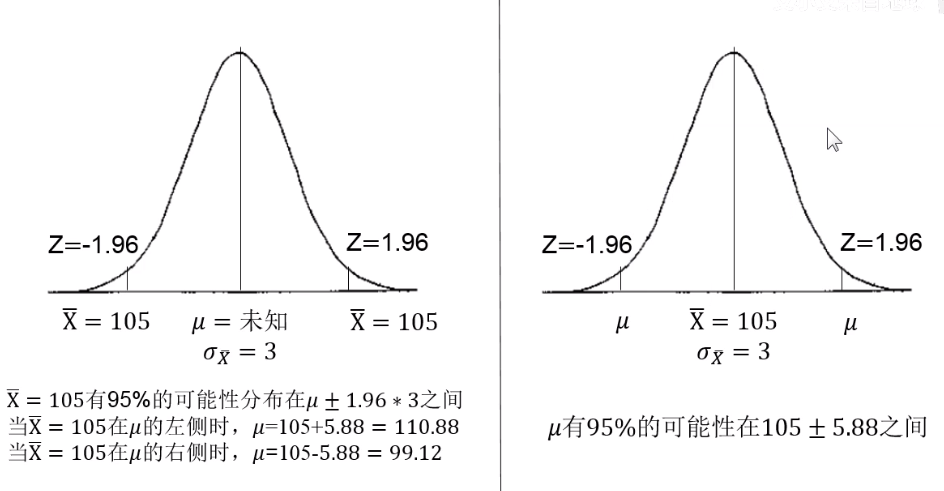
95%的置信区间= x̅ ± Z σx̅ = 105 ± 1.96 3 = 105 ± 5.88 = 99.12~110.88
其中5.88为估计误差
**
2. 常用的置信水平及对应的Z值(需记住)
| 置信度 | Z值 |
|---|---|
| 90% | 1.64 |
| 95% | 1.96 |
| 99% | 2.58 |
3. 对置信区间的理解
- 总体均值是固定的,而样本构造出的置信区间是不固定的,是一个随机区间,会因样本的不同而不同。
- 95%的置信区间意味着假设从总体中抽取100个样本构造置信区间,其中有95个包含了真实的总体参数,有5个没有包含。
- 总体均值的置信区间 = 样本均值 ± 误差范围(又叫估计误差),估计误差 = Z σx̅ = Z σ/√N。因此在总体方差已知的情况下,若要减小估计误差,可以1)设置一个小的置信水平或2)增大样本量。
6.4 均值的标准误(总体的标准差未知)
在6.3中计算总体均值的置信区间,有个前提是“总体方差已知”。如果现在不知道总体方差,该怎么办呢?
点击查看【bilibili】
1. 无偏估计
1)如果不知道总体标准差σ,则需要根据样本信息对总体的标准差进行无偏估计
2)在均值的抽样分布中,依据 对均值的标准误进行无偏估计
对均值的标准误进行无偏估计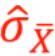


但在有的教材中,均值标准误的无偏估计写作Sx̅=
这是因为他们在计算样本的标准差S时,使用的公式为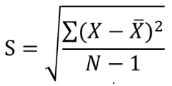 。计算样本标准差时,如果分母是N-1,说明是希望想通过样本求总体标准差;如果分母是N时,说明只是计算样本的标准差。目的不同,导致过程不同,但最终计算均值的标准误的无偏估计时,结果是相同的。
。计算样本标准差时,如果分母是N-1,说明是希望想通过样本求总体标准差;如果分母是N时,说明只是计算样本的标准差。目的不同,导致过程不同,但最终计算均值的标准误的无偏估计时,结果是相同的。
2. 标准误
如果总体标准差未知,均值的抽样分布服从于自由度为N-1的t分布,其均值为总体均值μ,标准误为
Sx̅=
自由度:以样本的统计量来估计总体参数时,样本中能自由变换的数据个数。
例如:在N=3的X、X、X的样本中,已知均值x̅=10,那么X、X两个数可以随便取值,但因为均值固定了,所以X值就是固定的,因此该样本的自由度df=3-1=2。
3. t分布
t分布是英国统计学家W.S.Gosset在1908年以笔名Student发表的论文中提出的,因此又叫学生t分布。
t分布的特性
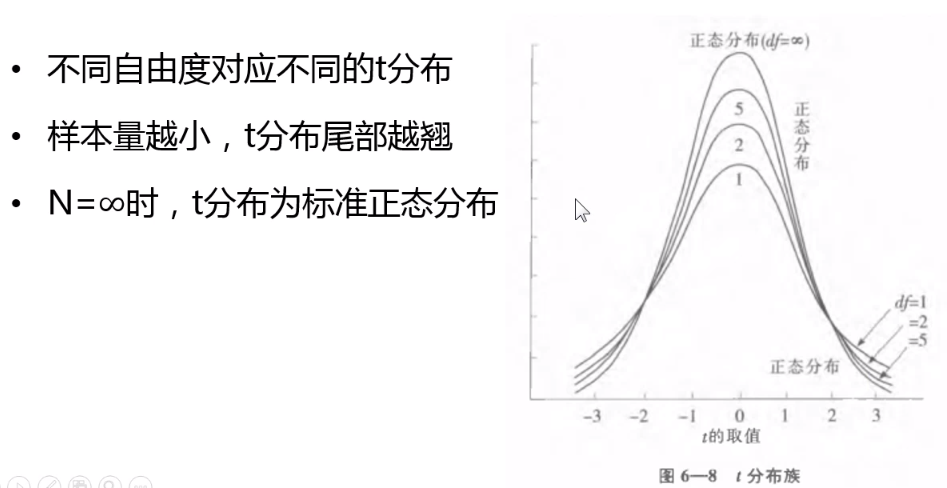
t分布查表,根据显著性水平和自由度查表,得到t值。
比α=5%,N=6,则自由度df=5,对应的t值为2.571。
利用t值计算置信区间
通过逐步演示,让我们看一下如何利用t值计算置信区间。假设有一位研究人员想要检验幼儿园的儿童的合作程度。为了达到这个目的,他无参与地观察了一组儿童玩耍30分钟并记录下每一个儿童所采取的合作行为的次数。下面是每一个儿童所表现的合作行为的数量x:1、5、2、3、4、1、2、2、4、3
- 计算样本的均值x̅
x̅=ΣX/N
=(1+5+2+3+4+1+2+2+4+3)/10
=2.7
- 计算样本标准差s
s=1.2689
- 计算均值的标准误的估计值Sx̅
Sx̅=
=1.2689/3
=0.423
- 查表求t值
α=0.05,df=10-1=9
查表得t=2.262
- 求误差范围
误差范围= t Sx̅ = 2.262 0.423 = 0.96
- 求置信区间
95%的置信区间 = 样本均值 ± 误差范围 = 2.7 ± 0.96 = 1.74~3.66
6.5 总体比例π的置信区间
1. 总体比例π
例:假如东华大学对学生的一次普查(假如总人数为10000人)。得知有65%的学生赞成“取消四六级考试”,有35%不赞成或不表示意见。在调查中,对”赞成”的学生给予1的值,否则给予0的值。
求总体中”赞成”的比例π、总体均值、总体方差
| 赞成与否 | 人数 | 百分比 |
|---|---|---|
| 1 | 6500 | 65% |
| 0 | 3500 | 35% |

总结规律:
当总体的取值只有0和1两种情况时,取1的比例为π,则
- 总体均值μ=总体的比例π
- 总体方差σ2=π(1-π)
- 总体标准差
2. 样本比例P
当随机地抽取10位学生进行调查时,得到样本值为1,0,0,1,1,1,0,1,1,1。
求样本中”赞成”的比例、样本的均值、方差、标准差。
| 赞成与否 | 人数 | 百分比 |
|---|---|---|
| 1 | 7 | 70% |
| 0 | 3 | 30% |
- 样本中“赞成”的比例P=7/10=0.7
- 样本的均值**x̅=(17+03)/10=0.7,因此可知**x̅=P
3. 比例的标准误S


4. 比例的抽样分布
- 比例的抽样分布近似正态分布
- 均值为总体比例π,标准误为S
- 用样本比例P去估算π的95%的置信区间=P±1.96S=
拓展:Z分布中,置信度与对应的Z值 95%对应1.9690%对应1.64
例:假设本地的一家调查组织通过电话联系了400名本地的登记选民,询问他们倾向于投票给候选人A还是B。
假设有60%报告他们将投票给候选人A。现在让我们从标准误、误差范围和比例的95%置信区间来说明对候选人A的倾向。
分析:如果95%的置信区间内的支持率都在50%以上,也就是置信区间最小值都高于50%,则说明A当选。
解答:
- 计算比例的标准误S
- 计算误差范围1.96S
- 样本比例加减误差范围来计算置信区间
95%置信区间==0.552~0.648
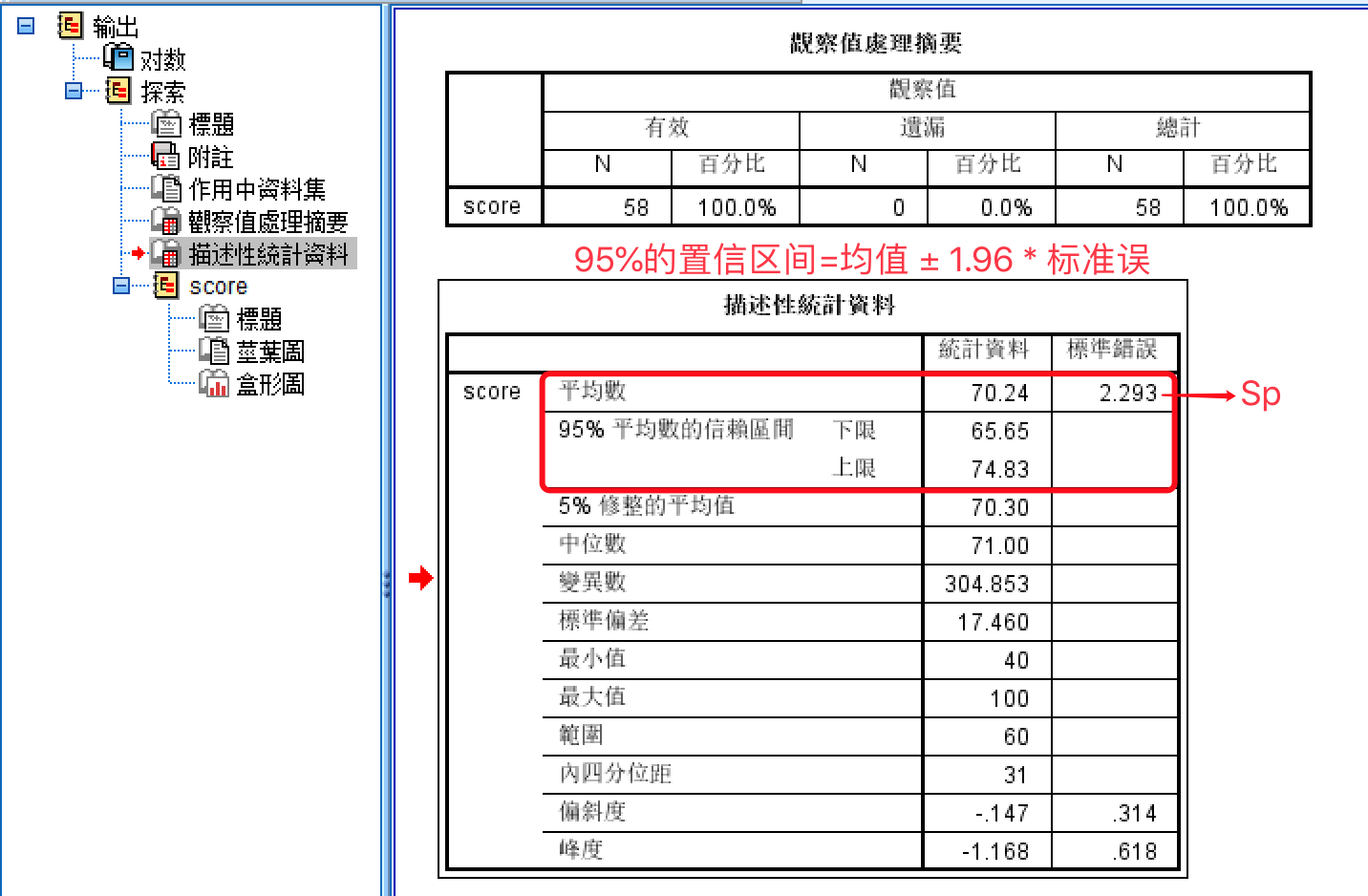
6.6 用spss看置信区间与标准误
分析-描述统计-探索-选择因变量-statics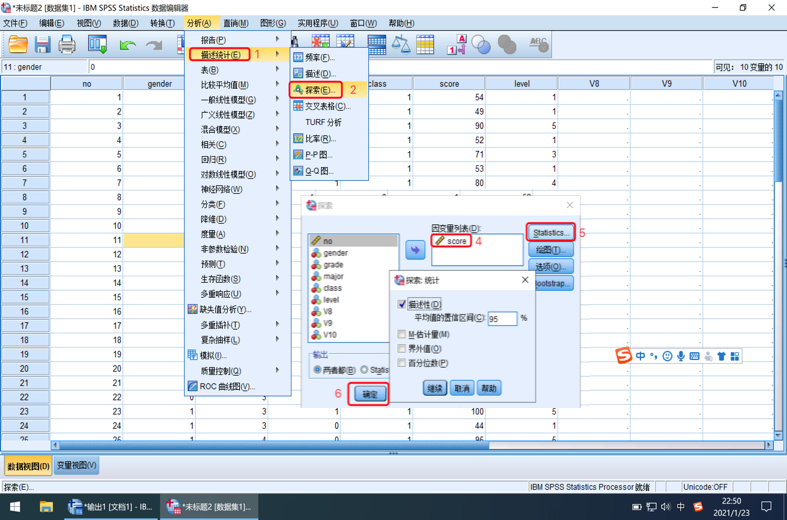
结果如下所示