6.9 贝叶斯

点击查看【bilibili】

贝叶斯公式推导

已知：如果某种疾病的发病率为千分之一。现在有一种试纸，它在患者得病的情况下，有99%的准确率判断患者得病，在患者没得病的情况下，有5%的可能误判患者得病。
问：现在试纸说一个患者得了病，那么患者真的得病的概率是多少？

解：设患病为事件A1，未患病为事件A2，测出有病为事件B。画出分析图 测出得病且真得病的概率：
P(患病 | 测出有病)
=P(患病)P(测出有病 | 患病) / (P(患病)P(测出有病 | 患病) + P(未患病)P(测出有病 | 未患病)
=99/(4559+99)
=1.9%
即：
P(A1|B)=P(A1)P(B|A1)/(P(A1)P(B|A1) + P(A2)P(B|A2))
P(A1|B)表示测出有病条件下患病的概率
P(A1)表示患病的概率，0.1%
P(A2)表示未患病的概率，99.9%

P(B|A1)表示患病的条件下测出有病的概率，99%
P(B|A2)表示未患病的条件下测出有病的概率，5%

推广到一般形式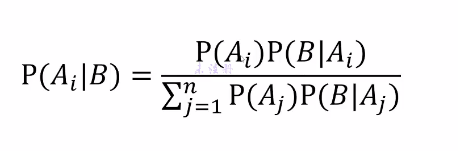

贝叶斯公式的意义

已经发生了某一结果，去计算某种原因导致该结果发生的概率，即从结果推导原因。

练习

1. 参加营销活动的人群中，女性只有30%，能否说明妹子们不爱参加此活动？

分析：
判断女性是否喜爱参加此活动，应该看”参加的女性/营销活动触达的所有女性”，这两个数据是未知的。已经条件的30%是指参加活动中的男女比例是7:3。

画图拆解问题 利用贝叶斯公式得
P(不参加 | 女性)
=P(不参加)P(女性 | 不参加) / (P(不参加)P(女性 | 不参加) + P(参加)P(女性 | 参加))

上式中，除了已知P(女性 | 参加))=30%，其他都是未知的，所以无法计算，因此不能给出“妹子们不爱参加此活动”的结论。

1. 腾讯校招题目

   （原题目取自诺比尔经济学者得主丹尼尔·卡尼曼《思考，快与慢》，点击查看关于贝叶斯定理简介）

某城市有两种颜色的出租车，蓝色和绿车市场比率15:85。一辆出租车夜间肇事后逃逸，但还好当时有一位目击证人，这位目击者认定肇事的出租车是蓝色的。但是，他的目击未必可信，公安人员经过在相同环境下对他进行“蓝绿”测试而得到：80%的情况下识别正确，20%的情况下识别错误。那么实际为蓝车的可能性是多少？

分析：

• 颜色分为蓝色、绿色两种情况，识别有正确、错误两种结果。
• 已知蓝色、绿色的占比和识别正误率。
• 要求的是：在识别正确的前提下，是蓝色的概率

画图拆解问题 根据贝叶斯公式得：
P(蓝色 | 识别为蓝色)
=P(蓝色)P(识别为蓝色 | 蓝色)/(P(蓝色)P(识别为蓝色 | 蓝色) + P(绿色)P(识别为蓝色 | 绿色))
=15% x 80% / (15% x 80% + 85% x 20%)
=41%

1. 我们经常会收到垃圾短信，假设在1000条正常短信中，包含“澳门赌场”的短信有2条，而在垃圾短信中，包含“澳门赌场”的短信有400条。现在我们接受到一条新短信，在不浏览内容的情况下，假定它是正常短信的概率是50%。现在对短信内容的解析，发现了“澳门赌场”这个词，那么它是垃圾短信的概率有多高？

解析：

• 收到垃圾短信（记为事件A），P(A)=1-P(正常短信)=50%
• 在收到垃圾短信的条件下，包含“澳门赌场”，记为条件事件B|A，P(B | A)=400/1000=40%
• 在收到正常短信的条件下，包含“澳门赌场”，记为条件事件B|A，P(B | A)=2/1000=0.2%
• 求：收到的短信包含“澳门赌场”的条件下，是垃圾短信的概率，记为P(A | B)

根据贝叶斯定理
P(A | B)
=P(A)P(B | A)/(P(B | A)P(A)+P(B | A)P(A))
=50%40%/(50%40+50%*0.2%)
=1%

贝叶斯的应用

在人工智能机器算法广泛应用