再好的技巧也需要建立在能够将问题回答得很好的基础上,本节对面试问题进行了汇总。 摘自《数据分析师求职面试指南》
一、基础知识考查
概率论与数理统计:
- 用简洁的话语阐述随机变量的含义。
在介绍随机变量之前,首先需要说下随机试验的概念,随机试验是指在相同条件下对某随机现象进行的大量重复试验。而“随机变量”这个概念的引入就是为了描述随机试验的结果的,通常用大写的X来表示。
- 划分连续型随机变量和离散型随机变量的依据。
二者的区别在于所描述的随机试验所有可能的结果数量是否可数。
(注意是“是否可数”,不是“是否有限”。类似于有理数与无理数的关系。)
- 常见分布的分布函数/概率密度函数,以及分布的特性,如指数分布的无记忆性。
**
| 分类 | 名称 | 特性 | 应用举例 |
|---|---|---|---|
| 离散型随机变量分布函数 | 0—1分布(伯努利分布) Pr(x=1)=p, Pr(x=0)=1-p |
非A即B,只有0、1两种结果。 | 抛硬币 |
| 二项分布(N重伯努利分布) Pr(X=x)=P(1-p) |
每个事件发生的概率相同; 各个试验的结果相互独立。 |
发放优惠券,被使用的概率 | |
| 泊松分布 Pr(X=x)=e**-λ*λk/k!** |
适用描述单位时间(或空间)内随机事件发生的次数。 | 网站或APP在一定时间内访问的人数 | |
| 连续型随机变量概率密度函数 | 均匀分布 f(x)=1/(b-a),x∈[a,b] |
概率密度函数在结果去见内为固定数值的分布。 | 公交车平均30分钟发一次车,每次等车时间x为5~15分钟的概率为f(x)=∫155 1/(30-0)=1/3 |
正态分布 |
所有的分布随着数据量的增加,其均值的分布都会逼近正态分布(中心极限定理) | 数据质量监控中的3σ方法。 |
正态分布中,
- 至少68%的数据位于平均数1个标准差范围内;
- 至少95%的数据位于平均数2个标准差范围内;
- 至少99.8的数据位于平均数3个标准差范围内。
切比雪夫定理,一组数据
- 至少有75%的数据,位于平均数2个标准差范围内
- 至少有89%的数据,位于平均数3个标准差范围内
- 至少有96%的数据,位于平均数5个标准差范围内
|
| | 指数分布
f(x)=λeλx | 描述泊松过程中事件之间的时间的概率密度,即事件以恒定的平均速率连续且独立发生的过程。
特点是无记忆性 | |
- 随机变量常用特征的解释(期望、方差等)。
- 期望:用来表示随机变量X的平均水平。随着试验次数的增加,X的均值愈发趋近于期望值。
- 方差&标准差:用来刻画随机变量X的波动大小。得到期望和标准差后,可标准化变量X’=(X-μ)/σ。
- 分位数:对于随机变量X,除了要关注它的期望和方差,还要关注它的某个样本x在整体分布中的排序情况。若Pr ( X≤t)=α,则将t称为X的α分位数。若α等于0.5,则将t称为随机变量X的中位数。中位数是一种特殊的分位数。有了分位数,就可以更进一步地理解随机变量X,得到X在10%,20%,…,90%这些分位数对应的数值情况。
- 协方差&相关系数:协方差通常记为Cov(X,Y),Cov(X,Y) = E(X-E(X))(Y-E(Y))。
协方差分步计算方法:
设A列是x值,B列是y值,行数为n
1. 求X和Y的平均值X'和Y'1. C列=x-X',D列=y-Y'1. E列=(x-X平)(y-Y平)1. 协方差=E列求和/n
excel有直接的公式:covariance.p(总体)covariance.s(样本)
- 中位数是否等于期望。

答案是不一定。在不同的分布中,中位数、期望(均值)、众数三者的大小关系:
- 正态分布:中位数=期望=众数。
- 正偏态分布(右偏,图形尾巴在右侧):期望>中位数>众数。
- 负偏态分布(左偏,图形尾巴在左侧):期望<中位数<众数
记忆技巧:期望离尾巴近,中位数在中间,剩下的位置就是众数。
- 常见分布的特征值。
- 离散型随机变量分布函数的特征值

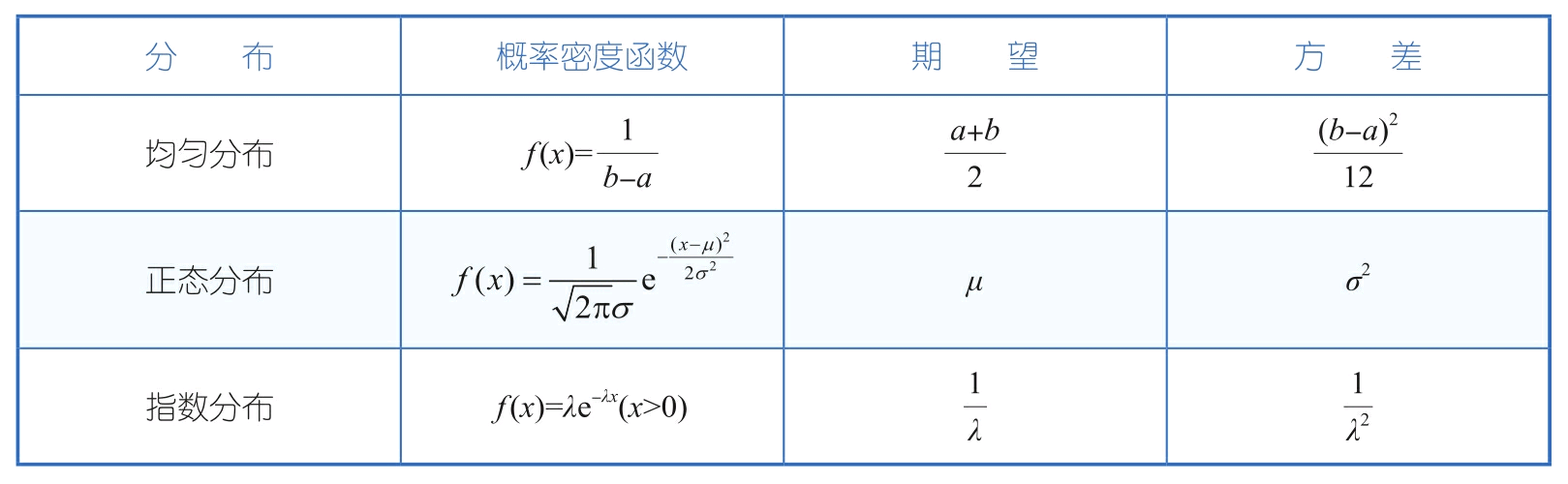
- 连续型随机变量概率密度函数的特征值
- 随机变量X+Y、XY的期望与X、Y期望的关系?
对于任意两个随机变量X、Y,都满足E(X+Y)=E(X) + E(Y);
对于两个相互独立变量X、Y,才满足E(XY) = E(X)E(Y)
反之,若E(XY) = E(X)E(Y),只能表明X和Y是不相关的,不能说明二者是相互独立的。
不相关和独立的关系和区别是:
独立一定不相关,不相关不一定独立。
相关和不相关换句话说是:线性相关和线性不相关;
独立换句话说是:没有任何关系(这个关系包括线性和非线性关系);
X,Y不相关指的是:X,Y两个变量线性不相关(即不存在线性关系,但可能存在非线性关系);
X,Y独立指的是:X,Y两个变量没有任何关系(即没有线性关系,也没有非线性关系)。
相关但不独立的例子:
设y=x,x与y之间会呈现明显的线性关系,但是x与y之间不存在线性关系,相关系数的绝对值接近于0,但是不能说二者是独立的。通过这个例子可以加深对变量独立与变量不相关区别的理解,二者实际上是一种包含关系。
- 如何给没有学过统计学的人解释正态分布。
**
- 列举常用的大数定律及其区别。

- 阐述中心极限定理和正态分布的直接关系。
设X,X,…,X,…是一组独立同分布的随机变量,E(X=μ,D(X)=σ(i=1,2,3,…),当n足够大时,均值的分布接近于正态分布N (μ,σ/n),将X进行标准化处理,就可以得到X’=(X平-μ)/(σ/)接近于N(0, 1)的标准正态分布。
- 如何利用编程语言设计实验证明中心极限定理。
**
- 简单阐述假设检验的原理。
通俗地讲就是:通过证明在原假设成立的前提下,检验统计量出现当前值或更为极端的值属于“小概率”事件,以此推翻原假设,接受备择假设。
上面是比较通俗的阐述,下面将其理论化。“检验统计量出现当前值或者更为极端的值”的概率就是常用的p-value;“小概率”的定义是将p-value与预先设定的显著性水平α进行对比,如果p-value小于α,就可以推翻原假设。因此,更为严谨的阐述应该是:通过证明该样本对应的p-value小于α,以此推翻原假设,接受备择假设。
- 在假设检验中原假设和备择假设选择的依据。
原假设和备择假设的选择是基于实际的需求,一般来说备择假设是我们真正需要关心和证明的内容,记为H,原假设则是备择假设的对立面,记为H。
- 阐述假设检验的两类错误。
第一类错误是指在原假设成立的情况下错误地拒绝了原假设;第二类错误则相反,指没有成功地拒绝不成立的原假设。
- 用通俗的语言解释p-value、显著性水平、检验效能。
p-value:在原假设成立的前提下,检验统计量出现当前值或者更为极端的值的概率。
显著性水平:在假设检验的过程中,通常会预先设定犯第一类错误的上限,也就是定义显著性水平α。通常会将α设定为5%,在一些要求比较严格的检验中,也会设定为1%,这取决于业务的实际要求。
置信度:1-α被称为置信度。
检验效能:在显著性水平固定的情况下,需要减少第二类错误β发生的概率。1-β对应于规避第二类错误的概率,用power表示,也称为检验效能。power的大小可以通过增加样本量来提高,通常需要power达到80%或者更高的水平。
- 分别解释z检验和t检验。
**
- 贝叶斯派统计和频率派统计的区别。
在频率派的观点中,样本所属的分布参数θ虽然是未知的,但是固定的,可以通过样本对θ进行预估得到 ˆθ。
贝叶斯派则认为参数θ是一个随机变量,不是一个固定的值,在样本产生前,会基于经验或者其他方法对θ预先设定一个分布π(θ),称为“先验分布”。之后会结合所产生的样本,对θ的分布进行调整、修正,记为π(θ|x1,x2,x3,…),称为“后验分布”。
频率学派和贝叶斯学派最大的差别其实产生于对参数空间的认知上。所谓参数空间,就是你关心的那个参数可能的取值范围。频率学派(其实就是当年的Fisher)并不关心参数空间的所有细节,他们相信数据都是在这个空间里的”某个“参数值下产生的(虽然你不知道那个值是啥),所以他们的方法论一开始就是从“哪个值最有可能是真实值”这个角度出发的。于是就有了最大似然(maximum likelihood)以及置信区间(confidence interval)这样的东西,你从名字就可以看出来他们关心的就是我有多大把握去圈出那个唯一的真实参数。而贝叶斯学派恰恰相反,他们关心参数空间里的每一个值,因为他们觉得我们又没有上帝视角,怎么可能知道哪个值是真的呢?所以参数空间里的每个值都有可能是真实模型使用的值,区别只是概率不同而已。于是他们才会引入先验分布(prior distribution)和后验分布(posterior distribution)这样的概念来设法找出参数空间上的每个值的概率。最好诠释这种差别的例子就是想象如果你的后验分布是双峰的,频率学派的方法会去选这两个峰当中较高的那一个对应的值作为他们的最好猜测,而贝叶斯学派则会同时报告这两个值,并给出对应的概率。
- 贝叶斯定理和全概率公式的应用。
**
- 用贝叶斯定理解释“三门问题”。
数据挖掘
- 数据集的划分方式,以及各种数据集的作用。
- 阐述欠拟合和过拟合,并解释产生的原因。
- 常用的模型分类方法,以及其中重要的模型(监督/非监督、参数/非参数等)有哪些。
- 模型中参数和超参数的区别。
- 线性回归模型对误差所做的假设。
- 线性回归模型调优的方法。
- 线性回归模型的优缺点。
- 逻辑回归模型与线性回归模型的异同点。
- 逻辑回归模型中的L1、L2正则解释及其区别。
- 决策树模型选择分支的几种方式及其区别。
- 随机森林预测结果优于决策树的原因。
- 随机森林与GBDT模型的异同点。
- 随机森林、GBDT模型的优缺点。
- XGBoost模型能够有比较好的效果的原因,以及实现并行的原理。
- 针对预测、二分类、多分类常用的模型评估方法。
- 阐述准确率和正确率的区别,以及为什么会选用准确率。
- 用通俗的语言解释准确率和召回率。
- 阐述ROC与AUC的联系。
- 简述混淆矩阵。
以上列举的只是一部分问题,其中每个问题又可以衍生出许多不同的问题。不同于在学校的考试中会比较重视原理以及相关证明,在面试中对知识点的考查,通常是希望候选人对这些知识点能够做到融会贯通,用通俗易懂的语言进行阐述。
比如对准确率和召回率的解释,虽然可以利用定义中的表格和相关概念进行阐述,但是如果能做到融会贯通,利用警察抓小偷的案例进行阐述(将准确率解释为在抓到的人中小偷的占比,将召回率解释为所有小偷被抓到的占比),显然比单纯地背诵概念好得多,既体现出专业性,又体现出自己的思考。
建议:对于这部分内容,一定要和未来的工作场景相结合,这样才能体现出你对它们的真正理解。
二、编程能力考查
不同于基础知识考查,编程能力考查更多的是需要候选人现场进行编程——可能在专门的代码考核程序上进行,也可能直接用纸笔来写代码。所考查的编程语言会根据候选人简历中的内容和岗位而定。
对于数据分析师而言,对R、Python主要考查的是与数据框相关的操作,包括列的增加、删减、汇总以及数据框之间的连接操作等。这部分考查的内容比较直观,而且数据框也是数据分析师在工作中接触最多的对象。另外,也会对比较复杂的循环、函数进行考查,要求候选人完成循环语句或者功能函数,这部分考查结合了统计学的一些知识和逻辑思维。
对SQL则主要考查数据提取和表之间的计算,需要候选人在掌握基本的SQL语句、聚合函数,表连接的同时,着重了解窗口函数以及对数据倾斜的处理方法。窗口函数和数据倾斜被考查到的概率很大。
注意,在编写代码时一定要规范、整齐、注释合理。考查编写代码,一是看候选人对编程是否熟悉;二是看候选人是否有良好的编程习惯,能否遵循一定的规范。有些候选人虽然有丰富的工作经验,但是在编程方面却没有养成良好的习惯,这在面试中也是一个扣分项。
此外,面试官也会对项目中用到的一些包或者函数的细节进行考查,一是看候选人是否真的参与了这些项目;二是看候选人对细节的掌握情况。这就要求候选人要重视项目细节,并且能对项目进行复盘。
三、实战项目考查
实战项目考查主要分两部分:
- 一是对候选人做过的项目进行了解;
- 二是对业务常识进行考查。常见的面试问题如下:
- 简单做自我介绍。
- 阐述之前参与过的某个项目,并且举例说出遇到的困难和解决办法。
- 对于之前做过的项目,还有哪些可进一步提升的地方。
- 近期×××指标有所下降,请针对该问题提出系统化的分析方法。
- 近期产品针对×××功能进行了改版,如何评估改版的效果。
- 公司最近举办了一个营销拉新活动,如何评估这次拉新的效果。
- 在设计数据报表时需要考虑的地方。
- 常用的数据监控方法(如果在此前工作中有所涉及,则可以进行详细阐述)。
- 用户画像的数据来源以及应用场景。
- 针对×××业务,如何运用数据库中的用户画像数据。
- AB测试所运用的数学原理。
- AB测试流量划分的方法,以及最小样本量的计算方法。
- 做分析报告需要注意的点,可以展示之前做过的脱敏后的分析报告。
- 在做数据挖掘模型之前,需要进行哪些可行性分析。
- 特征工程包含的变量处理方法。
- 异常值和缺失值处理的方法。
- 如何评估模型上线后的效果。
- 近期看的书或者学到的新的数据分析方法。
这部分是实战项目考查,在阐述项目时要注意数据导向、流程明确、关注技术细节,对项目从开始构建到上线再到迭代的过程进行系统的梳理。
这就要求候选人在做项目的过程中认真思考,真正理解项目背后的技术细节和业务逻辑,而非简单地完成需求。
关于AB测试、用户画像等知识,可以多看这方面的文章,了解目前业内先进的方法。
上面最后一个问题实际上是考查候选人的潜能、学习能力和态度,只有不断进行学习,才能在未来的工作中始终保持积极的态度,积极探索和掌握新的技术。

