第二讲 统计学模型.pdf
描述性统计：用定量的数据去描述事物特征。

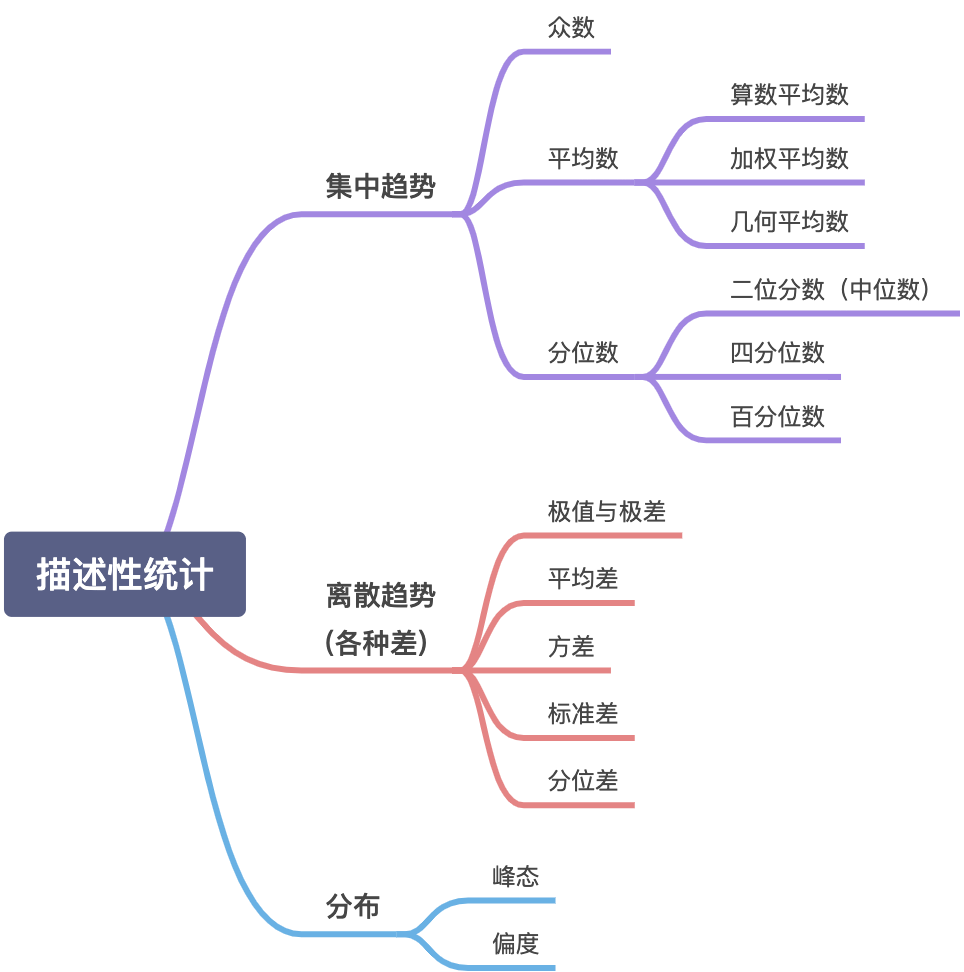
1.集中趋势

平均值的缺点：容易受到极值的影响。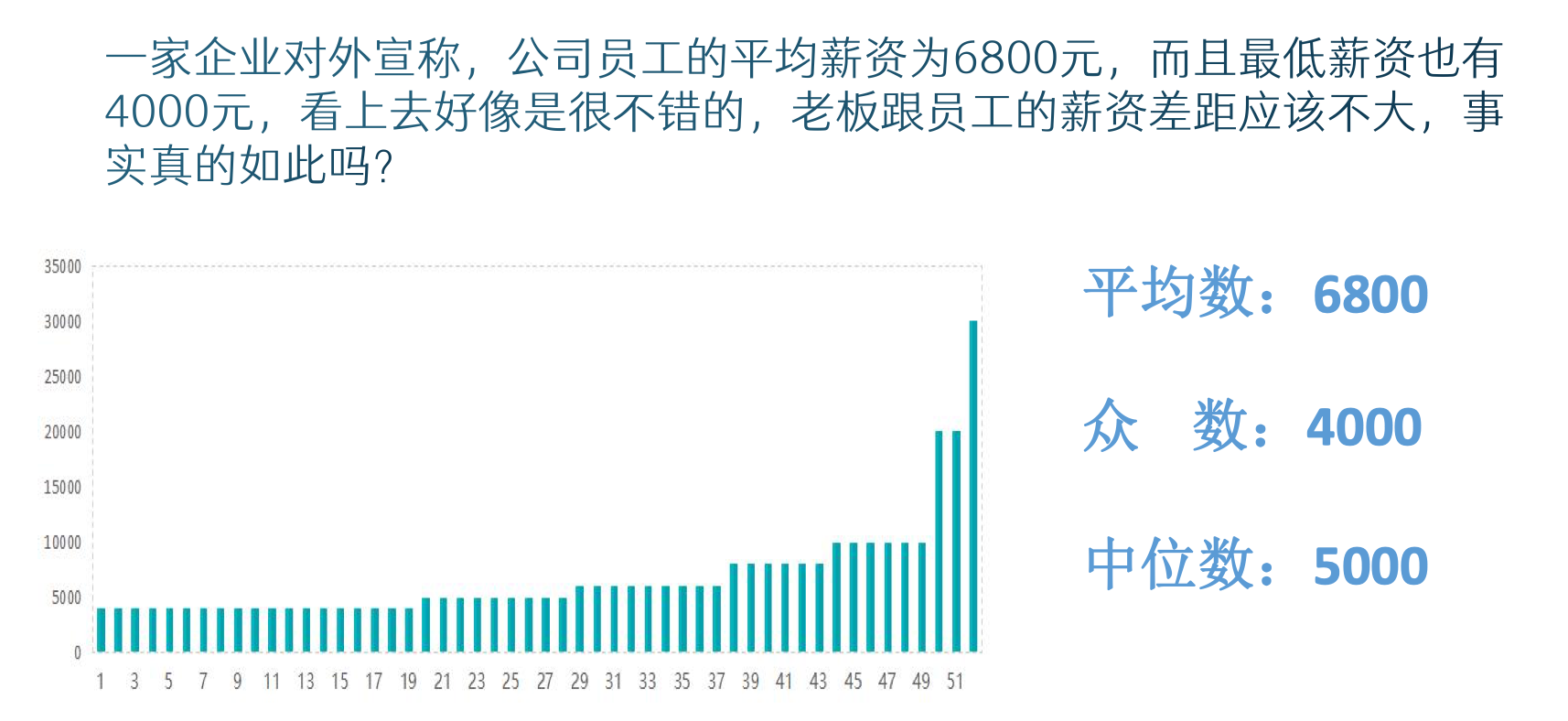

如何解决极值的影响？

• 方法1：使用加权平均数

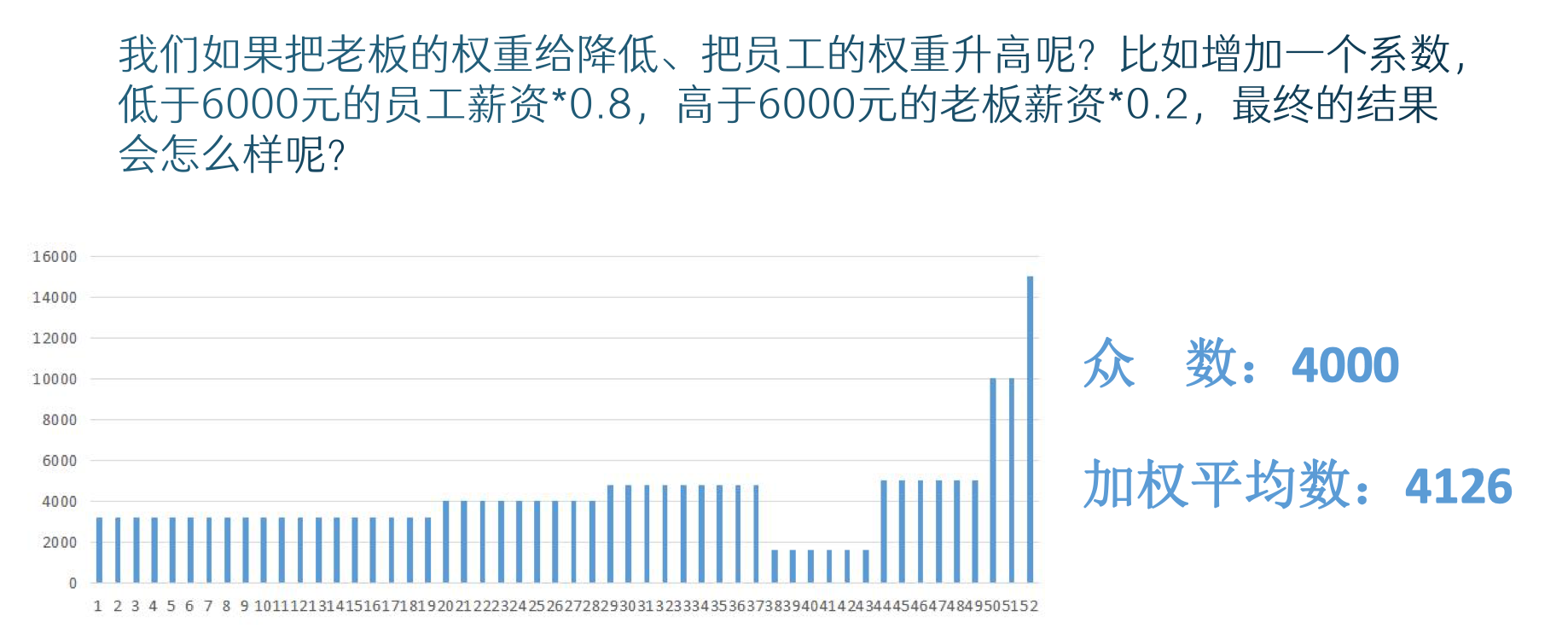
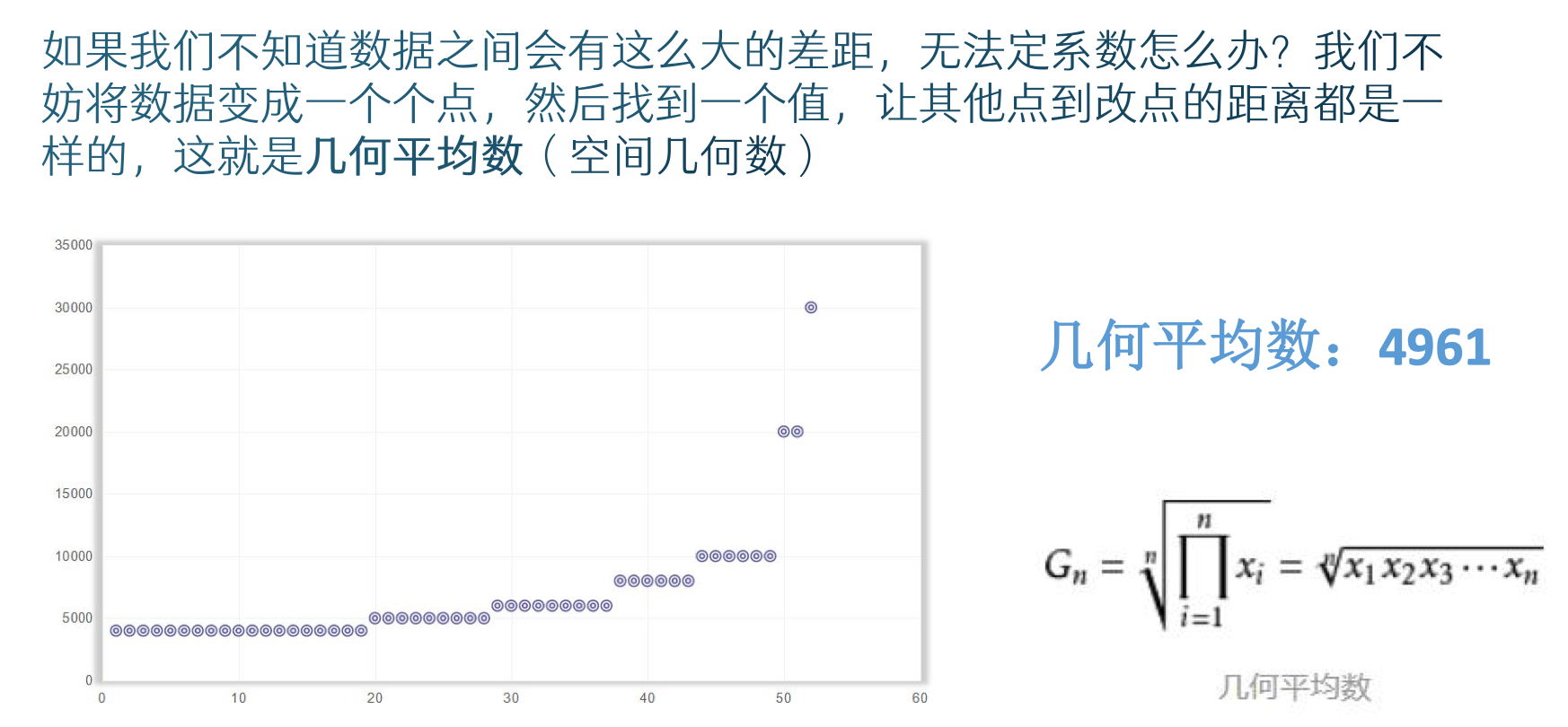
• 方法2：制作散点图，求几何平均数。

2. 离散趋势

• 极值：就是最大值、最小值，代表着数据集合中的上限和下限。
• 极差：极值之差，又称全距，记作R。一般情况下，极差越大，离散程度越大，其值容易受到极端值的影响。极差不能用作比较，单位不同 ，方差能用作比较， 因为都是个比率。
• 平均差：每个值与算数平均数之差的绝对值的算数平均数，即，表征每个数值偏离平均值的程度。
• 方差：将每个值与平均值的偏差进行平方，最后除以总数据量的值，即简单来说就是表示数据与期望值的偏离程度。
• 标准差：方差的平方根，同样也是表示数据与期望值的偏离程度。

• 分位差：是对极差指标的一种改进，就是从变量数列中剔除了一部分极端值之后重新计算的类似于极差的指标。常用的分位差有四分位差、八分位差、十分位差、十六分位差、三十二分位差以及百分位差。

  • 四分位差：它是上四分位数（Q3，即位于75%）与下四分位数（Q1，即位于25%）的差。四分位差反映了中间50%数据的离散程度，其数值越小，说明中间的数据越集中；其数值越大，说明中间的数据越分散。四分位差不受极值的影响。

    3. 分布

    

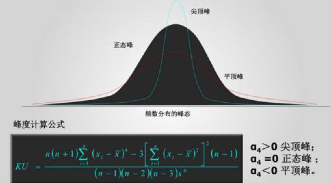
• 峰度：表征概率密度分布曲线在平均值处峰值高低的特征值。

  • 当峰度=0时，分布和正态分布基本一致；
  • 当峰度>0时，分布形态纤瘦高狭；
  • 当峰度<0时，分布形态扁平低阔。

• 偏度：偏态系数以平均值与中位数之差对标准差之比率来衡量偏斜的程度。
  • 偏度<0，是左偏、负偏，此时，均值<中位数<众数
  • 偏度>0，是右偏、正偏，此时，均值>中位数>众数

（考点）在不同的分布中，中位数、期望(均值)、众数三者的大小关系：**

• 正态分布：中位数=期望=众数。
• 正偏态分布（图形尾巴在右侧）：期望>中位数>众数。
• 负偏态分布（图形尾巴在左侧）：期望<中位数<众数

  记忆技巧：期望离尾巴近，中位数在中间，剩下的位置就是众数。