1. 什么是误差消减比例

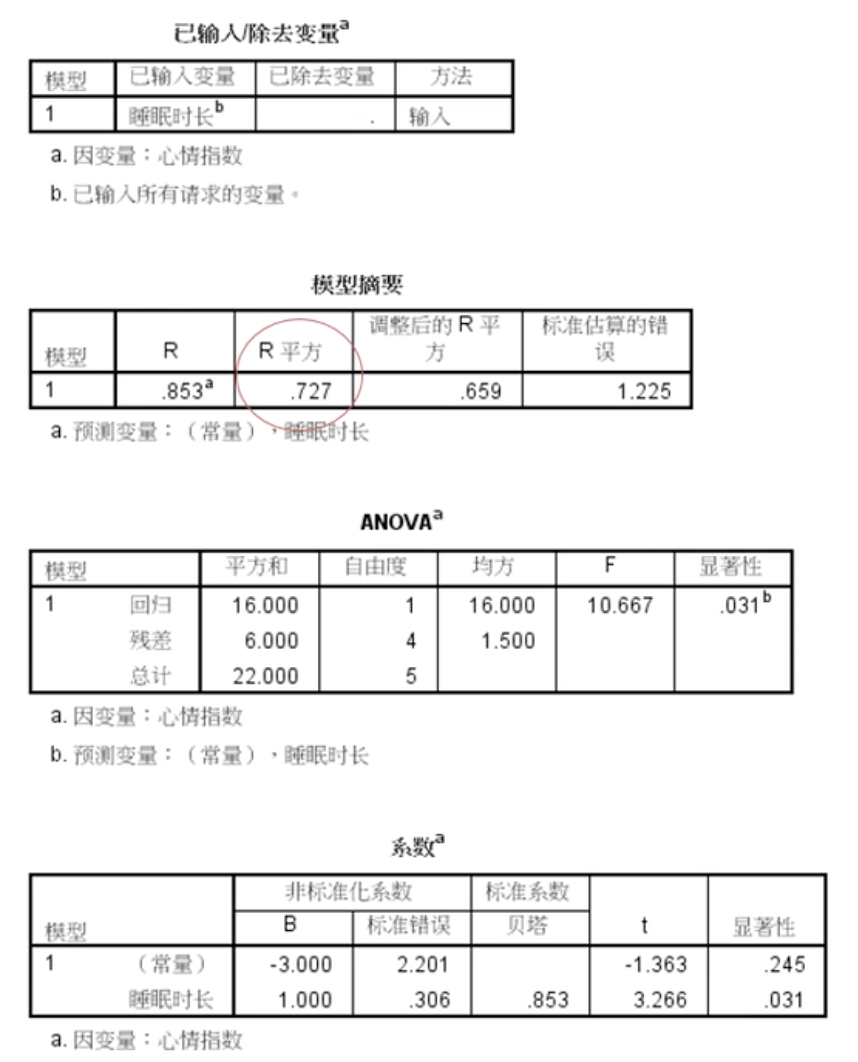
上图中的R就是误差消减比例（PRE，proportional reduction in error）
用途

• 评估回归模型的预测力

• 模型能解释因变量方差的百分比

  2. 案例

  自变量：学校0=A大学，1=B大学
  因变量：收入（单位：千元）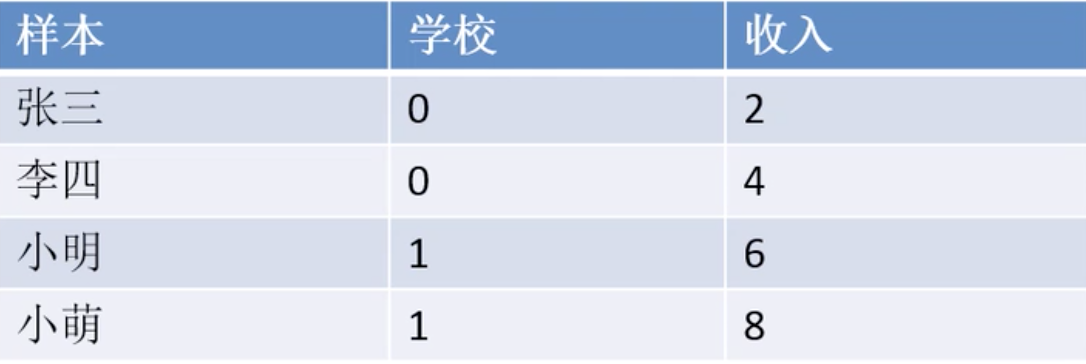
  
  假设，不知道学校信息，只知道收入的均值。我们可以根据收入的均值进行预测，他们的收入均值为5（千元）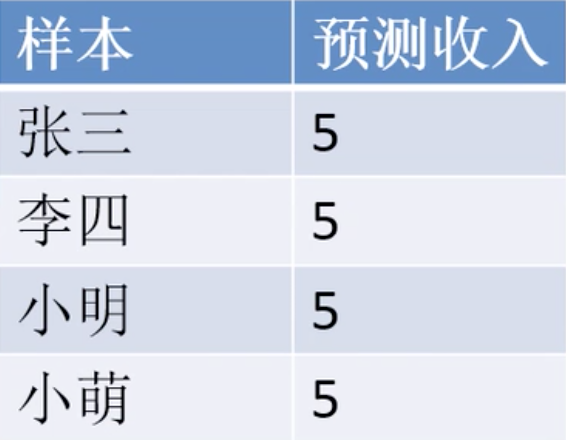
  
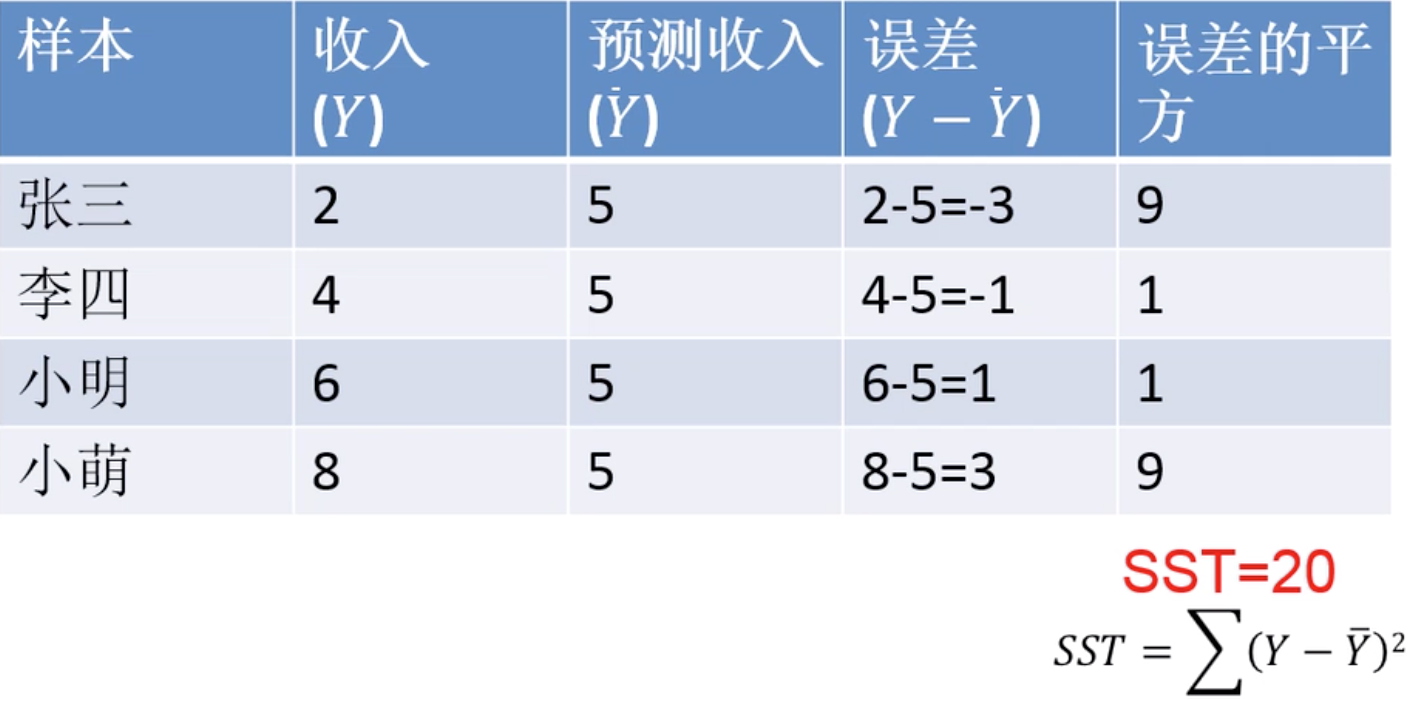  SST叫做总体平方和
  当我们知道了学校的信息，看看牙据此拟合一条回归直线：
  据此，当x=0时，收入为3，当x=1时，收入为7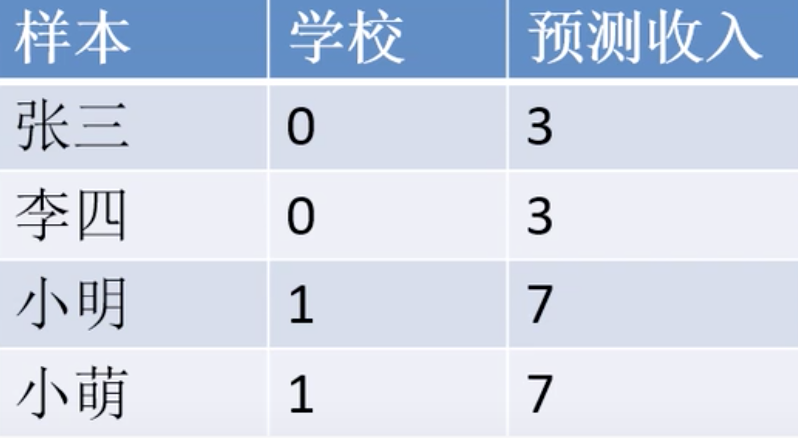
  
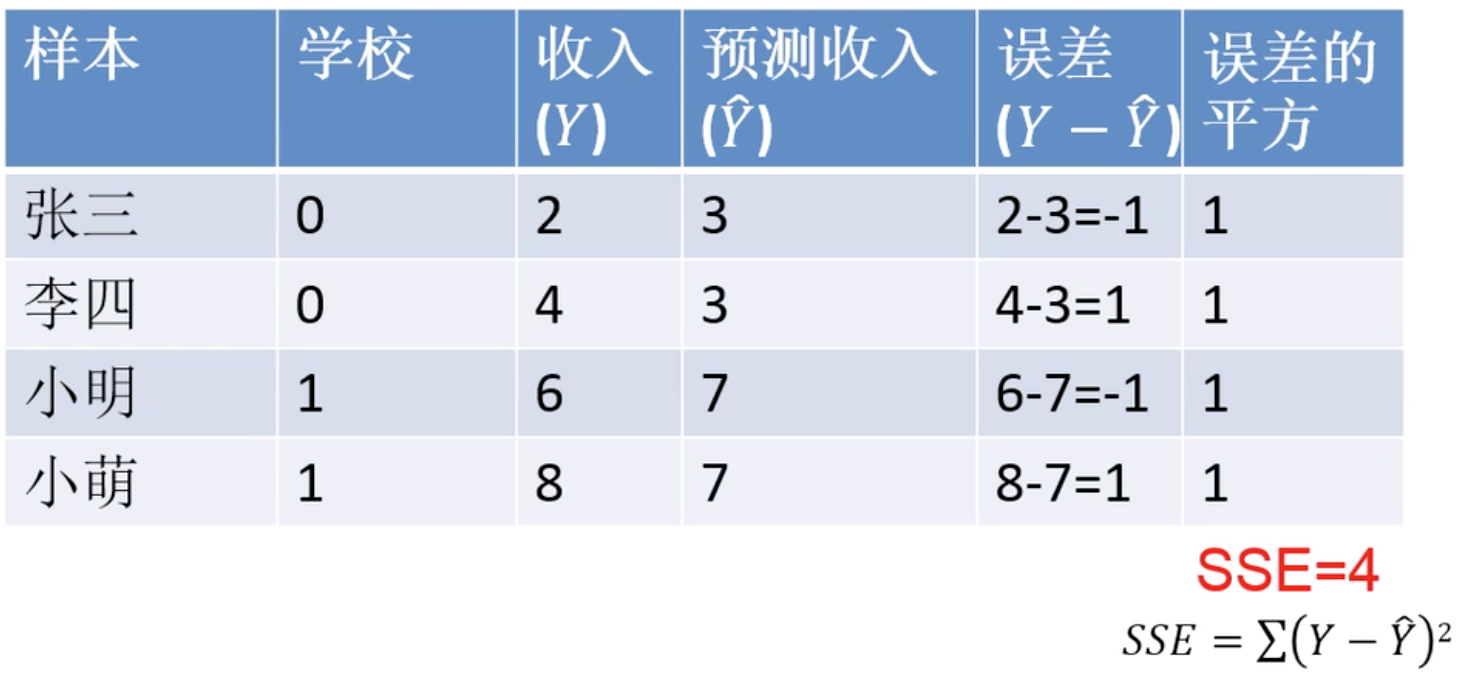  SSE叫做残差（误差）平方和
  综上，

• 如果我们不知道学校，误差的平方和(SST)=20

• 在知道了学校后，可以拟合一条回归直线，误差的平方和(SSE)=4
• 减少了16(SSR)是回归直线x的功劳，知道了x帮我们减少了16/20=80%的预测误差

SSR=16还可以怎么计算？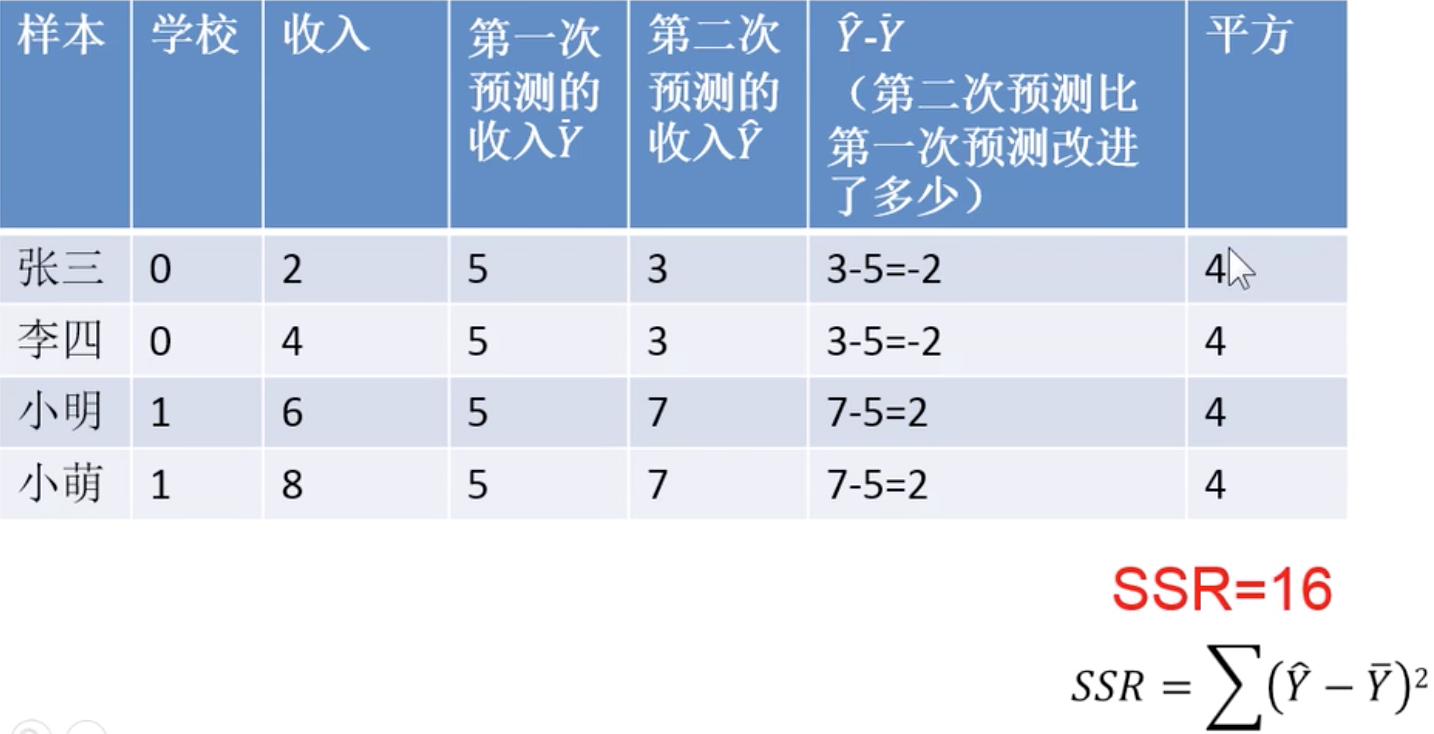



SSR/SST就是误差消减比例

总结：

• 总体平方和SStotal（SST）：
• 误差平方和（或残差平方和）SSerror（SSE），Y的变异中不可以被回归直线所解释的部分：
• 回归平方和（或解释平方和）SSreg（SSR），Y的变异中可以被回归直线所解释的部分：
• 由于SST=SSE+SSR，因此误差消减比例：PRE=SSR/SST=1-SSE/SST

案例中**

• PRE=SSR/SST=16/20=80%
• PRE=1-SSE/SST=1-4/20=1-20%=80%

说明收入的方差（或变异）中有80%被学校解释了。
注：在实际情况中，PRE很少高于50%