本文大纲 2.2 统计学模型—聚类模型 - 图1

分类与聚类

  • 分类：已经知道了分类标准和规则

  • 聚类：根据数据本身的特性研究分类方法，并遵循这个分类方法对数据进行合理的分类，最终将相似数据分为一组，也就是“同类相同、异类相异”

怎么进行聚类？

案例：某公司旗下共有A-H8款汽车类型，每款汽车的销量与利润各不相同，公司为了升级业务，需要将这几款汽车分为两类，我们应该怎么做呢?

本题使用k-means方法进行聚类

销量 利润
A 0 0
B 1 2
C 4 3
D 4 4
E 5 7
F 6 8
G 7 7
H 9 5
  • 第一步：确定分组数

本题设K=2

  • 第二步：随机选K个值为数据中心

选择A、B两个点为初始中心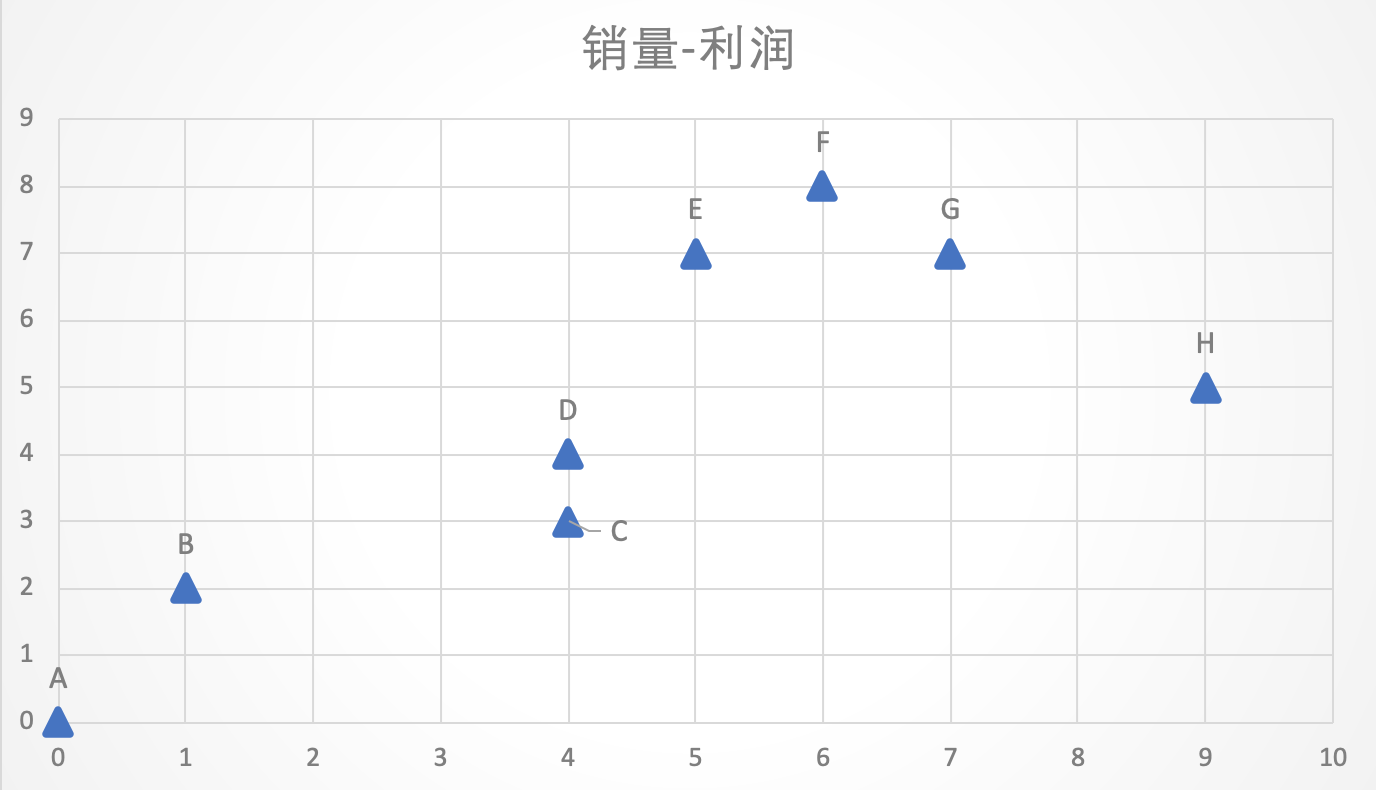
image.png

  • 第三步：其他数值与数据中心的距离（欧氏距离） | | 距离A的距离 | 距离B的距离 | | :—-: | :—-: | :—-: | | C | 5.0 | 3.2 | | D | 5.7 | 3.6 | | E | 8.6 | 6.4 | | F | 10.0 | 7.8 | | G | 9.9 | 7.8 | | H | 10.3 | 8.5 |

    • 第一组（离A最近的点）：A
    • 第二组（离B最近的点）：B、C、D、E、F、G、H
  • 第四步：重新选择数据中心
    • 第一组只有A，所以A仍是数据中心；
    • 第二组有7个值，计算平均坐标为（5.14, 5.14）

image.png

  • 第五步：重复第三步，计算所有点距离数据中心的距离 | | 距离A的距离 | 距离P的距离 | | :—-: | :—-: | :—-: | | B | 2.2 | 5.2 | | C | 5.0 | 2.4 | | D | 5.7 | 1.6 | | E | 8.6 | 1.9 | | F | 10.0 | 3.0 | | G | 9.9 | 2.6 | | H | 10.3 | 3.9 |

    • 第一组（距离A点最近的点）：A、B
    • 第二组（距离P点更近的点）：C、D、E、F、G、H
  • 第六步：再次重新选择数据中心
    • 第一组的平均坐标为O(0.5, 1)
    • 第二组的平均坐标为Q(5.83, 5.67)

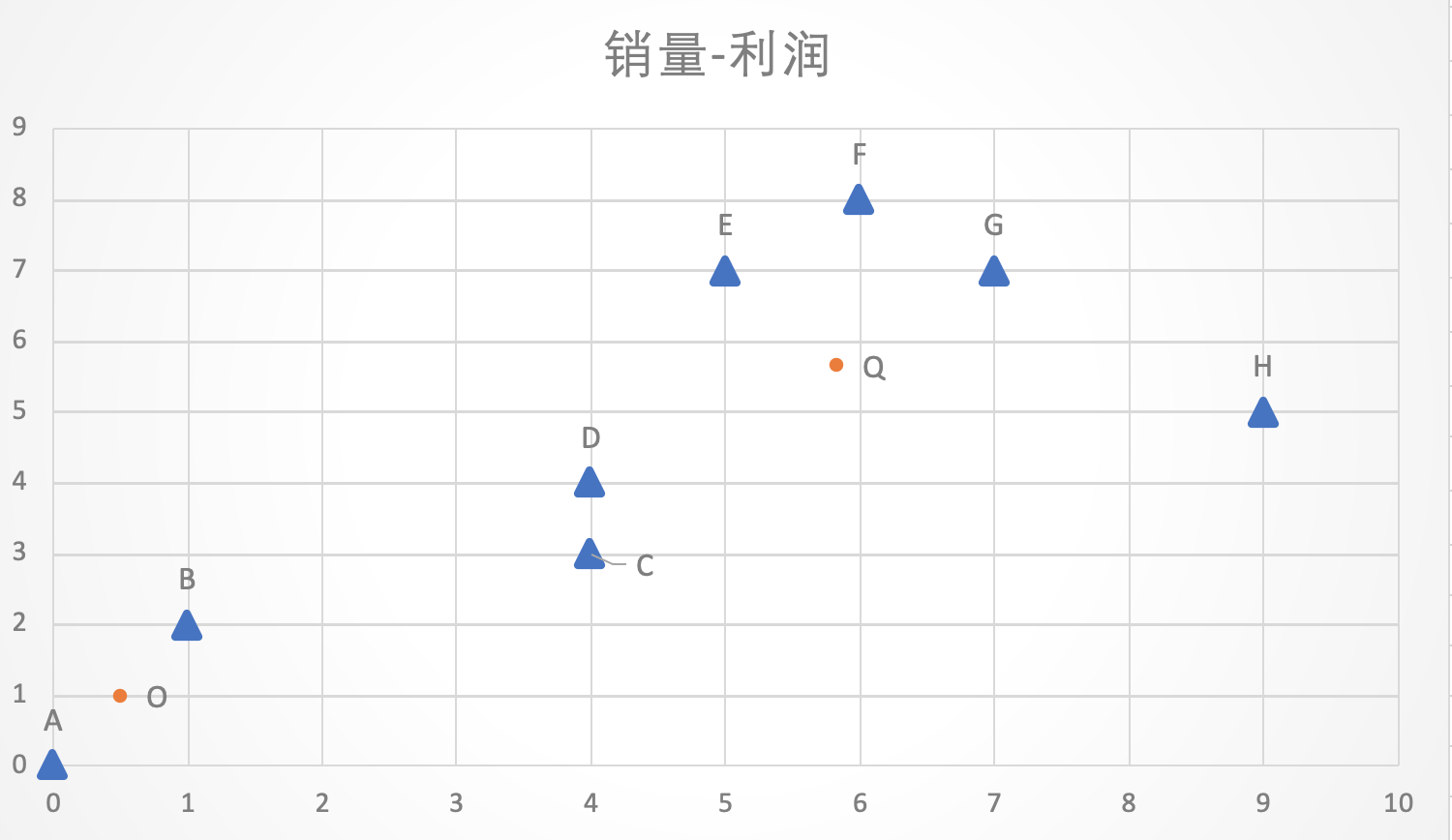
image.png

  • 第七步：再次计算所有点到数据中心的距离 | | 距离O的距离 | 距离Q的距离 | | :—-: | :—-: | :—-: | | A | 1.1 | 8.1 | | B | 1.1 | 6.1 | | C | 4.0 | 3.2 | | D | 4.6 | 2.5 | | E | 7.5 | 1.6 | | F | 8.9 | 2.3 | | G | 8.8 | 1.8 | | H | 9.4 | 3.2 |

    • 第一组（距离O点最近的点）：A、B
    • 第二组（距离Q点更近的点）：C、D、E、F、G、H

与上次的分组情况一样，说明聚类计算已达到极限

所以聚类分组的结果是：

  • 第一组：A、B
  • 第二组：C、D、E、F、G、H

总结：k-means聚类的算法是

  • 确定分组数k
  • 随机选择k个数据中心，计算其他点到数据中心的欧氏距离，并分组
  • 计算每个分组的平均坐标，作为新的数据中心，计算欧氏距离，分组……
  • 直至穷尽分组，得到的结果就是聚类分组